δ関数（読み）デルタかんすう（英語表記）δ function

改訂新版　世界大百科事典

δ関数 (デルタかんすう)
δ function

1920年代に物理学者P.A.M.ディラックは，次のような関数δ（x）を導入して形式的な計算を行い，量子力学の研究に有効に利用した。すなわち，実数xの関数δ（x）とは，x≠0のときδ（x）＝0，x＝0のときδ（0）＝∞で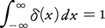，なるものとし，（－∞，∞）で連続な任意の関数φ（x）に対して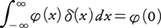，あるいは，より一般に任意の実数cについて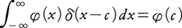，が成り立つとした。このδ（x）をディラックのδ関数，または単にδ関数と呼ぶ。このような関数は数学的にふつうの意味の関数としては認められないものであるが，1940年代後半に，フランスの数学者シュバルツL.Schwartz（1915-2002）によって創始された超関数の理論により，厳密な数学的意味づけが与えられた。それによると，（－∞，∞）で無限回微分可能で，ある有界集合の外ではφ（x）≡0となる関数φの全体をとするとき，δ関数は任意のφ∈に対してT_δ（φ）＝φ（0）で定義される汎関数T_δである。これは直観的にはx＝0における質量1の質点と考えることができるが，また次のような関数列｛f_n｝，あるいは｛g_n｝の，ある意味での極限としても与えられる。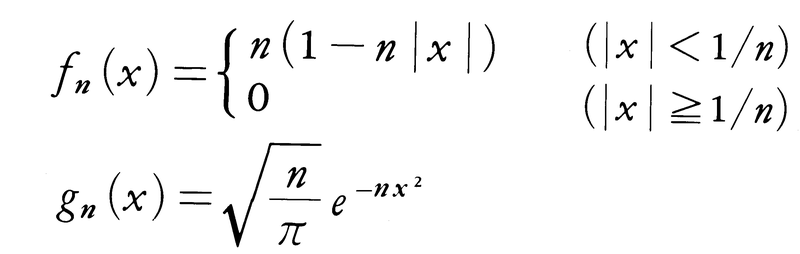

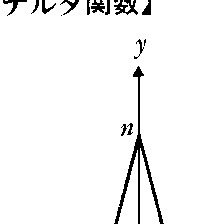
これらの関数はすべて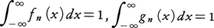を満たしながら，図に示すように，nが大きくなるに従ってその重みがx＝0の近くへしだいに集中していくので，上に述べた直観的解釈に合致する。なお，ディラックは次のヘビサイド関数，

　Y（x）＝1（x≧0），Y（x）＝0（x＜0）

の導関数がδ（x）であるとし，さらにδ（x）の導関数δ′（x），δ″（x），……をも扱ったが，これらも超関数の理論によってすべて数学的に厳密に意味づけられた。
→超関数
執筆者：伊藤 清三

図－δ関数

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

δ関数
デルタかんすう
δ-function

量子力学を定式化するために，P.A.M.ディラックが導入した関数。 x≠0 のとき δ(x)＝0 であるにもかかわらず，x＝0 の点を含む任意の領域での積分が
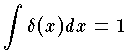を満足するような関数 δ(x) のことをいう。あるいは，x＝0 で連続な任意の関数 f(x) に対して，
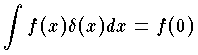を満足する関数と定義してもよい。ただし，積分領域は x＝0 を含んでいれば任意でよい。 δ(x) は x＝0 で強い特異性をもつから，通常の関数とはいえないが，数学的には超関数として厳密な基礎づけがなされている。 δ(x) は， sin gx/πx という関数の g→∞ の極限として表わすこともできる。 δ(x) の定義によって，δ(－x)＝δ(x) となるから δ(x) は偶関数，また δ'(－x)＝－δ'(x) となるから δ'(x) は奇関数である。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のδ関数の言及

【演算子法】より

…関数に対する微分や積分の演算を記号的，あるいは代数的に行い，微分方程式を形式的に解く手法を演算子法という。19世紀の終りころに，イギリスの工学者O.ヘビサイドが電気工学におけるいろいろな現象を記述する常微分方程式や，電信方程式と呼ばれる偏微分方程式を解くのにこの手法で成功をおさめて以来，演算子法はまとまった一つの理論となった。しかし，彼の議論は数学の対象としうるほどの厳密さを備えていなかった。その後，ラプラス変換や超関数などによる裏づけがなされてしだいに体系を整えてきた。…

※「δ関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」