ホモトピー（その他表記）homotopy

改訂新版　世界大百科事典

ホモトピー
homotopy

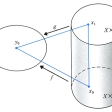
位相空間Xから位相空間Yへの二つの連続写像f，f′：X→Yに対し，Xと閉区間［0，1］の直積X×［0，1］からYへの連続写像F：X×［0，1］→Yであって，Xのどの点xについてもF（x，0）＝f（x），F（x，1）＝f′（x）となるものがとれるとき，fとf′は同じホモトピー類に属する，またはfとf′はホモトープであるという（図）。f_t：X→Y（0≦t≦1）をf_t（x）＝F（x，t）で定義すれば，各f_tは連続写像で，｛f_t｝はtに関して連続的に変わる。したがってfとf′が同じホモトピー類に属するとはfからf′に連続的に変形できることを意味している。二つの位相空間X，Yに対し，連続写像f：X→Yと連続写像g：Y→Xをとって，合成g◦f：X→X，f◦g：Y→YがそれぞれX，Y上の恒等写像と同じホモトピー類にあるようにできるとき，XとYは同じホモトピー型であるという。同相な位相空間は同じホモトピー型であるが，同相でなくとも同じホモトピー型となることがある。例えば，線分，円板，球体は1点と同じホモトピー型をもち，円柱，メービウスの帯，中心を除いた円板は円周と同じホモトピー型をもつ。ホモトピー類やホモトピー型の研究は位相幾何学の重要な分野で，1920年ころよりその研究が始まったが，50年以後にめざましく進展し，また多様体の問題などに応用されて多くの問題が解かれた。
執筆者：中岡 稔

図－ホモトピー

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ホモトピー
ほもとぴー
homotopy

ホモトピーは、ホモロジー理論と並んで、組合せおよび代数的トポロジーにおける基本的な概念である。

　20世紀初頭にトポロジーの創始者であるポアンカレは、ホモロジー群とともに位相空間の基本群を定めたが、これを一般化したものがホモトピーである。

　X、Yが位相空間でx₀、y₀がそれぞれそれらの一点とする。点x₀をy₀へ写す（連続）写像fとgがホモトピックであるとは、Xと単位区間との直積空間からYへの連続写像
　　F:X×［0,1］→Y
が存在して
　　F(x,0)=f(x),　F(x,1)=g(x),
　　F(x₀,t)=y₀　0≦t≦1
となることである。ホモトピックの関係で写像を分類した同値類をホモトピー類という。とくにXとしてn次元球面をとるとき、このホモトピー類は群をなし、位相空間Xのn次元ホモトピー群π_n(X)とよばれる。n≧2のときこれはアーベル群となり、n=1のときπ₁(X)が基本群である。基本群が単位元のみである空間は単連結であるという。n(≧2)次元球面は単連結であるが、円周はπ₁(S¹)=Z（整数の群）であるので単連結ではない。さらにXもYもn次元球面のとき、すなわちn次元球面のn次元ホモトピー群は、直観的にXがYの上に何回巻き付いているかというようすを示す整数である写像度で与えられる。すなわち
　　π_n(Sⁿ)=Z　（整数の加法群）
となる。

［野口　廣］

[参照項目] | トポロジー | ホモロジー

ホモトピー

出典　小学館　日本大百科全書(ニッポニカ)