日本大百科全書(ニッポニカ) 「エルミート行列」の意味・わかりやすい解説
エルミート行列
えるみーとぎょうれつ
正方行列Aがその随伴行列*Aに等しいとき、つまりA=*Aであるとき、フランスの数学者エルミートの名をとり、Aをエルミート行列という。ここで、随伴行列とは、転置行列(行と列とを入れ換えた行列)の成分の複素数を共役複素数に置き換えたものをいう。たとえば、二次正方行列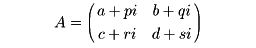
に対して、随伴行列は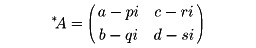
である。
実エルミート行列は対称行列(主対角線に関して対称な位置にある二つの要素がそれぞれ等しい行列)にほかならない。
n次列ベクトル全体Cnのつくる線形空間の内積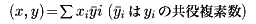
とn次正方行列Aとに、
(Ax,y)=(x,*Ay) (x,y∈Cn)
という関係がある。これを用いてエルミート行列Aは
(Ax,y)=(x,Ay) (x,y∈Cn)
を満たす正方行列Aと定義してもよい。
一般にA*A=*AAを満たす正方行列Aを正規行列という。エルミート行列はユニタリー行列(複素内積を変えない行列)とともに正規行列の重要な例になっている。また、正方行列Aが正規行列であるための必要十分条件は、U-1AUが対角行列(主対角線外の成分がすべてゼロとなる行列)になるようなユニタリー行列Uがあることであるから、エルミート行列Aは、ユニタリー行列UでU-1AUを対角行列にすることができる。
エルミート行列は、固有値がすべて実数となる正規行列であると定義してもよい。とくに、エルミート行列の固有値がすべて正、非負、負、非正に従い、それぞれ、正値、半正値、負値、半負値エルミート行列という。エルミート行列A=(aij)i,j=1,……,nに対し、
Ak=(aij)i,j=1,……,k (k=1,……,n)
とすると、Aが正値または負値であるためには、それぞれ、
detAk>0または(-1)kdetAk>0
(k=1,……,n)
であることが必要十分条件である。ここでdetAkはAkの行列式を表す。
[菅野恒雄]


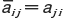 (
(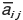 は aji の共役複素数)がいえれば,行列 H をエルミート行列と呼ぶ。たとえば
は aji の共役複素数)がいえれば,行列 H をエルミート行列と呼ぶ。たとえば 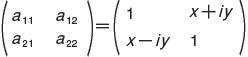 はエルミート行列となる。つまり,
はエルミート行列となる。つまり,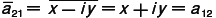 ,
,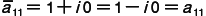 ,
,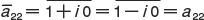 となり,すべての i,j について,
となり,すべての i,j について,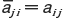 が成り立つからである。この例からもわかるように,エルミート行列では,左上から
が成り立つからである。この例からもわかるように,エルミート行列では,左上から