共役（読み）きょうやく（英語表記）conjugate

ブリタニカ国際大百科事典 小項目事典

共軛とも書く。対になっていること，あるいは対になって結合することをいうが，数学では，それぞれの場合に特別の意味をもって使用される。(1) 共役直径 c.diameters　楕円あるいは双曲線の，一つの直径に平行な弦の中点の軌跡はまた，これらの楕円あるいは双曲線の，他の直径となる。この二つの直径は共役であるといい，一方を他方の共役直径，あるいは単に共役径という。(2) 共役軸 c.axis　双曲線 x²/a²－y²/b²＝1 において，y 軸はこの曲線と交わらない。このように双曲線の二つの対称軸のうち，曲線と交わらない軸を共役軸という。(3) 共役双曲線 c.hyperbola　二つの双曲線 x²/a²－y²/b²＝1 と x²/a²－y²/b²＝－1 とは，互いに共役な双曲線であるという。これらの漸近線は一致する。(4) 共役な極 c.poles　二次曲線（または二次曲面）には，点 Pの極線（または極平面）が点 P'を通れば，P'の極線（または平面）も Pを通るという性質がある（→極線と極点）。このような関係にある 2点 P，P'はこの二次曲線（または二次曲面）に関して共役であるという。(5) 共役な極線（極平面） c.polars　二次曲線（または二次曲面）には，直線（平面）p の極 Pが p'の上にあれば，p'の極 P'も p の上にあるという性質がある。このような関係にある 2直線（平面）p，p'は，この二次曲線（二次曲面）に関して共役であるという。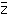(6) 共役複素数　z＝x＋yi（x，y は実数）に対して，複素数 ＝x－yi を共役複素数という。幾何学的には，ガウス平面上で，z と 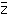とは x軸に関して，対称である。z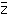＝ となる数は実数だけである。(7) 共役四元数 c.quateernion　二つの四元数 q＝x₀＋x₁i＋x₂j＋x₃k と 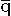＝x₀－x₁i－x₂j－x₃k（i，j，k は虚数）は，互いに共役であるという。(8) 共役根 c.roots　実係数の方程式が虚根 a＋bi（a，b は実数，b≠0）をもてば，必ずその共役複素数 a－bi もこの方程式の根となる。このように互いに共役複素数となっているような 2根を共役根という。(9) 共役部分群 c.subgroup　群 G の部分群を H とし，a を G の任意の元とするとき，集合 a^-1Ha＝｛a^-1ha｜h∈H｝を考えれば，a^-1Ha もまた G の部分群である。これを H の共役部分群という。G の任意の元 a に対して，a^-1Ha＝H が成り立てば，H は G の正規部分群，あるいは不変部分群といわれる（a^-1 は a の逆元）。(10) 共役体 c.fields　体 K の二つの拡大体を K₁，K₂ とするとき，K₁ を K₂ の上へ写像する対応σが存在し，K の任意の元αに対して，σ（α）＝αが成り立てば，K₂ を K に関する K₁ の共役体という。(11) 共役元 c.elements　体 K の拡大体 K'の 2元α₁，α₂が，ともに K に関する代数的元であって，K における同一の既約多項式 f（x）の根となっているとき，このα₁，α₂を K に関する共役元という。

有機化合物で，2個以上の多重結合，すなわち二重結合や三重結合が1個の単結合をはさんで存在し，これらの結合が相互作用を示すこと。この相互作用は電子の非局在化に基づくもので，不飽和結合にはさまれた単結合はある程度不飽和結合の性質を示す。たとえばブタジエン CH₂＝CH－CH＝CH₂ における原子間距離はC＝Cで 1.37Å，C－Cで 1.47Åであり，前者はエチレンのC＝Cの 1.34Åより長く，後者はエタンのC－Cの 1.54Åより短い。これは共役による相互作用の結果であり，不飽和結合に関与するπ電子の広がりがあると考えると説明がつく。共役はその物質の光の吸収のような物理的性質にも，付加反応性のような化学的性質にも影響を及ぼす。 (→共役二重結合 )

出典　ブリタニカ国際大百科事典 小項目事典

デジタル大辞泉

１ 数学で、二つの角・線・点・図形・数などが互いに対称的あるいは相補的関係にあり、入れ換えてもその関係に変化のないこと。
２ 環状構造をもつ不飽和化合物において二重結合が交互に存在すること。

出典　小学館

世界大百科事典内の共役の言及

【双曲線】より

…定数を2aとし，線分FF′の長さを2cとするとき，e＝c/a(＞1)を離心率という。直線FF′を横軸，線分FF′の垂直2等分線を共役軸といい，これらを合わせて主軸という。また，線分FF′の中点を中心という。…

※「共役」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社