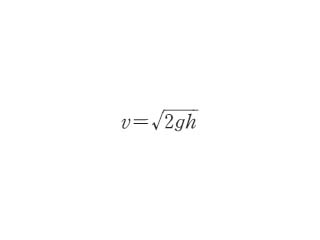トリチェリの定理
とりちぇりのていり
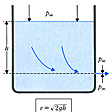
器に液体を入れ、器の壁に穴をあける。穴は容器の大きさに比べ十分小さいとすると、流れは定常状態としてよい。このとき穴から流れ出す液体の速さvは、
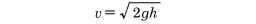
で表される。これをトリチェリの定理という(図)。ここでgは重力加速度9.8m/s2、hは水面から穴までの深さである。トリチェリの定理はベルヌーイの定理
P+(1/2)ρv2+ρgz=一定
を用いると証明できる(ρは液体の密度)。穴の位置をz=0にとると、水面の高さはz=hの位置にあり、容器が十分大きいため水面の下がる速度はゼロと置ける。穴の位置および水面にかかる圧力はともに大気圧p∞に等しい。したがって、
P∞+ρgh=P∞+(1/2)ρv2
の等式が成り立ち、穴から流れ出す液体の速度が
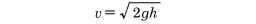
と求められる。
[池内 了]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
トリチェリの定理 (トリチェリのていり)
Torricelli's theorem
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
百科事典マイペディア
「トリチェリの定理」の意味・わかりやすい解説
トリチェリの定理【トリチェリのていり】
〈容器に入れた粘性の小さい液体が小さい穴から流れ出るとき,流出速度は(式1)に等しい(gは重力加速度,hは穴から液面までの高さ)〉。つまり流出速度は,質点がhの高さから自由落下するとき得る速度に等しい。ベルヌーイの定理から容易に導出される。→トリチェリ/トリチェリの真空/トル
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
トリチェリの定理
トリチェリのていり
Torricelli's theorem
容器の中の液体が,壁にあけた小さな穴から流出するとき,液体の粘性を無視すれば,流出速度の大きさは 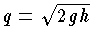 ( g は重力加速度,h は穴から液面までの高さ) で与えられる。これをトリチェリの定理という。この q の値は,物体の自由落下速度に等しく,また,液体の流出方向には依存しない。
( g は重力加速度,h は穴から液面までの高さ) で与えられる。これをトリチェリの定理という。この q の値は,物体の自由落下速度に等しく,また,液体の流出方向には依存しない。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
法則の辞典
「トリチェリの定理」の解説
トリチェリの定理【Torricelli's theorem】
液体が十分に大きな容器の下方(または側方)の孔から流出する際に,流出速度 v はほぼ次の式で与えられる.
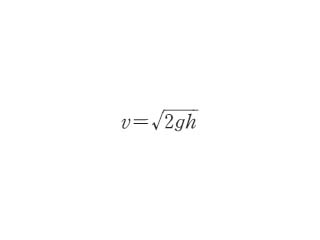
出典 朝倉書店法則の辞典について 情報
Sponserd by 
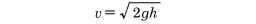
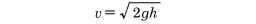


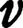
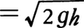 で与えられる。これは
で与えられる。これは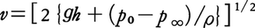 となる。ここでρは液体の密度である。
となる。ここでρは液体の密度である。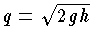 ( g は重力加速度,h は穴から液面までの高さ) で与えられる。これをトリチェリの定理という。この q の値は,
( g は重力加速度,h は穴から液面までの高さ) で与えられる。これをトリチェリの定理という。この q の値は,