重力（読み）ジュウリョク（英語表記）gravity

デジタル大辞泉

じゅう‐りょく〔ヂユウ‐〕【重力】

地球上の物体が地球から受ける引力で、物体の重さの原因となっている力。地球の万有引力と地球自転による遠心力との合力。
[類語]力・パワー・引力・万有引力・斥力・無重力・無重量・揚力・浮力・動力・推力・惰力・弾力・表面張力・向心力・求心力・遠心力・水力・火力・風力・原子力・電力・磁力

出典　小学館

精選版 日本国語大辞典

じゅう‐りょくヂュウ‥【重力】

1. 〘 名詞 〙
2. ① 大きな力。
   1. [初出の実例]「渥美の起んとする胸の上へ非常の重力(ヂウリョク)に速力を加へて〈略〉不意に浪と共に衝当れば」(出典：内地雑居未来之夢（1886）〈坪内逍遙〉一三)
   2. [その他の文献]〔史記‐張儀伝〕
3. ② ( [オランダ語] Zwaartekracht の訳語 ) 地球上の物体が地球による万有引力によって引かれる力。厳密には地球との間に働く引力と、地球の自転による遠心力との合力。ちょうりょく。
   1. [初出の実例]「重力は大地の万物を引に起るものなり。大地能万物を引のみならず、万物亦能大地を引く」(出典：暦象新書（1798‐1802）中)

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

重力
じゅうりょく
gravity

地上で物体を地球に引く力として認識された基本力の一つ。

ニュートンの重力

1665年、ニュートンは、地上の物体の重さを決めている力と天体の間に働く力とが同じであることを発見した。ニュートンによりみいだされた重力の法則は「二つの物体（球）の間に働く力は引力であって、その大きさは両物体の質量に比例し、距離の2乗に反比例する」と表される。この力はすべての物体の間に働くので万有引力ともよばれる。

　いま、二つの物体の質量をm、Mとし、距離をrとすると、重力の強さFはF＝GMm/r²となる。ここでGはニュートンの重力定数とよばれ、G＝6.67×10^-11Nm²/kg²である。距離が物体の大きさに比べて十分に大きくない場合は、力の大きさは前式の関係からずれてくる。一般の物体の重力を求める研究は、19世紀の数理物理学によって達成された。この段階で、重力場という概念が新しく導入され、物質が源となって重力の場を発生させ、他の物体はその重力場と作用することによって力を受けるという見方もされるようになった。質量の間に直接に力が働くという見方を遠隔作用論といい、重力場を通して力が働くという見方を近接作用論という。

［佐藤文隆］

アインシュタインの一般相対性理論

1905年、アインシュタインによる電磁気学についての相対性理論が完成し、重力についても近接作用の見方による重力理論が必要となった。このようにしてニュートンの重力理論を含む、より一般的な理論の研究が出発した。1915年、アインシュタインによる一般相対性理論の提唱は、このような試みの最初の成果であった。この理論は、量子論的効果が重要でない古典的現象に対しては正確に適合することが種々の実験で検証されている。しかし、微視的あるいは超高エネルギー現象における重力現象は、アインシュタインの一般相対性理論だけでは不十分であると考えられている。

　現代の物理学は、重力、電磁気力、さらに原子核・素粒子現象で発見された強い相互作用、弱い相互作用の四つの基本的な力を認識している。そしてこれらの力を統一する試みがなされており、一部は成功している。新しい重力理論はこうした統一理論（統一場理論）の完成のなかで発見されると考えられている。

［佐藤文隆］

重力質量と慣性質量

相対論的な近接作用の見方によれば、重力場を発生させる源、あるいは重力場と作用する結合係数の大きさとしての質量がある。この意味での質量を重力質量という。これは電場が電荷によって発生し、電場との作用がやはり電荷で決まるのと同じ見方である。相対論によれば質量はエネルギーと等価であるため、重力は光のような質量がゼロの粒子によっても生じるし、光は重力の作用をも受ける。

　質量のもう一つの意味は、一般に力を受けた場合、どんな加速度で動きだすかを決める慣性質量、つまり（力）＝（慣性質量）×（加速度）という場合におけるものである。この慣性質量は、重力とは直接に関係していないように思えるが、どの物体についても重力質量と慣性質量の比が一定であるため、重力質量と慣性質量は同一のものとみなすことができる。これは慣性力と重力がまったく等価なものであるという考えを導き、この等価原理は一般相対性理論の根拠の一つとされている。

［佐藤文隆］

無重量状態

地球の周りを回転している人工衛星のように、重力の作用だけで運動している物体に固定した系では、重力はつねにゼロになっている。この状態が無重量状態（無重力状態）といわれる。これは、重力と慣性力とが互いに完全に打ち消し合うためである。人工衛星の場合は、回転による遠心力という慣性力と重力とが互いに打ち消し合っている。また、自由落下する箱の系でも無重量になるが、この場合は落下の加速度運動による慣性力が重力と打ち消し合っている。宇宙ステーションのなかでは地上重力の100万分の1程度の無重力状態が実現できる。この微小重力のもとで、燃焼や表面張力による流体運動の実験、製薬や材料の開発、生物の成長や生理への影響の研究がなされる。

［佐藤文隆］

地球と重力

地上における重力の大きさは地球の全質量によって決まっている。これによって引き起こされる加速度は、9.80m/s²で、重力加速度とよばれ、gで表される。gの値は、地球の回転、形が完全に球形でないこと、組成が完全に一様でないこと、などの理由で一定でなく、場所によって、わずかに異なる。

　地球の内部、山や海、大気などの現象は、すべて重力が支配的な役割を果たしている。たとえば、プレートテクトニクスや台風なども重力の影響下にある流体や気体が熱せられたときにおこる対流に起因し、また山の高さなども重力と物体の固さとの相互関係で決まっている。大気組成に水素が少ないのは地球の重力が小さかったからである。木星では水素もとらえるほどに重力が強いが、月では大気をとらえることができないほどに重力が小さい。

　地上の生物の構造や生理的機能も重力の大きさと密接に関係している。たとえば生物の姿勢を規定する要因の一つに重力がある。無重力の世界に浮遊している生物があるとすれば、その生物は重力の方向に対する傾斜も特別の形態も必要としないが、重力の世界に住む生物はまず重力に対する体軸の位置を決めなければならない。つまり生物の姿勢は重力に影響されるのである。重力環境にある人間が、宇宙飛行などで重力条件が変化した場合の生体への影響は未知の問題である。

［佐藤文隆］

『山内恭彦・内山竜雄・中野董夫著『一般相対性および重力の理論』（1967・裳華房）』▽『ペーター・G・ベルグマン著、谷川安孝訳『重力の謎――一般相対性理論入門』（1969・講談社）』▽『M・ワシリエフ、K・スタニュコヴィチ著、金光不二夫訳編『重力と相対性理論』（1970・東京図書）』▽『ジャヤント・V・ナーリカー著、中村孔一訳『重力――宇宙を支配する力の謎』（1986・日経サイエンス社、日本経済新聞社発売）』▽『藤井保憲著『超重力理論入門』（1987・マグロウヒルブック）』▽『藤井保憲著『「統一理論」――自然界の4つの力は統一できるか？』（1993・学習研究社）』▽『菅野礼司著『力とは何か』（1995・丸善）』▽『ハラルド・フリッチ著、桜山義夫訳『アインシュタイン vs ニュートン――曲がった時空をめぐって』（1999・丸善）』▽『ハットフィールド編、リチャード・フィリップス・ファインマンほか著、和田純夫訳『ファインマン講義　重力の理論』（1999・岩波書店）』▽『二間瀬敏史著『図解雑学　重力と一般相対性理論』（1999・ナツメ社）』▽『藤本博巳・友田好文著『重力からみる地球』（2000・東京大学出版会）』▽『山本義隆著『磁力と重力の発見3　近代の始まり』（2003・みすず書房）』

[参照項目] | アインシュタイン | 一般相対性理論 | エネルギー | 遠隔作用 | 加速度 | 慣性 | 近接作用 | 原子核 | 国際宇宙ステーション | 質量 | 重力場 | 相互作用 | 相対性理論 | 素粒子 | 素粒子論 | 力 | 電磁場 | 統一場理論 | ニュートン | 万有引力 | 落下運動

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

重力 (じゅうりょく)
gravity

重力という語は宇宙論などでは万有引力のことをさすこともあるが，地球についていう場合には地球上の物体にはたらく地球の万有引力と地球自転による遠心力との合力をさす（図1）。われわれにはこの重力は物体の重量として感じられる。人工衛星のように地球の自転とは無関係な物体の運動を論ずる場合には遠心力の成分は除いて取り扱う。

　地球上で1kgの物体に作用する重力の強さは約9.8Nでほとんど一定である。したがって重力は物理学における力の基準として重要である。しかし，くわしくみると重力は場所により，また時間により変化する。重力の大きさを表すには習慣的に重力によって生ずる自由落下速度を使う。1cm/s²の大きさの加速度を1Gal（ガル）という。単位名はガリレオ・ガリレイにちなむ。地表における重力の大きさは約980Galである。1Galの10⁻³を1mGal，10⁻⁶を1μGalということは他の単位と同様である。ただし，この単位はSI（国際単位系）としては暫定的に使用が認められているだけのもので，将来はSI組立単位のm/s²の単位に移行すべきものである。重力の方向すなわち振子の支点からおもりを結ぶ方向が地球上で〈下〉であり，これと垂直な方向が水平方向であることはいうまでもなく，重力は上下水平という方向の基準としても重要な役割を負っている。

重力値

地球上の場所により重力の大きさ（重力値）が異なるのは，（1）測定点の標高が場所ごとに異なること，（2）周囲の地形の影響が場所により等しくはないこと，（3）地球が球体でなく回転楕円体状であること，（4）自転による遠心力が緯度により異なること，（5）地球の内部構造が一様でないこと，といったような諸原因による。これらが重なって作用するため，重力値は細かくみると地球上で複雑な分布を示す。

　地表付近で高度の増加に応ずる重力値の減少は0.3086mGal/mの程度であるが，場所により1割程度の変動がある。

　周囲の地形の影響は，たとえば険しい山岳のふもとでは山体が上向きの引力を及ぼしている（万有引力）であろうから，地球本来の引力はその分だけ減殺されているはずであるというような効果のことである。このような地形の影響は山岳地帯で数十mGalに達するとともに測定点ごとに異なるので，たとえば地下構造を調査する際に多数の測定点の重力値を共通基準面における値にひき直すためには，高度の異なりによる影響とともに取り除かなくてはならない。

　地球が球形でないこと，また遠心力が緯度により異なることによる重力の差異は直接地球の形状の反映であるから，地球の形状を研究する測地学にとって重要なデータである。重力の成分のうち自転遠心力による分は，最大となる赤道でも3.39Galで，重力自身の大きさの0.35%程度である。一方，現実には赤道と南北両極とで重力値は5.19Galの差がある。このように赤道と両極間の重力差が3.39Galより大きく5.19Galであるということは，地球がくわしくみると球とは多少異なる形をしていることをうかがわせる。現実に地球が南北に扁平な回転楕円体とみなせることはよく知られているとおりである。地球をそのような回転楕円体とみなすと，その表面における重力値は緯度の関数として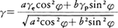，と表される。これをソメリアナSomiglianaの式という。式の各量は，φが緯度，aとbは地球の赤道と極の半径，γ_eとγ_Pは赤道と極における重力値である。ふつうこの式は

　γ＝γ_e（1＋βsin²φ＋β′sin²2φ）

の形に簡略化して使われることが多い。式中の係数は地球の質量や扁平率等の諸元と以下のような関係があることがわかっており，これから重力の分布と地球の一般的な形状との関連がつけられるので，この式は測地学にとって重要である。具体的には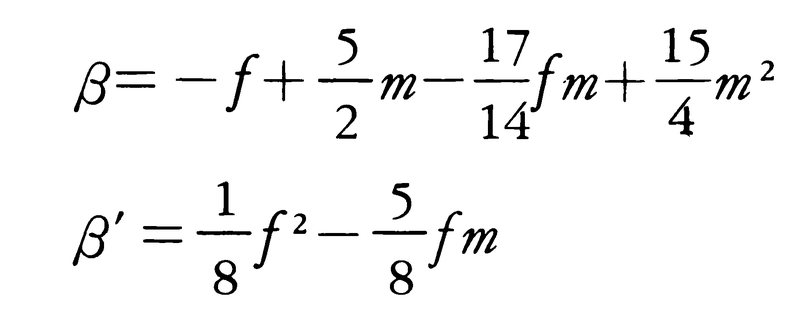

と表せる。ここにfは地球の扁平率（＝（a－b）/a），m＝ω²a²b/（GM），ωは地球自転角速度，Gは万有引力定数，Mは地球の質量である。βの式は直接に赤道・極間の重力差と地球の幾何学的な形状を表す扁平率とを結びつける式として重要である。この式で表される関係をクレーローClairaultの定理という。この定理で注目されるのは，重力扁平率βと幾何学的扁平率fの和はほぼ5/2mに等しく一定であるということである。このことから，地球の形が球に近くfが小さいほど，βは大きくなる，すなわち赤道・両極間の重力差は（小さくなるのではなく）かえって大きくなくてはならないという有名なクレーローの逆説が帰結されるのである。

正規重力

上式で表されたγは地表の重力の平均的な分布を与えるものとして正規重力と呼ばれる。1979年キャンベラで開かれた国際測地学地球物理学連合は測地基準系1980を採択した。その中に

　γ＝9.7803267715（1＋0.0052790414sin²φ＋0.0000232718sin⁴φ＋0.0000001262sin⁶φ＋0.0000000007sin⁸φ）　（m/s²）

　（誤差～10⁻⁴mGal）　

およびその簡略形

　γ＝9.780327（1＋0.0053024sin²φ－0.0000058sin²2φ）　（m/s²）　（誤差～0.1mGal）　

が正規重力式として含まれている。今後はこれらの式が正規重力を表す式として正式に使用されるべきである。従来，1930年国際式の名のもとに下の式が使用されてきた。

　γ＝978.049（1＋0.0052884sin²φ－0.0000059sin²2φ）　（Gal）　

これらの式で表される重力値はしばしば標準重力とも呼ばれてきたが，現在では正規重力と呼ぶように推奨されている。

　ところで，新旧の正規重力値を比較すると，新しい式の方が従来の式に比べ全体的に重力値が小さく表示されている。この原因は1930年式の基準となったポツダムの重力測定に誤差が含まれていたためである。新しい1980年式では人工衛星の軌道解析から得られた資料が使われていて，一応地上の重力測定とは無関係になっている。ただし，人工衛星は高空を航行するので，固体地球部分や海洋の引力とともに大気の引力の影響も受けている。そのような人工衛星の運動から得られた正規重力は大気の引力も含んだものとなっている。そのため地上の重力測定と正規重力とを比較する際には，測定重力値に0.87－0.0965h（mGal）（hの単位はkm）を加えて比較するように勧告が出されている。

重力基準網

正規重力式がa，f，ω，G，Mなどで決定される回転楕円体地球に対する理論的な式であるのに対し，より詳細な重力の分布を知るために世界各地で重力値が実測されている。この測定値をとりまとめて国際重力基準網1971（IGSN71，International Gravity Standardization Network 1971）という新たな重力網が完成している。それまで世界各地の重力値は1906年発表のポツダムで行われた可逆振子による絶対測定を唯一の基準にして決定され，ポツダム系重力値と呼ばれてきた。その後アメリカ，イギリス，ソ連等で実施された絶対測定と比較した結果，ポツダムの測定結果は約14mGal過大であることがわかった。ポツダムの結果に準拠して得られた各地の重力値はすべてこの過大分を含んで求められていることになる。新しいIGSN71の制定にあたっては，絶対測定10種，重力振子の1200回の測定，重力計による1万2000個の測定が使用された。これらのデータを使って世界の主要地点1854点の重力値が決定あるいは再決定された。おおまかにいって，古いポツダム系に比べ新しいIGSN71系の重力値は約14mGal小さく求められている。したがってここ当分の間，重力値にはポツダム系とIGSN71系の2種類の重力値が混用される状態がつづくので，注意が必要である。

　日本国内についてはIGSN71に基づいて日本重力基準網（JGSN75）が1975年に国土地理院によって制定された。JGSN75には122点の測定点が含まれ，0.1mGalの精度で重力値が与えられている。JGSN75に含まれる重力点のうち，重力値が最大なのは稚内の980622.73mGalであり，最小は石垣島の979006.06mGalである。

重力異常と地殻構造

重力実測値を正規重力値と比較して各地点の重力値が過大であるか過小であるかを知ることができる。この過大（小）量を重力異常という。図2重力異常のうちブーゲー異常といわれるものは地下構造に関係をもち，地下に過剰質量があればそこでは異常が正，不足なら負という特性をもつ。本州太平洋岸沖には帯状の負の異常があり，これは太平洋プレートの沈みこみに関連した質量不足である。また本州中央部山岳地帯に対応する負の異常は，山岳の過剰質量を地下で補償しているいわゆるアイソスタシーによる質量欠損に由来すると解釈することができる。東北日本は西南日本に比べ正の異常が目立つが，このことは地殻が薄く密度の大きいマントルがせり上がっていることを示唆する。そして東北日本で地殻が薄いということは，地震波の伝搬状況からも推定されている。種々の物理学的な測定の中でも重力測定は最高の精度と信頼度をもったものであるから，地震観測のような地球物理学的手段で推定される地下構造は重力測定の結果と矛盾するものであってはならない。
執筆者：村田 一郎

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

重力【じゅうりょく】

地球上の物体に働く地球の引力（万有引力）と地球の自転による遠心力の合力。後者はそれが最大の値をとる赤道上において引力の約290分の１に当たる。重力の大きさは単位質量に働く力，つまり重力加速度（単位m/s²またはガル）で表され，通常1000分の１のミリガルで測定される。1979年国際測地学地球物理学連合は，地表の重力の平均的な分布を与える正規重力（従来は標準重力という）の公式を，これまでの1930年公式を廃し，新たに1980年公式を採択した。新公式の簡略形では，緯度Φの地点の海面上での重力γ＝9.780327（１＋0.0053024sin²Φ−0.0000058sin²２Φ）（m/s²）で与えられる。地球上の地点によって重力値が異なるのは，測定点の標高が場所ごとに異なること，周囲の地形の影響が場所ごとに等しくないこと，地球が球でなく回転楕円体状であること，自転による遠心力が緯度により異なること，地球の内部構造が一様でないことなどが原因である。したがって重力の測定（重力計）は地球物理学上，重要なテーマで，世界各地で重力値が実測され国際重力基準網1971（IGSN71）がつくられた。日本ではIGSN71に基づいて国土地理院が日本重力基準網1975（JGSN75）を制定，122点の重力値が測定されている。最大は稚内の98万622.73ミリガル，最小は石垣島の97万9006.06ミリガルである。なお，重力ということばは地球に限らず，宇宙論などでは万有引力の意味で使われる。
→関連項目鉛直線｜重量（物理）｜重力異常

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

重力
じゅうりょく
gravity

地球上の物体に作用する地球の万有引力。物体に働く重力の強さをその物体の重量または重さという。重力によって物体が得る加速度は同一地点ではすべての物体に対し同じであって，これを重力加速度という。重力加速度はほぼ 9.80m/s² であるが，高さや緯度によって少し異なる。高地になるほど重力加速度が小さいのは，地球の中心からの距離が増大して万有引力が小さくなるためである。平均海面での値に高度補正した重力を標準重力という。地球は自転するので，実測される重力は万有引力と自転に基づく遠心力との合力であって，これを見かけの重力ということもある。見かけの重力は緯度が小さくなるほど減少するが，これは低緯度ほど外向きの遠心力が大きいのと，地球が球ではなく赤道のほうにふくらんだ回転楕円体のためである。なお，物体間の万有引力を単に重力 gravitationということがある。

出典　ブリタニカ国際大百科事典 小項目事典

パラグライダー用語辞典

重力

空を飛ぶパラグライダーには、一見、重力は邪魔な存在かのように見える。しかし実はこの重力が働くからこそ、自由に滑空する事が可能となっている。

出典　

世界大百科事典（旧版）内の重力の言及

【相対性理論】より

…　特殊相対性理論が特殊と呼ばれるのは，考慮する座標変換が慣性系どうしの間のものに限られているからであるが，もっと一般的な座標変換まで取り扱う理論は15年になって発表され，一般相対性理論と名付けられた。これは，特殊相対性理論よりもさらに革新的な内容を含む重力の理論となるのであるが，この間の事情を理解する手始めとして，ニュートンの力学における慣性系に関して説明しておかなければならない。
【慣性系】
　慣性系とは，ニュートンの運動法則が成り立つ座標系のことである。…

【万有引力】より

…これを万有引力の法則といい，G＝6.6720×10^－11N･m²･kg^－2は万有引力定数と呼ばれる定数である。Gがこのように小さいため，地上の物体相互間の万有引力は感知できないほど弱く，地球と地上の物体との間の万有引力をわれわれは重力(の主要部分)として感じている。万有引力は天体間の力の主役として，天文学ではきわめて重要である。…

※「重力」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」