フーリエ変換（読み）フーリエヘンカン（英語表記）Fourier transformation

デジタル大辞泉

フーリエ‐へんかん〔‐ヘンクワン〕【フーリエ変換】

主に、与えられた関数を別の周期関数に分解して表現する際に用いられる変換。ある信号に含まれる周波数成分の解析など、通信・画像処理などさまざまな分野で広く利用される。FT（Fourier transformation）。
[補説]ある関数f（x）に対し、f（x）とe^－2πixtの積を、xについて区間［－∞, ∞］で積分して関数F（t）が得られるとき、f（x）からF（t）への変換をフーリエ変換とよぶ。f（x）が特定の条件を満たす場合、その逆変換が存在し、F（t）からf（x）が得られ、逆フーリエ変換またはフーリエ逆変換とよぶ。

出典　小学館

日本大百科全書(ニッポニカ)

フーリエ変換
ふーりえへんかん
Fourier transformation

実軸上の関数f(x)に対し、そのフーリエ変換を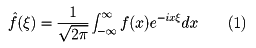

で定義する。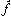(ξ)が適当な条件を満たせば、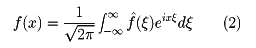

が成り立つ。これをフーリエの反転公式という。

　f(x)が偶関数のとき、（1）、（2）はそれぞれ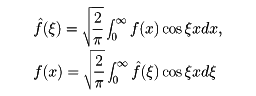

また奇関数のときは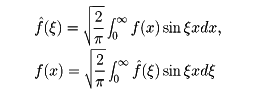

となる。

　f(x)∈L¹(-∞,∞)ならば、そのフーリエ変換（1）が定義され、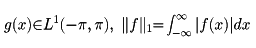

とすると、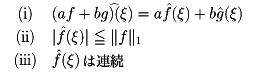

　さらに、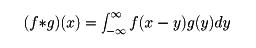

と定義すれば、(f*g)(x)∈L¹(-∞,∞)となり、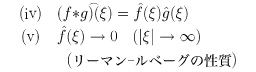

などが成り立つ。

　たとえば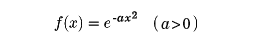

とすると、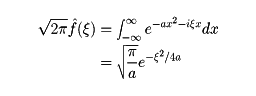

とくに、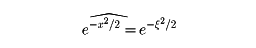

となり、フーリエ変換で変わらない。

　この例の関数は急減少関数、すなわち、無限回連続微分可能で、任意の自然数k、lに対し、
　　x^lf^(k)(x)→0　(|x|→+∞)
となっている。そのような関数の全体を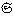で表すと、f∈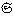⇒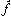∈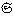となり、反転公式が成り立つ。よって、フーリエ変換を超関数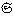′で定義する方法がある。

　フーリエ変換の他の一般への拡張は、f∈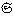ならば、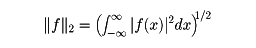

とすると、
　　‖f‖₂=‖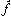‖₂　（3）
　となるから、任意のL²(-∞,∞)の関数にフーリエ変換が定義され、（3）が成り立つ。これをプランシュレルの定理という。これから、フーリエ変換はL²(-∞,∞)上の等長変換であることがわかる。

［洲之内治男］

多変数のフーリエ変換

フーリエ級数やフーリエ変換は多変数の関数f(x₁,x₂,……,x_n)に拡張される。それには、x=(x₁,x₂,……,x_n),ξ=(ξ₁,ξ₂,……,ξ_n)に対し、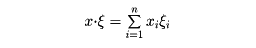

とし、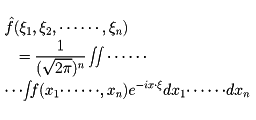

によって定義すればよい。多くの結果は一変数のときと同様に成り立ち、偏微分方程式などに応用される。

［洲之内治男］

[参照項目] | 超関数

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

フーリエ変換
フーリエへんかん
Fourier transformation

(－∞，∞) で定義された実数値をとる1つの関数 f(x) が与えられたとき，フーリエ積分
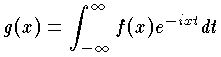を考えて，関数 f(x) に関数 g(x) を対応させる変換を，フーリエ変換という。また，g(x) を f(x) のフーリエ変換という。フーリエ級数もこれと同じ形で，関数 f(x) に数列 {c_n} を対応させている。それで，フーリエ積分とフーリエ変換を総称してフーリエ変換ということもある。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のフーリエ変換の言及

【音声情報処理】より

…また，同時にピッチ抽出も行う。スペクトル分析は，通常フーリエ変換か線形予測分析により行われ，ピッチ抽出は自己相関分析により行われることが多い。
[音声合成]
　調音器官を円筒形の縦続接続で近似し，電気回路のシミュレーションで音声を生成したり，スペクトル包絡を特徴づける少数の強い周波数成分(低い方から第1フォルマント，第2フォルマント……という)から音声を生成する方法(声道アナログ方式，ターミナルアナログ方式)が研究されてきたが，このような近似的な生成法では，鼻にかかったような機械的な音になってしまう。…

【高速フーリエ変換】より

…これを拡張して，任意の関数s(t)も，ある条件のもとで次のような周波数成分S(f)に分解できることが知られている。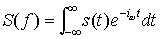S(f)をs(t)のフーリエ変換という。s(t)が，離散的なt₀,t₁,t₂，……，t_Nに対してのみ定義されているときは，S(f)の代りに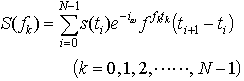，が用いられる。…

【フーリエ解析】より

…フーリエ級数，フーリエ変換などを用いて関数の性質を研究し，種々の応用を論ずる分野をフーリエ解析という。実験によって数値的に与えられた関数のフーリエ級数を求める方法は調和解析といわれる。…

【フーリエ積分】より

…(－∞，∞)において積分可能な関数f(x)に対して，次の関数F(t)を考える。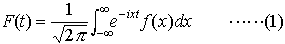この右辺の積分をフーリエ積分といい，左辺の関数F(t)をf(x)のフーリエ変換という。また(1)によるfからFへの変換をもフーリエ変換という。…

※「フーリエ変換」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」