精選版 日本国語大辞典 「ユークリッド空間」の意味・読み・例文・類語
ユークリッド‐くうかん【ユークリッド空間】
改訂新版 世界大百科事典 「ユークリッド空間」の意味・わかりやすい解説
ユークリッド空間 (ユークリッドくうかん)
Euclidean space
n個の実数を並べた組(x1,x2,……,xn)全体の集合をRnで表すとき,座標法により,直線,平面,空間の点はそれぞれR1,R2,R3の要素と1対1に対応する。そして,座標がx,yである直線上の2点間の距離は,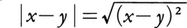 で与えられ,直交座標を用いれば,座標が(x1,x2),(y1,y2)である平面上の2点間の距離は,
で与えられ,直交座標を用いれば,座標が(x1,x2),(y1,y2)である平面上の2点間の距離は,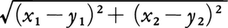 で,座標が(x1,x2,x3),(y1,y2,y3)である空間の2点間の距離は,
で,座標が(x1,x2,x3),(y1,y2,y3)である空間の2点間の距離は,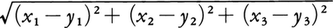 で与えられる。そこで,一般のnについてもRnの要素(x1,x2,……,xn)を点とみなして,これを一つの文字xで表し,2点x=(x1,x2,……,xn),y=(y1,y2,……,yn)に対し,
で与えられる。そこで,一般のnについてもRnの要素(x1,x2,……,xn)を点とみなして,これを一つの文字xで表し,2点x=(x1,x2,……,xn),y=(y1,y2,……,yn)に対し,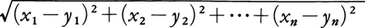 をxとyの間の距離と呼ぶことにする。このようにしたときのRnをn次元ユークリッド空間という。上でみたことにより,直線はR1,平面はR2,空間はR3と同一視される。Rnの2点x,yの間の距離を|x-y|で表すとき,Rnの3点x,y,zに対し,
をxとyの間の距離と呼ぶことにする。このようにしたときのRnをn次元ユークリッド空間という。上でみたことにより,直線はR1,平面はR2,空間はR3と同一視される。Rnの2点x,yの間の距離を|x-y|で表すとき,Rnの3点x,y,zに対し,
|x-z|≦|x-y|+|y-z|
が成り立つ。Rnの点x=(x1,……,xn),y=(y1,……,yn)と実数λ,μに対し,点(λx1+μy1,……,λxn+μyn)をλx+μyで表す。Rnのm+1個の点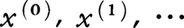
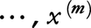 に対し,
に対し,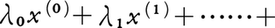
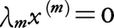 (ここにλ0,……,λmは実数で,λ0+……+λm=0)ならばλ0=λ1=……=λm=0という条件が成り立つとき,これらの点は一般に位置にあるといい,このときλ0+λ1+……+λm=1をみたすすべての実数λ0,λ1,……,λmに対する点
(ここにλ0,……,λmは実数で,λ0+……+λm=0)ならばλ0=λ1=……=λm=0という条件が成り立つとき,これらの点は一般に位置にあるといい,このときλ0+λ1+……+λm=1をみたすすべての実数λ0,λ1,……,λmに対する点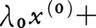
 全体の集合をRnのm次元平面という。とくにn-1次元平面を超平面,一次元平面を直線という。Rnの点aとr>0に対し,|x-a|=rをみたす点x全体の集合をaを中心としrを半径とするn-1次元球面という。RnからRnの上への1対1対応で,2点間の距離を変えないものをユークリッド空間の合同変換という。
全体の集合をRnのm次元平面という。とくにn-1次元平面を超平面,一次元平面を直線という。Rnの点aとr>0に対し,|x-a|=rをみたす点x全体の集合をaを中心としrを半径とするn-1次元球面という。RnからRnの上への1対1対応で,2点間の距離を変えないものをユークリッド空間の合同変換という。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「ユークリッド空間」の意味・わかりやすい解説
ユークリッド空間
ユークリッドくうかん
Euclidean space
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内のユークリッド空間の言及
【距離空間】より
…一般に,n個の実数の組(x1,x2,……,xn)全体の集合において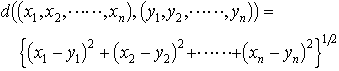 と定義すれば距離空間が得られる。これをn次元ユークリッド空間Euclidean spaceという。また閉区間[a,b]で定義された連続関数は,その2元f,gに対して,d(f,g)=max{|f(x)-g(x)|;a≦x≦b}と定義すれば距離空間となる。…
と定義すれば距離空間が得られる。これをn次元ユークリッド空間Euclidean spaceという。また閉区間[a,b]で定義された連続関数は,その2元f,gに対して,d(f,g)=max{|f(x)-g(x)|;a≦x≦b}と定義すれば距離空間となる。…
【距離空間】より
…一般に,n個の実数の組(x1,x2,……,xn)全体の集合において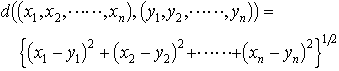 と定義すれば距離空間が得られる。これをn次元ユークリッド空間Euclidean spaceという。また閉区間[a,b]で定義された連続関数は,その2元f,gに対して,d(f,g)=max{|f(x)-g(x)|;a≦x≦b}と定義すれば距離空間となる。…
と定義すれば距離空間が得られる。これをn次元ユークリッド空間Euclidean spaceという。また閉区間[a,b]で定義された連続関数は,その2元f,gに対して,d(f,g)=max{|f(x)-g(x)|;a≦x≦b}と定義すれば距離空間となる。…
※「ユークリッド空間」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


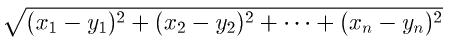 で与えられる空間のこと。
で与えられる空間のこと。