改訂新版 世界大百科事典 「位相群」の意味・わかりやすい解説
位相群 (いそうぐん)
topological group
x,yが正数のとき積xyおよび逆数x⁻1はまた正数であるから,正数全体の集合は1を単位元として群をつくる。この際,(x,y)をxyにうつす関数およびxをx⁻1にうつす関数はともに連続である。一般に,群Gが与えられたとき,G×GからGへの写像が(x,y)を積x・yにうつすことにより,またGからGへの写像がxを逆元x⁻1にうつすことにより得られるが,Gに位相が導入されているときは,これらの写像の連続性が議論できる。群Gが同時に位相空間であって,上の二つの写像がともに連続となるとき,Gを位相群という。簡単な例として,上述の正数の乗法群のほかに,実数の加法群,複素数の加法群,0以外の複素数の乗法群,平面上の1点のまわりの回転群などがある。また,二次の行列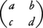 でad-bc≠0を満たすもの全体の集合は行列の積に関して群をつくるが,二つの行列が“近い”とはこれら行列の対応する各成分が“近い”ことであるとしてこの群に位相を導入すれば,それは位相群になる。位相群Gの単位元のある近傍がユークリッド空間と同相のとき,Gを局所ユークリッド群locally Euclidean groupという。上述の例はすべて局所ユークリッド群である。〈局所ユークリッド群はつねにリー群であるか〉というヒルベルトの第5問題は1900年に提案されて以来多くの研究者の関心をひいたが,52年ごろモンゴメリーDeane Montgomery(1909- )や山辺英彦(1923-60)らによって肯定的に解決された。
でad-bc≠0を満たすもの全体の集合は行列の積に関して群をつくるが,二つの行列が“近い”とはこれら行列の対応する各成分が“近い”ことであるとしてこの群に位相を導入すれば,それは位相群になる。位相群Gの単位元のある近傍がユークリッド空間と同相のとき,Gを局所ユークリッド群locally Euclidean groupという。上述の例はすべて局所ユークリッド群である。〈局所ユークリッド群はつねにリー群であるか〉というヒルベルトの第5問題は1900年に提案されて以来多くの研究者の関心をひいたが,52年ごろモンゴメリーDeane Montgomery(1909- )や山辺英彦(1923-60)らによって肯定的に解決された。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


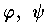 がともに
がともに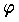 は
は