固体の熱容量（読み）コタイノネツヨウリョウ

化学辞典 第2版

固体の熱容量
コタイノネツヨウリョウ
heat capacity of solid

固体の熱容量に関しては，固体元素の原子熱容量は6.2 kcal mol^－1(26 kJ mol^－1)というデュロン-プティーの法則があり，また固体化合物については，モル熱容量は構成元素の原子熱容量の和に等しいというコップの法則がある．固体の熱容量の古典的理論では，1 mol の固体元素の N_A 個の原子を3N_A個の振動子とみなし，エネルギー均等分配の法則により，1振動子ごとにRの熱容量をもつと仮定し，

C_V ＝ 3R ≈ 6 cal deg^－1 mol^－1
を得る．これはデュロン-プティーの経験法則に支持を与えるものであるが，一般に見られる低温での原子熱容量の減少を説明できない．A. Einstein(アインシュタイン)(1907年)は量子論を導入し，

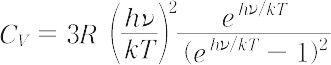
の式を導いた．νはその固体の特有振動数であり実験的に決められる．この式は低温における原子熱容量の低下を説明できるが，実験との一致は完全ではない．P.J.W. Debye(デバイ)(1912年)は3N_A個の振動子は独立ではなく，互いに結合し，3N_A個の異なる振動数が存在するものとし，その分布は均質等方的な弾性体中の音波の振動数分布に等しいと仮定し，次式を得た．

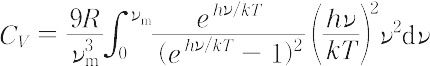
ν_m は最大振動数，hν/kは温度の次元をもち，hν_m/kはその固体の特有の温度でθで表す．積分の結果は

C_V ＝ f(T/θ)
の形となり，この関数形はすべての固体元素について同じである．実際，この関係はすべての元素について成り立ち，C_V をT/θに対して目盛ると一本の曲線上にのる．十分高い温度では C_V ＝ 3Rとなり古典理論と同じになる．極低温では

C_V ＝ aT ³ (aは定数)
となる．極低温での熱容量の測定は実験的に困難であるから，この簡単な関係式は有用である．

出典　森北出版「化学辞典（第2版）」