慣性だ円体（読み）カンセイダエンタイ（英語表記）ellipsoid of inertia

化学辞典 第2版

慣性だ円体
カンセイダエンタイ
ellipsoid of inertia

質量 m_i なる質点の集まりからなる剛体内の点Oを原点としてx，y，z軸をとると，この主軸系における慣性テンソルの成分は，

　　I_xx ＝ Σ m_i(y_i² ＋ z_i²)，I_yy ＝ Σ m_i(z_i² ＋ x_i²)

　　I_zz ＝ Σ m_i(x_i² ＋ y_i²)，I_xy ＝ Σ m_ix_iy_i

　　I_yz ＝ Σ m_iy_iz_i，I_zx ＝ Σ m_iz_ix_i

である．また，Oを通る直線OSの方向余弦を(λ，μ，ν)とすると，この直線のまわりの慣性モーメントは，

　　I ＝ I_xxλ² ＋ I_yyμ² ＋ I_zzν² － 2I_xyλμ － 2I_yz μν － 2I_zx νλ

となる．OSの方向にOから

r ＝ 1/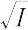
の距離にある点R(x，y，z)をとり，慣性モーメントがIであるような軌跡を求めると，

I_xxx ² ＋ I_yyy ² ＋ I_zzz ² － 2I_xyxy － 2I_yzyz － 2I_zxzx＝1

のだ円体面となる．このような面をもつだ円体を慣性だ円体という．さらに，

I_xy ＝ I_yz ＝ I_zx ＝ 0
となるような方向にとった主軸を慣性主軸とよび，この主軸系におけるx，y，z軸のまわりの慣性モーメント I_xx，I_yy，I_zz を主慣性モーメントという．分子スペクトルでは，分子の回転を解析するときに分子を慣性だ円体とみなして取り扱う．[別用語参照]回転スペクトル

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

慣性楕円体
かんせいだえんたい
ellipsoid of inertia

直角座標軸に関する剛体の慣性モーメント，慣性乗積を係数とする次の二次曲面は楕円体面となる。

I_xxx²＋I_yyy²＋I_zzz²＋2I_xyxy＋2I_yzyz＋2I_zxzx＝1

これを慣性楕円体という。原点を通る直線に関する慣性モーメントは，原点からこの直線と楕円体面の交点までの距離の2乗の逆数に等しい。慣性楕円体はその剛体に固有で固着していると考えられるので，剛体の回転は慣性楕円体の回転の様子によって表現できる。これをポアンソの表現という。慣性楕円体の主軸を慣性主軸といい，剛体の回転に関する運動方程式を慣性主軸方向の成分に分解したものがオイラーの運動方程式である。

出典　ブリタニカ国際大百科事典 小項目事典