精選版 日本国語大辞典 「剛体」の意味・読み・例文・類語
ごう‐たいガウ‥【剛体】
改訂新版 世界大百科事典 「剛体」の意味・わかりやすい解説
剛体 (ごうたい)
rigid body
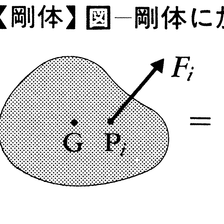
力を加えても変形しない理想的な物体。生卵などは回転すると形はほとんど変わらないが,内部で流動を生ずるから剛体に近いとはいえない。したがって,物体内のどの2点をとってもその距離が不変であるものを剛体といったほうが正確である。固体の運動を扱うとき,変形や振動を考えると非常にめんどうになるが,剛体という理想化を行うと,運動が6個の変数で記述できるので,扱いがずっと簡単になる。変数のとり方にはいろいろあるが,剛体の任意の1点(例えば重心)の位置X,Y,Zと,剛体に固定した直交座標系の方位を示すオイラー角(回転運動)θ,φ,ψとを用いることができる。X,Y,Zは並進運動,θ,φ,ψは回転を表す。剛体の1点Piに加えられた力Fiの働きは,重心Gに互いに打ち消し合う力Fiと-Fiをつけ加えてみればわかるように,Gに加えられた力Fiと,モーメントが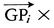
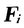 の偶力とに分けられる(図参照)。前者はR(X,Y,Z)で表される重心の運動を,
の偶力とに分けられる(図参照)。前者はR(X,Y,Z)で表される重心の運動を,
によって決め,後者はオイラーの方程式によって回転運動を決める。
執筆者:小出 昭一郎
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「剛体」の意味・わかりやすい解説
剛体【ごうたい】
→関連項目運動の法則|気体分子運動論|偶力|こま(独楽)|コワレフスカヤ|作用点|実体振子|連続体(物理)
出典 株式会社平凡社百科事典マイペディアについて 情報
日本大百科全書(ニッポニカ) 「剛体」の意味・わかりやすい解説
剛体
ごうたい
力が働いても変形することのない物体をいう。しかし剛体というのは物質の種類に直接関係しない。多くの固体は、その空間的な運動あるいはつり合いなどを研究するときは剛体として扱われるが、その変形を考察するときは剛体ではない。人体のようなものも、肢体を動かさない運動の研究に関しては剛体として扱われる場合がある。
剛体の運動は、その重心の運動と、重心の周りの回転運動とが合成されたものである。剛体のつり合いは次のように考えられる。剛体の1点に働く力がつり合うのは質点の場合と同様であるが、そのほかに、剛体は伸び縮みしないため、剛体の中の一つの線分の両端に、それと平行で互いに反対向きの大きさの等しい力を加えても、なんの影響もない。これを利用すれば、(1)力をその線上の他の点に移すことができる。(2)剛体の異なった2点に働く平行な力を一つの力に合成することができる。
このようにしても一つの力に合成できないのは、大きさが等しく平行で反対向きの二つの力であり、これを偶力という。偶力を一つの線分の両端に働くそれと垂直な二つの力で表したとき、線分の長さと力の大きさの積すなわち偶力のモーメントで特徴づけられる。結局、剛体のつり合いは、力とそのモーメントのつり合いで決めることができる。
こうしてみると、剛体とは、物体が運動やつり合いにおいてもつ性質の一側面を抽象したものであるということができる。さらに抽象化されたものが質点である。
[宮原将平]
ブリタニカ国際大百科事典 小項目事典 「剛体」の意味・わかりやすい解説
剛体
ごうたい
rigid body
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...