精選版 日本国語大辞典 「二次曲面」の意味・読み・例文・類語
にじ‐きょくめん【二次曲面】
ブリタニカ国際大百科事典 小項目事典 「二次曲面」の意味・わかりやすい解説
二次曲面
にじきょくめん
quadrics
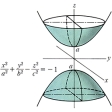
| (1) 楕円面 | x2/a2+y2/b2+z2/c2=1 | |
| (2) 二葉双曲面 | x2/a2-y2/b2-z2/c2=1 | |
| (3) 一葉双曲面 | x2/a2+y2/b2-z2/c2=1 | |
| (4) 楕円錐 | x2/a2+y2/b2-z2/c2=0 | |
| (5) 楕円放物面 | x2/a2+y2/b2-2z=0 | |
| (6) 双曲放物面 | x2/a2-y2/b2-2z=0 | |
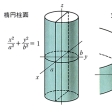
| (7) 楕円柱 | x2/a2+y2/b2-1=0 | |
| (8) 双曲柱 | x2/a2-y2/b2-1=0 | |
| (9) 放物柱 | x2-2py=0 |
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
日本大百科全書(ニッポニカ) 「二次曲面」の意味・わかりやすい解説
二次曲面
にじきょくめん
空間の直交座標x、y、zの間の二次方程式
ax2+by2+cz2+2fyz+2gzx+2hxy
+2lx+2my+2nz+d=0
で表される曲面を二次曲面という。座標系を適当に平行移動したり回転移動したりすれば、二次曲面は以下の七つの標準形のいずれかになる(ただし、以下のa、b、cは原式のものとは異なる)。
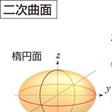
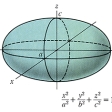
(1)楕円面(だえんめん)
(x2/a2)+(y2/b2)+(z2/c2)=1
どの平面で切っても切り口は楕円である。また、この二次曲面だけは有限の範囲に収まっている。a=bのとき、ラグビーボールまたは円盤に似た形で、z軸の周りの回転面となる。これを回転楕円面という。a=b=cのときは半径aの球面となる。
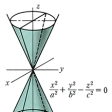
(2)二次錐面(すいめん)
(x2/a2)+(y2/b2)-(z2/c2)=0
z軸に垂直に切ると切り口はすべて楕円である。原点を通る平面で切ると切り口はすべて2本の直線となるから、線織面(せんしきめん)である。ここで線織面とは、ある直線群が織り成す曲面をいう。
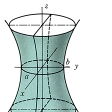
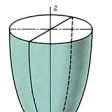
(3)一葉双曲面
(x2/a2)+(y2/b2)-(z2/c2)=1
z軸に垂直に切ると切り口は楕円で、z軸を含む平面で切ると切り口は双曲線である。原点から遠ざかるにつれて(2)に限りなく近づいていくので、(2)をこの曲面の漸近面(ぜんきんめん)という。またこの曲面は線織面である。a=bのとき、くびれたところの近くは鼓(つづみ)に似た形で、z軸の周りの回転面となる。これを回転一葉双曲面という。
(4)二葉双曲面
(x2/a2)+(y2/b2)-(z2/c2)=-1
z軸に垂直に切ると切り口は楕円で、z軸を含む平面で切ると切り口は双曲線である。この曲面も原点から遠ざかるにつれて(2)に限りなく近づくので、やはり(2)が漸近面となる。
(5)楕円放物面
(x2/a2)+(y2/b2)=2z
z軸に垂直に切ると切り口は楕円で、z軸を含む平面で切ると切り口は放物線である。a=bのとき、z軸の周りの回転面で、回転放物面という。
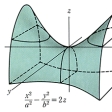
(6)双曲放物面
(x2/a2)-(y2/b2)=2z
原点の近くは馬の鞍(くら)とか峠に似た形で、線織面である。z軸に垂直に切ると切り口は双曲線または直線で、z軸に平行に切ると切り口は放物線または直線である。
(7)柱面 xy平面のある二次曲線を通りxy平面に垂直な直線群が織り成す曲面である。円柱(x2/a2)+(y2/a2)=1と、楕円柱面(x2/a2)+(y2/b2)=1と、双曲柱面(x2/a2)+(y2/b2)=1と、放物柱面(x2/a2)=2yの四種類であるが、このうち円柱だけが回転面である。
[高木亮一]
改訂新版 世界大百科事典 「二次曲面」の意味・わかりやすい解説
二次曲面 (にじきょくめん)
quadric
quadratic surface
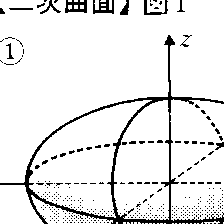
空間の直交座標(x,y,z)を用いて,実数係数の二次方程式Ax2+By2+Cz2+2Fyz+2Gzx+2Hxy+2F′x+2G′y+2H′z+D=0で表される曲面を総称して二次曲面という。係数A,B,……,H′のとりようによっては,方程式を満たす点はまったくなかったり,方程式は1点,1直線,1平面,または2平面を表すこともあるが,これらを除けば二次曲面は,適当な直交座標系を用いれば,次の形の方程式のいずれか一つで表され,かっこ内に書いた名称で呼ばれる。
このうち(1)~(5)の曲面を固有二次曲面という(図1)。二次曲面がある点に関して対称なとき,この点を二次曲面の中心といい,中心がただ一つ存在する二次曲面を有心二次曲面という。(1)~(9)のうち,(1)~(3)と(9)が有心二次曲面である。(1),(3),(4)の曲面は直線を一つも含んでいないが,(2)と(5)~(9)の曲面は無限に多くの直線によって描かれる線織面である。これらの直線をそれぞれの曲面の母線という。とくに(2)と(5)の曲面上にはそれらを描く2組の直線族があって,同じ族の2直線は交わらず,異なった族の2直線は交わっている(図2)。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「二次曲面」の意味・わかりやすい解説
出典 株式会社平凡社百科事典マイペディアについて 情報
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...