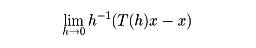発展方程式（読み）はってんほうていしき（英語表記）equation of evolution

改訂新版　世界大百科事典

発展方程式 (はってんほうていしき)
equation of evolution

時間とともに状態が変化していく物理現象があって，その変化のしかたが過去の履歴には無関係に，その瞬間の状態によって定まるならば，その変化のしかたは一つの微分方程式で記述される。このように状態の時間的発展を記述する方程式を，一般に発展方程式という。例えば熱伝導の現象において，時刻tにおける温度分布u＝u（t，x）（xは空間の点）の変化のしかたは，偏微分方程式，

　∂u/∂t＝Δu　（Δはラプラシアン）　……（1）　

で記述されるが，各時刻tに対してxの関数u（t，・）をある適当な関数空間の要素と考えて，たんにu（t）と書き，対応u→Δuをその関数空間から同じ関数空間への写像と考えて一般にAと書くと，（1）は，

　du（t）/dt＝Au（t）　……（2）　

と書くこともできる。ここでd/dtは関数空間の中での収束を使って定義された微分演算である。発展方程式は通常一つの関数空間を定めて（2）の形に記述して取り扱われる。波動方程式∂²u/∂t²＝Δuは，行列の形を使って，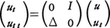

　　（u_t＝∂u/∂t，Iは恒等作用素）　

と書けるから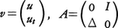，とおくとdv/dt＝Avと表され，（2）と同じ形の発展方程式になる。また，量子力学に現れるシュレーディンガー方程式は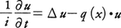，の形であるが，これは適当なヒルベルト空間において作用素H＝Δ－q（x）・を適当に定義することにより，

　du/dt＝iHu

と書けるので，これも発展方程式である。

　一般に，あるバナッハ空間Eで方程式（2）を考えるとき，uの初期値u（0）∈Eに時刻t＞0におけるuの値u（t）を対応させる作用素をT_tと書くと，任意のt，s＞0に対し，

　T_t+su（0）＝u（t＋s）＝T_tu（s）＝T_tT_su（0）

となるから，

　T_t+s＝T_tT_s　……（3）　

なる関係がある。（3）を満たす線形作用素の族｛T_t｝_t0を1パラメーター半群，または単に半群と呼ぶ。このとき（2）はh↓0のとき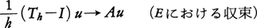，となることを意味するので，Aを半群｛T_t｝の生成作用素という。発展方程式（2）を解くことは，バナッハ空間Eにおいて，半群｛T_t｝からその生成作用素Aを特徴づけ，逆にAから｛T_t｝を構成することに帰着される。その理論は吉田耕作とヒレE.Hilleにより同時（1948）に互いに独立に確立されたので，吉田=ヒレの理論と呼ばれ，現代の解析学においてもっとも重要な理論の一つである。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

発展方程式
はってんほうていしき

A(t)を数tをパラメーターとする線形位相空間Xにおける作用素の族とするとき、u(t)を未知なX値関数とする微分方程式
　　u′(t)=A(t)u(t)　 （1）
を発展方程式という。Xをバナッハ空間とする。X上の有界線形作用素の族｛T(t):t≧0｝は次の条件（a）～（c）を満たすとき、X上の(C₀)級縮小半群とよばれる。（a）T(0)はX上の恒等作用素で、各t、sに対しT(t)T(s)=T(t+s)が成り立つ。（b）各x∈Xに対しT(t)xはtのX値関数としてt≧0で連続である。（c）各T(t)の作用素ノルムは1を超えない。｛T(t) :t≧0｝をX上の(C₀)級縮小半群とする。極限

が存在するようなxに対しこの極限をAxと置いて定まるXの線形作用素Aをこの半群の生成作用素という。生成作用素Aの定義域D(A)はXで稠密(ちゅうみつ)で、x∈D(A)のときu(t)=T(t)xは（1）をA(t)=Aとして満たすただ一つの連続的微分可能なX値関数になる。Xの線形作用素AがX上のある(C₀)級縮小半群の生成作用素であるための必要十分条件は、その定義域がXで稠密で、各λ＞0に対しそのレゾルベント(λI-A)^-1がXの有界作用素として定まり、かつその作用素ノルムがλ^-1を超えないことである（ヒレ‐吉田の定理）。この定理を基礎にしてA(t)が真にtに依存する場合、Xがもっと一般の線形位相空間の場合、作用素A(t)がかならずしも線形とは限らない場合の発展方程式の解の存在、性質が調べられている。

［小林良和］

出典　小学館　日本大百科全書(ニッポニカ)