バナッハ空間（読み）バナッハくうかん（その他表記）Banach space

改訂新版　世界大百科事典

バナッハ空間 (バナッハくうかん)
Banach space

解析学における基本的な問題を無限次元の関数空間における写像の問題として，位相的・代数的方法によって取り扱うためにS.バナッハによって導入された空間。実数の閉区間［0，1］の上で定義された複素数値連続関数の全体をXとすると，Xはふつうの関数の加法と定数（複素数）を掛ける演算でベクトル空間になっている。x₀（t）≡0なる関数が0ベクトルであって，それを単に0で表す。関数x∈Xに対して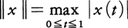，とおくと，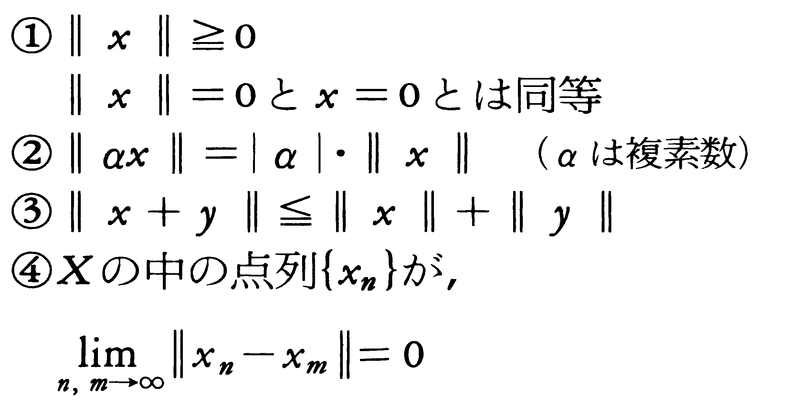

を満たすならば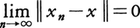，となるようなx∈Xが存在する。

　一般に，複素数体上のベクトル空間Xの各点xに対して，ベクトルxの長さに相当するノルムと呼ばれる量／x／が定義されていて，上の（1）～（4）を満たすとき，Xをバナッハ空間という。dis（x，y）＝／x－y／とおくと，これは距離の性質をもつ。（4）は実数のコーシー列は収束するという性質に相当するもので，空間Xの完備性と呼ばれる。

　バナッハ空間の例を三つあげる。

（1）位相空間S上の複素数値有界連続関数の全体C（S）において，ノルムを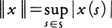，と定義する。

（2）1≦p＜∞とし実数の区間（a，b）上の複素数値可測関数x（t）で｜x（t）｜^pが積分可能なものの全体をL_p（a，b）とし，ノルムを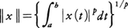，と定義する。ただし，ルベーグ測度に関してほとんどいたるところx（t）＝y（t）ならばx＝yとみなす。

（3）1≦p＜∞とし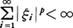，なる複素数列｛ξ_i｝の全体をl_pとし，x＝｛ξ_i｝∈l_pのノルムを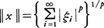，と定義する。

　これらC（S），L_p（a，b），l_pはいずれもバナッハ空間であり，本項目の最初に述べた例はC（S）のSが閉区間［0，1］の場合である。バナッハ空間の理論や，バナッハ空間を扱う現代解析学の考え方については，〈関数解析学〉の項目を参照。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

バナッハ空間
バナッハくうかん
Banach space

集合 B が次の3つの条件を満たすとき，これをバナッハ空間という。 (1) 集合 B は，実数または複素数体の上のベクトル空間である。 (2) 集合 B のおのおのの元 x に対して，そのノルム ∥x∥ が定義されている。 (3) 集合 B の2つの元 x と y に対して，x と y の間の距離を ∥x－y∥ で定義すれば，この距離に関して集合 B は完備な距離空間である。初め，関数空間としてのヒルベルト空間が論じられ，その議論がもっと一般の関数空間にも通用するように考えられた。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のバナッハ空間の言及

【数学】より

…　1920年代のヨーロッパは二つの戦争の間にあり政治的には不安定であったが，ワイマール政府の下のドイツのゲッティンゲン大学には，ヒルベルトとともにE.ネーターが活躍し，抽象代数学の研究の中心となった。同じころポーランドにはS.バナッハらがいて位相数学(トポロジー)が盛んに研究された。バナッハはヒルベルト空間の拡張であるバナッハ空間の線形作用素論を解析の諸問題に応用した。…

※「バナッハ空間」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」