確率過程（読み）カクリツカテイ（英語表記）stochastic process

デジタル大辞泉

かくりつ‐かてい〔‐クワテイ〕【確率過程】

時間の経過とともにランダムに変化する事象を、確率変数を用いて数学的に記述したもの。ブラウン運動を数学的にモデル化したウィーナー過程をはじめ、株価・為替相場、道路の交通量、都市の人口、感染症の流行など、多様な現象を表現する数理モデルとして利用される。

出典　小学館

改訂新版　世界大百科事典

確率過程 (かくりつかてい)
stochastic process

時間の経過とともに変化する偶然現象の数学的模型である。偶然量の時刻tにおける値を確率変数としてX_t（ω）（ωは根元事象）で表し，その集り｛X_t（ω）｝を確率過程という。統計学ではこれを時系列ともいう。ωを固定すると，X_t（ω）はtだけの関数になるが，これを見本関数とか標本関数などという。

　例1　硬貨を次々と投げて，表が出たら1だけ右に進み，裏なら1だけ左に進む直線上の不規則運動をランダムウォークという。t回投げたとき，X_t（ω）＝（表の出た回数）－（裏の出た回数）とおき，またX₀＝0とする。この場合ωは一連の試行に対応する。確率過程｛X_t（ω）（t＝0，1，2，……）｝は原点から出発するランダムウォークの模型である。

　例2　確率過程｛X_t（ω）（t≧0）｝があって，X₀（ω）＝0であり，t，s（t＞s）を任意にとるとき，X_t（ω）－X_s（ω）の分布がポアソン分布で，P｛X_t（ω）－X_s（ω）＝k｝＝e⁻^λ⁽^t⁻^s⁾λ^k（t－s）^k/k！（k＝0，1，2，……）となるならば，｛X_t（ω）｝をポアソン過程という。時刻0からtまでの間に起きるある種の交通事故の件数をX_t（ω）とするとき，｛X_t（ω）｝がポアソン過程とみなされる場合がある。確率過程のうち，ガウス過程，定常過程，加法過程，マルコフ過程，拡散過程，マルチンゲールなどはもっともよく研究されている。

ガウス過程

｛X_t（ω）｝を確率過程とする。任意にとったt₁，t₂，……，t_nに対して，（X_t1（ω），X_t2（ω），……，X_tn（ω））の結合分布が多次元正規分布であるとき，｛X_t（ω）｝をガウス過程という。その確率法則は，平均値m（t）＝E｛X_t（ω）｝と共分散関数ρ（t，s）＝E｛（X_t（ω）－m（t））（X_s（ω）－m（s））｝とで決まる。m（t）＝0，ρ（t，s）＝min｛t，s｝（＝tとsの小さいほう）であるガウス過程｛X_t（ω）（t≧0）｝で見本関数が連続であるものをウィーナー過程，またはブラウン運動という。これはR.ブラウンが観察した花粉の微粒子の不規則運動や，A.アインシュタインが研究した分子運動の模型を，N.ウィーナーが数学的に厳密にしたもので，ウィーナーやP.レビーの詳しい研究がある。

定常過程

確率過程｛X_t（ω）（－∞＜t＜∞）｝について，t₁，t₂，……，t_nとhとを任意にとるとき，X_t1+h（ω），X_t2+h（ω），……，X_tn+h（ω））の結合分布がhに無関係であるとき，｛X_t（ω）｝を定常過程という。これに対し，平均値m（t）が定数で，共分散関数ρ（t，s）がt－sだけの関数ρ（t－s）である確率過程を弱定常過程と呼ぶ。ρ（t）はボホナーの定理により正測度μのフーリエ変換として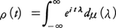，と表される（スペクトル分解）。ヒンチンA.Y.Khinchin（1894-1959）はこの分解を使って定常過程の諸性質を研究した。弱定常過程は線形予測理論で重要な役割を果たす確率過程である。

マルコフ過程

確率過程｛X_t（ω）｝において，時刻tでの値X_t（ω）を知れば，t以前の結果とt以後の事象とが互いに独立になるとき，｛X_t（ω）｝をマルコフ過程という。ランダムウォーク，ポアソン過程，ウィーナー過程はすべてマルコフ過程で解析学と深い関連をもち，応用上も重要である。
執筆者：野本 久夫

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

確率過程
かくりつかてい

円の交換レート、ある地区における降雨量、通信工学における雑音現象、ブラウン運動などは、時の経過に伴って偶然性をもって変動する現象である。このような現象の数学的モデルが確率過程である。数学的にいえば、実数tをパラメーターとする確率変数族｛X_t｝を確率過程という。ここでtを固定すればX_tは確率変数であるが、X_tの標本空間Ωはtに無関係で一定のものである。X_tはtとΩの元ωの関数であるから
　　X_t＝X(t,ω)
と表される。Ωの元ωを固定するとX(t,ω)はtの関数となるが、この関数を標本関数または道とよぶ。

　任意に有限個の実数t₁、t₂、……、t_nを選んで、k次元確率変数(X_t1,X_t2,……,X_tk)を考え、このk次元確率変数の確率分布を確率過程｛X_t｝の有限次元分布という。確率過程はその有限次元分布の性質によって、加法過程、マルコフ過程、定常過程などに分けられる。区間I＝(a,b)に対して確率変数X_Iを
　　X_I＝X_b－X_a
と定める。互いに重なり合うことのない区間
　　I,J,……,K
に対して、確率変数
　　X_I,X_J,……,X_K
が独立であるとき、確率過程｛X_t｝を加法過程という。

　加法過程において、標本関数がtの連続関数であるようなω全体の確率が1であるとき、確率変数X_t－X_s(t＞s)の確率分布は正規分布となる。このような確率過程を正規加法過程という。ここでとくにX_t－X_sの平均値が0で、分散がt－sであるとき、この確率過程をウィーナー過程またはウィーナーのブラウン運動という。また、標本関数が高さ1の飛躍で増加するような階段関数であるようなω全体の確率が1であるとき、確率変数X_t－X_sの確率分布はポアソン分布である。このような確率過程をポアソン過程という。

　次に、時間とともに変化する偶然的現象において、時刻sにおける状態がわかっているとき、時刻t(t＞s)における状態が、時刻sにおける状態だけで決まり、s以前の状態には無関係なことがある。このような性質をもつ確率過程をマルコフ過程という。詳しくいえば、｛X_t｝を確率過程とするとき、
　　s₁＜s₂＜……＜s_n＜t
としてX_s1、X_s2、……、X_sn、X_tの値を与えたときのX_tの条件つき確率法則が、X_snの値だけを与えたときのX_tの条件つき確率法則に等しいとき、すなわち
　　P(X_t(ω)∈A|X_s1＝x_s1,……,X_sn＝x_sn)
　　＝P(X_t(ω)∈A|X_sn＝x_sn)
が成り立つとき｛X_t｝をマルコフ過程という。

　マルコフ過程の確率法則はs≦tとしてX_s＝xのときのX_tの条件つき確率F(s,x;t,A)によって決定される。この確率を遷移確率という。

［古屋　茂］

『伊藤清著『現代数学14　確率論』（1953・岩波書店）』

[参照項目] | 確率変数 | 定常過程

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

確率過程
かくりつかてい
stochastic process

変量の時間変化が偶然に支配され，ある確率に従って起る過程。このような変量 X を確率変数といい，時刻 t におけるその観測値を X(t) とするとき，確率過程は観測時刻 t の集合 T における X(t) の集合 {X(t)｜t∈T} で定義される。 X(t₁) ，X(t₂) ，…の確率分布の特性によって，マルコフ過程，定常過程などに分類される。 t の変動が整数値 t＝0 ，±1 ，±2 ，…だけをとって行われるときは離散型確率過程，連続的に行われるときは連続型確率過程という。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の確率過程の言及

【ドゥーブ】より

…1935年以来イリノイ大学に所属し，45年教授となる。確率過程論の基礎に関する系統的研究を行い，とくに可分変形の理論とマルチンゲールの理論は著しく，その成果は53年刊行の著書《確率過程》に収められている。マルチンゲールは公平なかけ事のモデルと考えられる重要な確率過程であり，P.レビらが研究を始めたが，ドゥーブはそれとともに劣マルチンゲールという概念も導入し，解析学における(劣)調和関数論の確率論版ともいうべき美しい理論を作った。…

【数理統計学】より

…また，母集団がいくつかの層に分かれているとき，適当なウェイト(重み)で標本の層別抽出を行うことは正確さを増すうえで重要なことである。
［時系列の解析］
　時間とともに変化する偶然現象を時系列，または確率過程という。例えば気温は季節的な変動のほかに偶然に支配されて刻々と変動している。…

【非線形力学】より

…元来，方程式(1)または(2)ではある時刻における変数xの値が与えられたとき，それ以後の時刻でのxは一義的に定まるはずで，〈決定論的力学〉と呼ばれるものである。これに対し，実在するランダム力(ノイズ)によって駆動される力学系で軌道が確率的にしか定められないものもあり，〈確率過程〉と呼ばれているが，カオスの現象は決定論的力学の中にあたかも外見上確率過程と同じ様相を呈するものがあるということを意味し，自然法則の決定性と蓋然性との橋渡しをしているという意味で，現代非線形力学の一つの中心課題となっている。図5-bに見られるヘノン=ハイレス系のポアンカレ写像の不規則点は保存力学系カオスの典型例である。…

※「確率過程」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」