ぎゃくこうし
逆格子
reciprocal lattice
3個の独立なベクトルをa, b, cとし,p, q, rを整数とするとき,原点からr=pa+qb+rcなる点のつくる点列はa, b, cを基本ベクトルとする三次元格子をつくり,これを実格子といい,a, b, cの逆ベクトルa*, b*, c*を基本ベクトルとする格子を逆格子という。
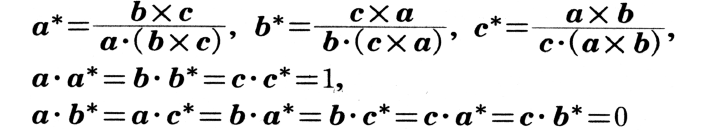
なる関係にあり,これより,
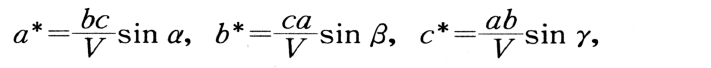
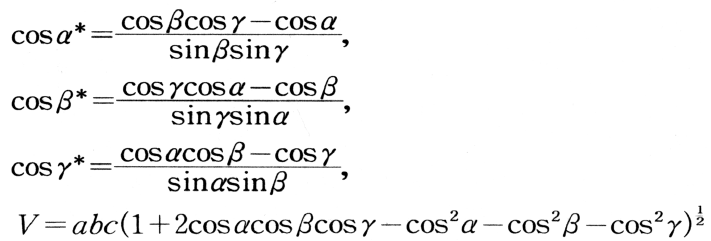
を得る。結晶によるX線回折においては,逆格子点Sがエワルドの反射球面上に位置するとき回折線が現れる。*, *, *を用いて表したSの座標(hkl)は,その逆格子点に対応するブラッグ反射の次数がnであるとすると,(h/n, k/n, l/n)が反射面のミラー指数に等しいという関係にある。
執筆者:丸茂 文幸
出典 平凡社「最新 地学事典」最新 地学事典について 情報
Sponserd by 
逆格子
ギャクコウシ
reciprocal lattice
結晶によるX線の回折現象.とくに回折の幾何学を系統的に理解するために,P.P. Ewald(1921年)によって導入された概念.基本周期a,b,cの空間格子に対し,次式で定義される基本周期 a*,b*,c* をもつ空間格子をもとの格子(実格子)の逆格子という.
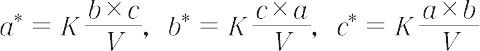
ここで,V( = a・b × c)は単位格子の体積,Kは定数で,1,λ(波長)または2πである.定義より,
a・a* = b・b* = c・c* = K,
a・b* = … = c・b* = 0.
また,h,k,lを整数とするとき,逆格子ベクトル
Hhkl = ha* + kb* + lc*
は格子面(hkl)に垂直であり,
|Hhkl|=K/dhkl
である.ただし,dhkl は面(hkl)の面間隔.逆格子を用いるとラウエ条件は,K = λとしたとき,
Hhkl = s - s0 = S
と書ける.ここで,s0 は入射X線,sは回折X線を表す単位ベクトルで,Sは散乱ベクトルとよばれる.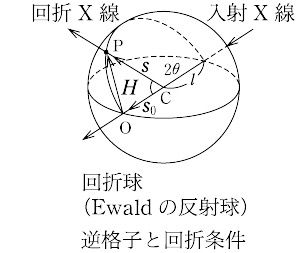 すなわち,図に示すように,面(hkl)の逆格子点PがEwaldの反射球(または回折球)上にあれば,
すなわち,図に示すように,面(hkl)の逆格子点PがEwaldの反射球(または回折球)上にあれば, 方向に回折X線が生じる.
方向に回折X線が生じる.
Cは結晶試料の位置,Oは逆格子の原点である.逆格子と反射球との関係は,結晶と入射X線との関係に対応している.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
Sponserd by 
逆格子
ぎゃくこうし
reciprocal lattice
空間格子の基本ベクトルを a1,a2,a3 としたとき,
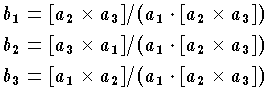 を基本ベクトルとする空間格子を逆格子という。逆格子の格子点はもとの空間格子の格子面に対応する。すなわち逆格子の格子点 (hkl) はもとの空間格子の格子面 (hkl) の法線上に原点から 1/d の位置にある ( d は面間隔) 。単純格子,底心格子,体心立方格子,面心立方格子の逆格子は,それぞれ単純格子,底心格子,面心立方格子,体心立方格子である。逆格子は結晶によるX線回折や結晶内の電子状態など,結晶内の波動を記述するのに用いられる。
を基本ベクトルとする空間格子を逆格子という。逆格子の格子点はもとの空間格子の格子面に対応する。すなわち逆格子の格子点 (hkl) はもとの空間格子の格子面 (hkl) の法線上に原点から 1/d の位置にある ( d は面間隔) 。単純格子,底心格子,体心立方格子,面心立方格子の逆格子は,それぞれ単純格子,底心格子,面心立方格子,体心立方格子である。逆格子は結晶によるX線回折や結晶内の電子状態など,結晶内の波動を記述するのに用いられる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
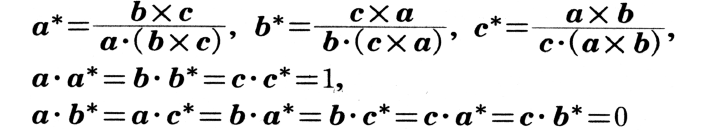
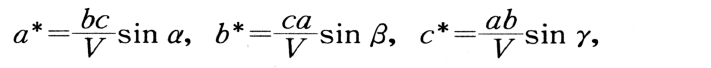
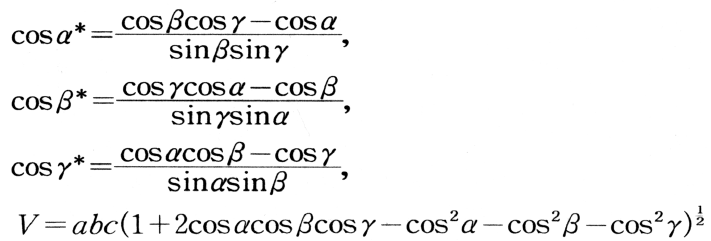


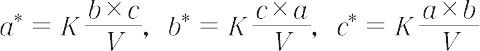
 すなわち,図に示すように,面(hkl)の逆格子点PがEwaldの反射球(または回折球)上にあれば,
すなわち,図に示すように,面(hkl)の逆格子点PがEwaldの反射球(または回折球)上にあれば, 方向に回折X線が生じる.
方向に回折X線が生じる.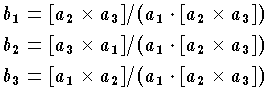 を基本ベクトルとする空間格子を逆格子という。逆格子の格子点はもとの空間格子の格子面に対応する。すなわち逆格子の格子点 (hkl) はもとの空間格子の格子面 (hkl) の法線上に原点から 1/d の位置にある ( d は面間隔) 。
を基本ベクトルとする空間格子を逆格子という。逆格子の格子点はもとの空間格子の格子面に対応する。すなわち逆格子の格子点 (hkl) はもとの空間格子の格子面 (hkl) の法線上に原点から 1/d の位置にある ( d は面間隔) 。