重なり積分（読み）カサナリセキブン

化学辞典 第2版

重なり積分
カサナリセキブン
overlap integral

二つの軌道関数の重なりの大きさを表す積分．ψ_a，ψ_b を軌道関数とすると，重なり積分 S_ab は次式で与えられる．

S_ab ＝ ∫ ψ_a^*ψ_bdτ

ここで，ψ_a^* は ψ_a の複素共役な関数であり，積分は全空間にわたって行われる．二つの軌道関数が同一の場合(ψ_a ＝ ψ_b)，重なりは完全であり，S_aa ＝ 1となる．ψ_a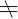ψ_b の場合，S_ab の値は1より小さい．この場合，S_ab の大きさは，それらの軌道によってつくられる結合の強さを判定する基準となる．たとえば，ψ_a と ψ_b が直交しているときは S_ab ＝ 0であり，ψ_a，ψ_b の間の結合は生じない．分子軌道法による計算においては，重なり積分は ψ_a ＝ ψ_b 以外は無視されることが多い．つまり，S_aa ＝ 1，S_ab ＝ 0とおいた重なり積分無視の近似がとられる．

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

重なり積分
かさなりせきぶん
overlap integral

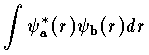水素分子のような二原子分子に対して，それぞれの原子核のまわりの2原子の波動関数を ψ_a ，ψ_b とし，位置座標を r とするとき， を重なり積分といい，ψ_a と ψ_b の重なりの程度を表わす量になる。重なり積分は，一般にはゼロでない値をもつが，特にゼロになるとき，2つの波動関数は直交するという。ハイトラー＝ロンドンの理論では，二原子分子の波動関数を ψ_a ，ψ_b の一次結合によって近似するから，物理量の計算において常に重なり積分が現れ，この積分がゼロでないことによって，計算が困難になる。しかし，大きな分子や磁気などを量子力学的に扱うときは，重なり積分を無視して計算を行なっても，実験値と一致する場合がかなりよくあることも知られている。

出典　ブリタニカ国際大百科事典 小項目事典