分子軌道法（読み）ブンシキドウホウ（その他表記）molecular orbital method

デジタル大辞泉

ぶんしきどう‐ほう〔ブンシキダウハフ〕【分子軌道法】

分子内の電子の運動状態を、分子全体に広がった分子軌道で表せると仮定し、着目する電子の波動関数の重ね合わせによって電子の状態を近似的に求める手法。量子化学や計算化学の分野で広く用いられ、コンピューターの性能向上に伴い、複雑な分子の反応や構造を計算できるようになった。分子軌道関数法。MO法。

出典　小学館

改訂新版　世界大百科事典

分子軌道法 (ぶんしきどうほう)
molecular orbital method

MO法と略称され，分子軌道関数法ともいう。分子の電子状態を取り扱う量子化学の理論的方法の一つ。分子軌道法では，分子内の電子が一般に，分子を構成するすべての原子の周囲に広がった電子軌道にはいっていると仮定する。上に述べたような電子軌道を分子軌道という。水素分子を例にとって，この方法の基本的性格を説明すると次のようである。水素原子は1s軌道に1個の電子をもっている。したがって，水素分子H₂は合計2個の核外電子をもつことになるが，分子軌道法では，2個の水素原子核の周囲に広がった分子軌道にそれらの電子がはいっているものと考える。

　分子軌道を具体的に計算するには，いろいろな理論的手法があるが，最も普通に用いられる近似は，原子軌道の1次結合で分子軌道を表す手法であり，これをLCAO近似という（LCAOはlinear combination of atomic orbitalsの略）。水素分子を構成する2個の水素原子をそれぞれa，bと符号をつけて，おのおのの1s軌道をφ_a，φ_bと表すと，LCAO近似による分子軌道は，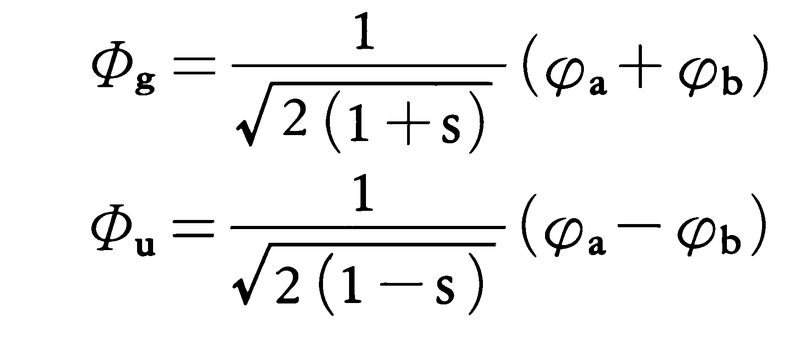

と表現できる。上の式でsはφ_aとφ_bの重なり積分で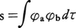，である。上記の二つの分子軌道の中で，Φ_gのほうがΦ_uより安定であり，それぞれの分子軌道はスピンの異なる2個の電子を収容できるので，水素分子の基底状態では，2個の電子がいずれもΦ_g軌道にはいる。電子に1，2と符号をつけると，水素分子の基底状態を表す波動関数Ψ₀はΦ_g（1）Φ_g（2）と表現できる。前に示したΦ_gの式を用いると，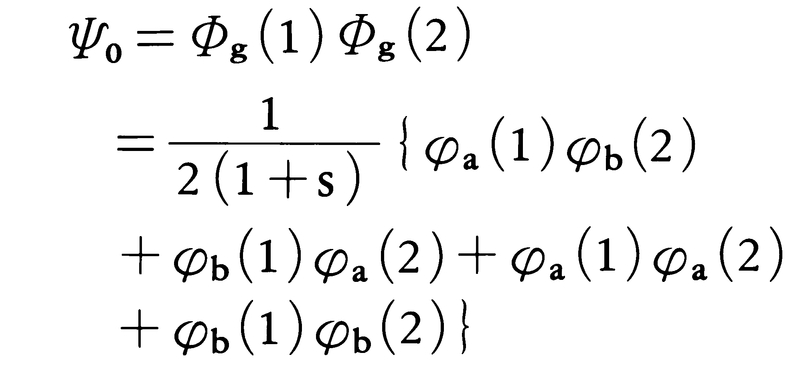

となる。この波動関数を原子価結合法による水素分子の波動関数と比較すると，かっこ内の最初の2項が原子価結合法における共有結合状態の波動関数に，残りの2項がH⁺……H⁻のようなイオン結合状態の波動関数に対応するので，分子軌道法における波動関数では共有結合的な状態とイオン結合的な状態とが等価に考慮されていることがわかる。これはイオン結合の寄与を過大に評価することになり，適切ではない。分子軌道法では，その出発点において，電子間の反発の効果が取り込まれていないために，このような結果になるのである。上述の欠点を克服するには，Φ_g（1）Φ_g（2）なる基底電子配置と，Φ_g（1）Φ_u（2），Φ_u（1）Φ_g（2），Φ_u（1）Φ_u（2）などの励起電子配置の混ざり合い（配置間相互作用）を考慮する方法がとられる。核外電子の相互作用の影響を電子が感ずるポテンシャルの中に取り入れる方法に自己無撞着場の方法があるが，その方法を用いて分子軌道を計算したうえで，配置間相互作用を十分に取り入れた計算を行うと，経験的な数値をまったく用いることなしに，信頼度の高い計算結果を得ることができる。このような非経験的分子軌道法ab initio molecular orbital methodによる理論計算は，高速コンピューターの利用によって，多原子分子についても行われるようになっている。しかし，原子数が増加すると，上記の方法を用いるのが困難になるので，価電子のみを考慮し，また，計算上必要になる積分値などに経験的な数値を用いる半経験的分子軌道法を用いることが多い。これには，近似の性格が異なるいくつかの方法が知られているが，代表的なものとしては，拡張HMO法やCNDO法と呼ばれるものがある。π電子共役系をもつ分子については，π電子近似の半経験的分子軌道法が用いられる。この方法では，π電子以外のすべての電子の効果をπ電子が感ずるポテンシャルの中に取り入れるだけにして，π電子の軌道のみを計算する。
執筆者：黒田 晴雄

出典　株式会社平凡社「改訂新版　世界大百科事典」

化学辞典 第2版

分子軌道法
ブンシキドウホウ
molecular orbital method

略称MO法．分子の電子状態を定める近似法の一種．これに対して，原子軌道法(AO法)または原子価結合法(VB法)とよばれる近似法がある．多電子系の分子にシュレーディンガーの波動方程式を適用しても，多体問題や多中心の問題が加わって解くことはできない．そのため，いろいろな近似方法が行われているが，それらの考え方の出発点となっているものがMO法とAO法に大別される．どちらも分子軌道関数は，普通，原子軌道(原子の波動関数)によって組み立てられる．AO法では，電子は構成原子に強く束縛されているという立場から分子を考えるのに対して，MO法では，電子は原子から解放されて分子全体に広がっていると考える．このように，AO法では構成原子の個性を重視するが，MO法ではこれを無視する．
しかし，どちらの方法から出発しても，近似を高めていけばよく一致した結論が得られる．MO法では分子全体に広がっている軌道が，原子に近いところではその原子軌道に似た形となるとして，分子軌道をしばしば構成原子の原子軌道(AO)の線形結合として近似する．これをLCAO近似という．分子軌道(MO)の数は用いたAOの数と等しいが，各MOはパウリの原理によってスピン逆平行の電子を2個まで収容できる．基底状態はエネルギーの低い順にMOに2個ずつ電子を入れることによって与えられる．たとえば，水素分子では結合性分子軌道にスピン逆平行の2個の電子が入って基底状態がつくられる．この場合，電子は分子全体に広がって運動しているので，2個の電子が同時に一方の原子に集まる確率が生じ，イオン構造の寄与が過大に見積もられる結果になる．これを補正するために，ほかの状態(励起状態)を取り入れる方法が用いられる．これを配置間相互作用(CI)の近似という．
LCAO近似のMO法のなかで，CIをあらわに考慮しないもっとも簡単な方法として用いられるものに，ヒュッケル(Hückel)近似がある．この方法の特徴は，まず多電子系のハミルトニアンを，各電子に電子間相互作用を均等にわりあてて，有効な一電子ハミルトニアンの和として表す．次に，このようにして得られる行列要素を見積もるのに，炭化水素のπ電子系の場合，クーロン積分と共鳴積分を経験的なパラメーターとみなし，実測値を再現するように決める．ヒュッケル法は定量的な研究には向かないが種々の分子を比較検討する場合に有効である．
ヒュッケルMO法はπ電子系だけに適用されるが，σ電子系を扱う拡張されたヒュッケル法(extended Hückel method)がある．この方法では，内殻電子(1s電子)を除くすべての原子軌道を用いてLCAO-MOをつくり，クーロン積分は原子価状態のイオン化電位で見積もり，共鳴積分はクーロン積分と重なり積分から計算される．電子間相互作用をあらわに考慮したMO法は反対称化分子軌道(ASMO)法とよばれる．ASMO法では，スピン関数を含めた全系の波動関数がパウリの原理を満足するように反対称化されている．一般に，対称性の高い特別の分子を除いては，LCAO-MOのなかのAOの係数をはじめから知ることはできない．このような場合，ハートリー-フォック(Hartree-Fock)の自己無撞(どう)着場(selfconsistent field，SCF)の方法と同様の手続きでMOが決められている．LCAO-ASMO-SCF法による理論的な計算結果は，信頼できると思われるAOを用いても実測結果とはかなりの差を生じる．そこで，原子積分を経験的な値を用いて評価し，実験値との一致をはかる方法として提案された半経験的な方法であるパリザー-パール-ポープル(Pariser-Parr-Pople，PPP)法が利用される．この方法では，一中心クーロン積分を実測による原子価状態のイオン化電位から電子親和力を引いた値として定める．PPP法が現在広く利用され，MO計算の標準的な方法になっている．

出典　森北出版「化学辞典（第2版）」

日本大百科全書(ニッポニカ)

分子軌道法
ぶんしきどうほう
molecular orbital method

分子の中の電子の状態を明らかにする理論計算法の一つ。普通、略してMO法ともHMH（Hund-Mulliken-Hückel）法ともいい、また分子軌道関数法ともいう。分子内の電子はどうして化学結合を形成するかの理論は、歴史的にはドイツのハイトラーとアメリカ（ドイツ生まれ）のF・ロンドンの導いた原子価結合法（valence-bond method、略称VB法、原子軌道関数法ともいう）である。

　MO法においては電子の波動関数を分子全体に広がった関数ととるので（これをMO、分子軌道関数という）この名がある。別の表現を用いると「融合原子核」方式といい、電子が融合原子核の周りを動くと考えた波動関数を採用する。水素分子を例にとり、VB法とMO法を比較すると、VB法では水素分子に対する波動関数を、
　　Ψ＝Ψ_A(1)Ψ_B(2)＋Ψ_A(2)Ψ_B(1)
ととるのに対し、MO法では、
　　Ψ＝｛Ψ_A(1)＋Ψ_B(2)｝
　　　　　　　　　｛Ψ_A(2)＋Ψ_B(1)｝
ととる。したがってMO法ではΨ_A(1)Ψ_A(2)と、Ψ_B(1)Ψ_B(2)のようなイオン項が含まれている。ハミルトニアン（量子力学においてシュレーディンガーの波動方程式に用いる演算子）は、VB法でもMO法でも等しく、また両方法とも二つのエネルギー値が求められる。そのうち、一方が結合軌道、他方が反結合軌道であり、水素分子の形成が量子力学によって説明された。

　ドイツのヒュッケルは、共役二重結合をもつ化合物について、そのπ(パイ)電子をMOにとり、紫外吸収スペクトルの測定値を説明することに成功した。π電子にのみ注目したMO法は、単純ヒュッケル法（HMO法）とよばれる。今日、これにσ(シグマ)電子を加えたり、波動関数を修正したりしてさまざまのMO法が開発されている。CNDO法（complete neglect of differential overlap）、INDO法（intermediate neglect of differential overlap）などがその例である。

　MO法により、分子内の電荷密度、結合次数、自由原子価などが求められ、炭素化合物の反応性、立体配座などが理論的に説明できるようになった。また、分子の励起状態を計算から求め、蛍光、リン光の機構の説明、反応中間体の分子構造も理論的に予測することもできるようになりつつある。

［下沢　隆］

『原田義也著『基礎化学選書12　量子化学』（1978・裳華房）』▽『米沢貞次郎他著『量子化学入門』上下（1983・化学同人）』▽『藤永茂著『入門　分子軌道法――分子計算を手がける前に』（1990・講談社）』▽『広田穣著『化学新シリーズ　分子軌道法』（1999・裳華房）』▽『武次徹也・平尾公彦著『早わかり分子軌道法』（2003・裳華房）』▽『平山令明著『実践　量子化学入門――分子軌道法で化学反応が見える』（講談社・ブルーバックス）』

[参照項目] | ハイトラー‐ロンドンの理論 | ハミルトニアン

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

分子軌道法
ぶんしきどうほう
molecular orbital method

MO法と略記する。量子力学的に分子の電子状態を解明するのに用いられる近似理論であり，R.S.マリケン，W.ヒュッケルによって確立された。分子の電子状態はシュレーディンガーの波動方程式によって解明できるはずであるが，複雑な分子においては完全な解明は不可能であり，なんらかの近似理論が必要である。この要請にこたえるものとして W.ハイトラーと F.ロンドン，J.C.スレーターと L.C.ポーリングによる原子価結合法 (VB法) があり，次いで現れたのがこの MO法である。この原理は分子全体に広がるオービタルを各電子が運動していると考えるもので，複雑な分子の取扱いが VB法よりも容易なため，近年大きく発展した。特に複雑な有機化合物を取扱う場合には，π電子だけの分子軌道の情報を引出す方法として電子近似法があり，最も単純なものとしてヒュッケルの MO法がある。さらに近似を進めたものに拡張ヒュッケル法，SCF法などが知られており，電子計算機の発展のため手軽に計算ができるようになった。現在では MO法は量子化学の基礎となる理論であるばかりでなく，それから得られる電子状態の情報は反応・構造有機化学者にとって必須のものである。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

分子軌道法【ぶんしきどうほう】

分子中の電子の状態（分子軌道）を量子力学的な計算によって求め，その分子の構造や化学反応などに関する特性を理論的に調べる量子化学の手法。ふつう，分子を構成する各原子の電子波動関数（原子軌道）をもとに，重ね合わせの原理を用いて近似されることが多い。最もエネルギー準位の高い分子軌道に着目し，その電子（フロンティア電子）が化学反応などに重要な役割を果たすことを示した福井謙一の〈フロンティア電子理論〉は有名。現在ではコンピューターを用いた複雑な計算が可能になり，かなり大きな分子にまで適用範囲が広がっている。
→関連項目ホフマン

出典　株式会社平凡社

世界大百科事典（旧版）内の分子軌道法の言及

【化学結合】より

…この理論は，化学者の経験から導かれた原子価の概念や分子構造式との対応がよく，原子価結合法として発展した。　この原子価結合法に対してもう一つの理論として，電子は分子全体に広がる軌道(分子軌道)の上を運動するとして扱う分子軌道法がその後導入された。この方法では分子軌道の波動関数φを構成原子の波動関数の一次結合で近似することが多い。…

【原子価結合法】より

…この理論では，分子内の価電子は個々の原子に固有な原子軌道に属している状態に近いものと考えられるので，この理論は原子軌道法atomic orbital method，略してAO法とも呼ばれている。これに対し，分子軌道法(MO法)では，価電子は個々の原子軌道から離れて，分子全体に広がる分子軌道に属していると考えることから出発している。　VB法で水素分子の結合機構を説明すると，つぎのようになる。…

【有機化学】より

…相次いで導入された質量分析法，核磁気共鳴スペクトル法が有機化学者の強力な武器となり，有機化学の飛躍的な発展の原動力となった。それより先，ヒュッケルErich Armand Arthur Joseph Hückel(1896‐1980)は分子軌道法を有機化学に導入した。ヒュッケル分子軌道法はきわめて粗い近似を用いたものではあったが，それまで水素分子といったごく簡単な分子にしか適用できなかった量子力学を有機化学の世界に持ち込んだ点に画期的な意義がある。…

※「分子軌道法」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」