精選版 日本国語大辞典 「二次関数」の意味・読み・例文・類語
にじ‐かんすう‥クヮンスウ【二次関数】
- 〘 名詞 〙 独立変数の二次式で表わされる関数。すなわち、y=ax2+bx+c (a
 0)という形のもの。グラフは放物線となる。
0)という形のもの。グラフは放物線となる。
日本大百科全書(ニッポニカ) 「二次関数」の意味・わかりやすい解説
二次関数
にじかんすう
a、b、cを定数とするとき、
y=ax2+bx+c (a≠0)
で表される関数をいう。とくに、定数bとcがともにゼロであれば、yはxの二乗(平方)に比例する。たとえば、ボールを地上hメートルのところから、毎秒v0メートルの速さで真上に投げ上げるとき、x秒後のボールの高さを地上yメートルとすれば、だいたいy=-4.9x2+v0x+hが成り立つ。
以下、この関数の定義域は実数全体の集合とし、a、b、cもすべて実数とする。いわゆる「平方完成」によって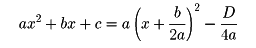
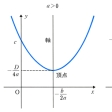
と変形できる。ただしD=b2-4acである。この関数のグラフは、放物線y=ax2をx軸の方向に-b/2aだけ、y軸の方向に-D/4aだけ平行移動したものである。したがって、このグラフは、頂点が(-b/2a,-D/4a)、軸(対称軸)がx=-b/2aである放物線となる。また、a>0のとき、グラフは下に凸であるから、この関数はx<-b/2aで減少、x>-b/2aで増加し、x=-b/2aで最小値-D/4aをとる。a<0のときには、増減がこれとは逆になり、x=-b/2aで最大値-D/4aをとる。また、yの値がゼロになるときのxの値は、二次方程式ax2+bx+c=0の解であるから、D>0のとき、二次関数y=ax2+bx+cのグラフはx軸と2点で交わり、D=0のときにはx軸と接し、D<0のときはx軸と共有点をもたない。
[植竹恒男]
改訂新版 世界大百科事典 「二次関数」の意味・わかりやすい解説
二次関数 (にじかんすう)
quadratic function
xの二次式で表される関数y=ax2+bx+c(a,b,cは実数)を二次関数という。y=ax2+bx+cのグラフは図1の形の放物線である。これはy=ax2のグラフをx軸方向に-\(\frac{b}{2a}\),y軸方向に-\(\frac{b^2-4ac}{4a}\)
だけ平行移動したものであり,直線x=-\(\frac{b}{2a}\)に関して対称である。二次関数は,a>0,a<0に応じてx=-\(\frac{b}{2a}\)のとき,それぞれ最小値,最大値をとり,その値は-\(\frac{b^2-4ac}{4a}\)である。
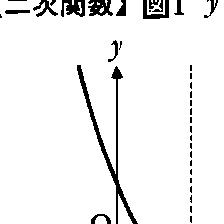
二次関数は,自然現象を記述するときにも現れる。例えば,物体を初速vで投げ上げたとき,重力の加速度をgとして,空気の抵抗が無視できるならば,x秒後における物体の地上からの高さyは,
y=vx-\(\frac{1}{2}\)gx2
と二次関数で与えられる。この場合,グラフは図2のように座標原点を通る。また,このグラフから物体は時刻v/gで最高点に達すること,2v/g秒後に地上に落下することなどがわかる。
執筆者:杉江 徹
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「二次関数」の意味・わかりやすい解説
二次関数【にじかんすう】
→関連項目二次曲面
出典 株式会社平凡社百科事典マイペディアについて 情報
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...