分数方程式（読み）ぶんすうほうていしき

精選版 日本国語大辞典

ぶんすう‐ほうていしき ‥ハウテイシキ【分数方程式】

〘名〙 二つの分数式を等号でつないで得られる方程式。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

分数方程式
ぶんすうほうていしき

未知数についての分数式を含む方程式を分数方程式という。いかなる形の分数方程式も等式変形によってf(x)/g(x)=0の形に書かれる。ここでf(x),g(x)はxの整式でg(x)は恒等的にゼロではない。この方程式の根(こん)をαとすると、f(α)/g(α)=0だから、f(α)=0かつ、g(α)≠0でなければならない。したがって分数方程式f(x)/g(x)=0を解くには、まず整方程式f(x)=0を解き、次にこの根のうちで分母をゼロにしないものを選ぶ（根の吟味）。これら根のうちで分母をゼロにするものを無縁根という。言い換えれば無縁根は分子、分母をそれぞれゼロとおいて得られる二つの方程式の共通根である。たとえば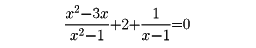

を解くのに、通分して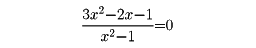

となり、二次方程式3x²-2x-1=0を解いて二根1と-1/3を得る。ところが1は分母をゼロにするから無縁根である。分母のxに-1/3を代入すると値-8/9を得る。したがって求める根は-1/3である。

　もしf(x)/g(x)が既約、つまりf(x)とg(x)が公約数をもたないときは、方程式の解法で無縁根は現れないことがわかる。たとえば、前の例で、分母分子をその最大公約数x-1で約分して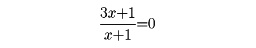

とすれば、根-1/3だけが得られる。方程式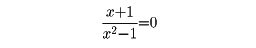

のように無縁根しかないときは、この方程式は不能（根をもたない）である。

［竹内芳男］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

分数方程式 (ぶんすうほうていしき)
fractional equation

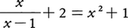のように分数式を含む方程式。分数方程式を解くには，分母を払って代数方程式を導き，それの根のうちで分母を0にしないものを求めればよい。分母を0にするものは分数方程式の無縁根と呼ばれる。分数方程式，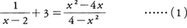

を解いてみよう。両辺に4－x²をかけて整理すると，

　4x²－3x－10＝0

を得，この方程式の根として，x＝2，－5/4を得る。このうちx＝2は方程式（1）の分母を0にするので無縁根であり，求める根は－5/4である。

　分数方程式を解くためには上記のやり方のほかに次の方法がある。方程式のすべての項を左辺または右辺に移し，通分した結果を既約分数式に直し，その分子＝0という方程式を解くとその根が最初の分数方程式のすべての根を与える。このときは無縁根は現れない。通分した際の分母と分子の共通因子＝0の根が最初の方法で解いたときの無縁根を与える。分数方程式（1）をこの方法で解いてみよう。（1）の右辺を左辺に移項して通分すると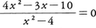，を得る。これを既約分数式に直すと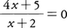，が得られ，求める根は－5/4であることがわかる。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

分数方程式
ぶんすうほうていしき
fractional equation

たとえば
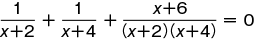のように，未知数についての分数式を含む方程式を分数方程式という。分数方程式を解くには，分母をはらって得られる方程式を解けばよいが，そうして得られた値が，必ずしももとの分数方程式の根となるとはかぎらない。

出典　ブリタニカ国際大百科事典 小項目事典