三次方程式（読み）サンジホウテイシキ

デジタル大辞泉

さんじ‐ほうていしき〔‐ハウテイシキ〕【三次方程式】

未知数の最高次数が三次である方程式。ax³＋bx²＋cx＋d＝0（a≠0）の形にすることができる方程式。

出典　小学館

精選版 日本国語大辞典

さんじ‐ほうていしき‥ハウテイシキ【三次方程式】

1. 〘 名詞 〙 未知数の最高羃(べき)が三次であるような整方程式。ax³+bx²+cx+d=0 （a, b, c, d は定数、a0）の形に整理することのできる方程式。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

三次方程式
さんじほうていしき

次の形の式を三次方程式という。

　　(1) a₃x³＋a₂x²＋a₁x＋a₀＝0
　　　　　　 (a₃≠0)
(1)を満たす複素数（実数の場合を含む）xをこの方程式の根といい、根を求めることを三次方程式を解くという。(1)の両辺をa₃で割り、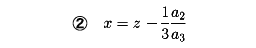

と置くと、2乗の項のないzの三次方程式
　　(3)　z³＋3pz＋q＝0
を得る。ここでp、qは(1)式の係数で書くことができ、(1)を解くことと(2)を解くことは同値になる。いま、(3)の根をz₁、z₂、z₃とすると、
　　D＝(z₁－z₂)²(z₁－z₃)²(z₂－z₃)²
　　　　＝－27(4p³＋q²)
となる。このDを三次方程式(3)の判別式という。(3)が重根をもつ必要十分条件はD＝0であり、とくにp、qが実数のとき、D≧0なら(3)の根はすべて実数で、D＜0なら(3)は一つの実根と、互いに共役な二つの虚根をもつ。

　一般に三次方程式(3)は次の方法で解ける。z＝u＋vと置くと、(3)は
　　(u³＋v³＋q)＋3(u＋v)(uv＋p)＝0
となるから、連立方程式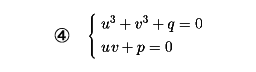

を満たす一つの解u、vを求めると、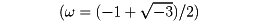

が求める(3)の根である。一方、(4)の解は、vを消去すると
　　(u³)²＋qu³－p³＝0
となるから、求めるu、vは

で得られる。この方法は16世紀イタリアの数学者カルダーノによって発見された。四次方程式も三次方程式に帰着して解けるが（フェラリによる）、五次以上の高い次数の代数方程式にはこの種の代数的解法は存在しない（アーベルによる）。

［菅野恒雄］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

三次方程式【さんじほうていしき】

a（≠０），b，c，dを定数としてax³＋bx²＋cx＋d＝０と書き表される方程式。x＝y−（b/3a）とおきy³＋３py＋q＝０の形に変え，t²＋qt−p³＝０の２根をt₁，t₂とすればyの値は（式１）となる（ω，ω²は１の立方根でそれぞれ（式２））。これをカルダーノの解法という。→タルタリア／二次方程式／四次方程式
→関連項目方程式

出典　株式会社平凡社

世界大百科事典（旧版）内の三次方程式の言及

【王孝通】より

…著書に《算経十書》の一つ《緝古算経（しゆうこさんけい）》がある。問題は全部で20術収められており，そのうちの19術までが開帯従立方法(三次方程式の正根を求める方法)を利用して，堤防などの体積を求める問題，および複雑な勾股（こうこ）問題(直角三角形におけるピタゴラスの定理の応用)を解く方法を説いたものであり，三次方程式を解いた最古の数学書である。彼が立てた帯従立方開方式つまり三次方程式x³＋px²＋qx＝rの係数はすべて具体的な正の数で，q＝0の場合も含まれている。…

【カルダーノ】より

…イタリアの医学者，自然哲学者，数学者。占星術や魔術にも造詣が深かった。法律家で，数学にもたしなみのあったF.カルダーノの庶出児としてパビアに生まれた。1526年にパドバ大学で医学博士となり，開業したが，初めの10年近くはほとんど患者もつかず，極貧の生活を送った。また青年時代には長らく性的に不能であった。しかしその後しだいに名医としての評判が高まり，ミラノ，パビア，パドバの各大学で医学教授を歴任するかたわら，有力な貴族たちから診察を求められた。…

※「三次方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」