解析学（読み）カイセキガク（英語表記）analysis

デジタル大辞泉

かいせき‐がく【解析学】

微分積分学とそれから発展した数学の諸分科の総称。微分積分学・微分方程式論・積分方程式論・実関数論・複素関数論など。

出典　小学館

精選版 日本国語大辞典

かいせき‐がく【解析学】

1. 〘 名詞 〙 微積分学、ならびにそれから発展した諸分野の総称。代数学、幾何学に対していう。微積分学、微分方程式論、積分方程式論、実関数論、複素関数論などが含まれる。
   1. [初出の実例]「彼女は併し、解析学の教科書を擲つよりも容易に私を擲った」(出典：軍艦茉莉（1929）〈安西冬衛〉五)

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

解析学
かいせきがく
analysis

代数学、幾何学と並んで、数学を大きく分けたときの一つの分野。極限概念を基礎とする。級数論、微分積分法、複素関数論、フーリエ解析、関数解析、微分方程式論、積分方程式論、変分法などの総称。

［竹之内脩］

ギリシア時代から17世紀まで

極限概念のおこりは古く、紀元前400年ごろのエウドクソスにまでさかのぼる。ユークリッドの『原本』（ストイケイア）で、円錐(えんすい)、角錐の体積を求めているが、これはエウドクソスによるものである。その後、アルキメデスは前250年ごろ、放物線とその一つの弦で囲まれた部分の面積、球の表面積、体積などを与えている。これらギリシアの数学者は、求める量Sがある値Aであることを証明するために、量Sを近似する列をつくった。それを用いて、|S－A|がゼロに収束するようなある数列のどの項よりも小さいから、ゼロでなければならないとした。これは、「取りつくし法」とよばれている。その議論は幾何学的で、まことに厳格なものだったが、以後しばらくはその研究を発展させることのできるものがなく、解析学の新たな展開は17世紀まで待たなければならなかった。もっとも、フランスのオレームNicole Oresme（1330―82）は、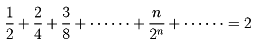

のようないろいろな級数を扱っているし、フランスのビエタF. Vièteは、アルキメデスの与えた円周の長さの計算から、いわゆるビエタの公式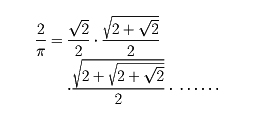

をつくった。

　17世紀初め、ガリレイは、いろいろな図形の重心や慣性モーメントを計算し、またイタリアのカバリエリは、図形が線分や薄板でできていると考えてカバリエリの原理を案出し、図形の面積や体積を求めている。パスカルの求積法も同じような考え方、方法論によっている。17世紀前半には、イギリスのネーピアや、スイスのビュルギによる対数の発見があり、それまでに知られていた三角関数などとともに、関数概念を形成していくうえで大きな影響があった。デカルトによって図形と式を結び付ける解析幾何学が創始されたことは、微分積分学が誕生するうえで決定的な意味をもつものであった。実際、フェルマーやイギリスのバローは、この結び付きをもとに、曲線に接線を引く方法を研究した。ベルギーのサン・バンサンGregorius Saint Vincent（1584―1667）は、双曲線y＝1/xの下の面積が、対数の性質をもつことを発見している。

［竹之内脩］

17世紀後半～18世紀

17世紀後半の1665年にニュートンが、1675年にはライプニッツが微分積分法を発見した。ニュートンのこの発見は、不十分な形で近辺の数学者にのみ伝えられていたようで、ライプニッツはまったく独自に自分の研究を発表したのである。1667年に二度にわたってニュートンからライプニッツにあてた手紙、およびその返書により、お互いの研究が交換された。

　このころは、関数を展開することが大きな関心の対象となった。1665年にニュートンが一般の二項定理を、1668年にメルカトルNicolaus Mercator（1619―1687）がlog(1＋x)の級数展開を、1669年にニュートンがsinx、cosxの級数をみいだしている。ライプニッツの公式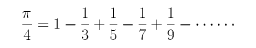

は1676年のニュートンへの手紙の中に登場する。これらの一般形であるテーラーの公式は1715年に発表された。スイスのヤコブ・ベルヌーイとその弟ヨハン・ベルヌーイは、ライプニッツの微分積分法を独自に研究し、発展させた。そして、ニュートン、ライプニッツに始まる微分方程式を研究して、そのいろいろな解法を発見している。

　18世紀に高くそびえるのはオイラーである。『無限小解析入門』（1748）において、系統的な解析学の叙述が初めて展開された。自然対数の底(てい)eの導入、そしてオイラーの公式
　　e^ix＝cosx＋isinx
などが論じられている。さて、ニュートンが微分積分法と同時に確立した力学の原理は、その後の解析学の発展の重要な契機となった。ベルヌーイによって変分法の問題が論ぜられ、また弦の振動の問題が、テーラー、ダランベール、オイラーによって研究されている。また18世紀末、ラグランジュは解析力学を創始した。ラプラスの天体力学も壮大な理論である。

［竹之内脩］

19世紀以後

19世紀は、解析学の足元を見直し、その明確な基礎をつくっていった時代であった。実数の理論が現代的な形をとるのは、19世紀後半、ワイアシュトラース、デーデキント、カントルらの研究のあとのことであるが、コーシーはすでにその『解析教程』（1822）において、いわゆるコーシーの判定条件を明記している。これは実数を公理的に定義するのに十分な命題であった。コーシーはまた積分の定義を明確にしようとしたが果たせず、それはリーマンに帰せられることになる。コーシーはさらに、微分積分法を複素変数の場合にまで進め、複素関数論の基礎をつくった。これは、ワイアシュトラースによって解析関数の理論へと発展した。また、ガウス、ヤコービによる楕円(だえん)関数論も、その後の数学全般に与えた影響は大きい。

　一方フーリエは『熱の解析的理論』（1811）において、関数をフーリエ級数に展開し、あるいはフーリエ積分で表現し、それを活用することを論じた。これは、そのままでは数学的理論になっていなかったが、のちにディリクレらによって基礎づけられ、現在の解析学の重要な手段となっている。下って1870年代、カントルが始めた位相空間の議論は、解析学のなかにも取り入れられた。そして、20世紀初頭のフレドホルムやヒルベルトの積分方程式論は、抽象的に発展してヒルベルト空間の理論となり、量子力学の誕生とともに、物理学にも重要な手段を提供することになった。ヒルベルト空間の理論は、広く発展して関数解析となり、今日の解析学の特徴ある姿をつくっている。

［竹之内脩］

『小堀憲著『数学の歴史5　18世紀の数学』（1979・共立出版）』

[参照項目] | 解析幾何学 | 解析力学 | 関数解析 | 実数

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

解析学 (かいせきがく)
analysis

解析学は，代数学，幾何学と並べられる数学の主要部門の一つである。古く17世紀前半R.デカルトの時代には，記号による算法を漠然と解析と呼んだ。それで17世紀後半にI.ニュートンとG.W.ライプニッツの発見した微分積分法は，無限小の解析とも呼ばれた。現在では，無限に関する極限の概念をおもな対象とする数学の分野を総称して解析学という。

　ニュートンとライプニッツによって発見された微分積分法は，19世紀に入ってA.コーシーによって一応その体系が整えられた。彼の二つの著書（1821，23）においては，当時までの単なる記号演算としての微積分学から脱却して，極限の概念に立脚した解析学の基礎が述べられている。現在の日本の大学初年級における微積分の課程は，大筋においてはほぼコーシーによって組織された形であるといえる。すなわち，変数と関数の定義，連続性，無限級数の収束・発散，導関数と積分の定義，平均値の定理などが述べられている。それらは今日の観点からは部分的には不十分な個所も多いが，当時までの不完全さと比べて著しい厳密さで展開されている。

　19世紀の中ごろになって，微積分学は一方ではコーシー，G.リーマン，K.ワイヤーシュトラスらによって，複素変数の関数を研究対象とする解析関数論の方向に一般化されて発展し，他方では解析学の基礎的な諸概念を確立し精密にするという方向に発展することにより，実変数関数論の分野ができた。前者の分野は複素関数論，または単に関数論と呼ばれ，後者は実関数論と呼ばれる。実関数論の方向は，J.フーリエの熱伝導に関する有名な論文（1812）に現れたいわゆるフーリエ級数に端を発するといえる。すなわち，P.ディリクレはフーリエ級数に関する二つの論文（1829，37）において，関数の現代的な定義を確立したが，その後リーマンが積分の一般的な定義を確立（1854）し，G.カントルが無理数論および集合論を創始した（1872）のも，フーリエ級数が誘因の一つであったと思われる。さらに20世紀の初めに，H.ルベーグは彼の名を冠した測度の概念を導入し，それをもとにしたルベーグ積分の理論を創始した。実関数論はルベーグ積分論を核として発展し，フーリエ級数やフーリエ解析における多くの著しい結果が得られているが，ルベーグ積分論は，後に述べる関数解析学においても基本的な役割を演じ，欠くことのできない理論である。

　未知数を含む通常の方程式に対し，未知関数の導関数を含む方程式を微分方程式という。ニュートンの運動方程式は2階の微分方程式で表され，したがって，万有引力の法則による惑星の運動も2階の微分方程式で表される。このように自然の法則は微分方程式によって記述されるものが多いので，微分方程式論は微積分学と同時に創始された。ニュートンはそれらの微分方程式を解き，また18世紀前半には特殊な方程式を個々の方法で解くこと（求積法）に重点がおかれたが，18世紀の後半には無限級数による解法が研究された。さらにコーシーが解の存在問題を研究（1820）して以来，理論的研究が発展した。

　未知関数の偏導関数を含む方程式，すなわち偏微分方程式は，J.ダランベール，L.オイラーが流体力学に関する物理的問題の取扱いで初めて研究し，解の存在定理はS.コワレフスカヤにより発表された（1875）。物理的な問題との関連から，2階線形偏微分方程式の境界値問題，初期値問題が19世紀まで主として研究され，20世紀に入ってからは，関数解析学の手法を応用することによって，粘性流体の研究に現れる非線形問題や，量子力学におけるシュレーディンガー方程式の研究が発展した。

　N.アーベルは重力場で落下する質点の軌道の形と落下時間の関係を論じた（1823）。落下時間と軌道の始点・終点を与え，軌道を表す関数を未知関数とすると，これを求める問題は未知関数やその合成関数の積分を含む方程式で表される。このような方程式を積分方程式という。また，軌道の両端点を与えて落下時間を最小にする問題のように，指定された境界条件を満たす関数の中で，それに対応する実数値を最小にするものを求めることを変分法という。積分方程式や変分法は，19世紀以来，個々の型の問題に対する解法が盛んに研究されたが，20世紀に入ってそれぞれ統一した理論が築かれ，とくに積分方程式論は完全に関数解析学の研究対象となった。

　20世紀に入ってから創始された関数解析学の特徴は，個々の関数を研究対象とするのではなくて，ある条件を満たす関数の集合を一つの空間（関数空間）と考え，その空間の中でベクトル算法や収束の概念を扱うのである。その際，微分，積分などの演算は関数空間の点から関数空間の点への写像と考えられ，一般に作用素と呼ばれる。関数解析学においては，作用素がおもな研究対象であるが，一般論を展開するにも，具体的に取り扱われる多くの有用な関数空間の構成にもルベーグ積分が使われる。ルベーグ積分では種々の極限操作が非常に簡便な条件のもとで行われるので，それを使って構成される関数空間が完備な距離空間になることは，その有用性の典型的な例である。関数解析学の最初の成果は，積分方程式に関するフレドホルムの定理の抽象化を含むD.ヒルベルトの論文集（1912）であり，続いてS.バナッハはその著《線形作用素論》（1932）においてこの分野の基礎を築き上げた。現在もなお重要な研究対象であるヒルベルト空間，バナッハ空間の名は，この2人のパイオニア的業績による。さらに，20世紀の中ごろにL.シュワルツによって創始された超関数の理論により，偏微分方程式への応用も著しく進展した。

　以上のように，微積分学をはじめ，それに続く微分方程式，積分方程式，変分法，実関数論，複素変数の関数論，関数解析学など，解析学の包括する分野はたいへんに広い。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

解析学【かいせきがく】

極限の概念を主対象とする数学の部門の総称。微分積分学をはじめとし，それから発展した関数論，微分方程式論，積分方程式論，変分法（変分学），関数解析など広範囲にわたる。→解析／解析幾何学
→関連項目位相数学｜コーシー｜実変数関数論｜ラプラス

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

解析学
かいせきがく
analysis

関数についての理論を，連続変数に関する連続性・微分可能性などを中心に研究する数学の一分科をいう。微分積分学，微分方程式論，積分方程式論，変分学，測度論，級数論，フーリエ解析，ベクトル解析，実変数関数論，複素変数関数論，ポテンシャル論などと，これに続く諸分科がこれに含まれる。

出典　ブリタニカ国際大百科事典 小項目事典