日本大百科全書(ニッポニカ) 「微分積分法」の意味・わかりやすい解説
微分積分法
びぶんせきぶんほう
differential and integral calculus
微分積分学、または微積分法、微積分学ともいう。微分法と積分法とをあわせた名称であるが、それぞれの数学的内容については「微分法」「積分法」の項目に譲り、ここでは、主として、その歴史的な側面について述べる。
［竹之内脩］
ニュートン、ライプニッツによる微分積分法の創始
イギリスのニュートンは、f(x,y)をx、yの多項式としてf(x,y)=0という曲線上を動く点を考えた。そして、この点の水平方向の速さ、垂直方向の速さをそれぞれ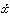
、
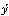で表し、これらをx、yの流率とよんだ。この流率の比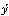/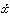は接線の傾きであり、あるいはyのxに関する微分係数であるが、これを求める方法、すなわち微分の方法を考えた。次に、この逆演算、すなわち、与えられた流率の比となるようなもとの関数f(x,y)=0を求める方法を考察した。こうして図形の面積を求める問題は、この演算、すなわち積分法に帰着されることを示し、これによって、それまで個々ばらばらのやり方で扱われてきた図形の求積は、積分法として統一的に取り扱われることとなった。微分積分法の基本定理は、のちにこれらの考え方を整理して定理化されていったものである。ニュートンは微分の方法としては、合成関数の微分法まで考究している。
彼は、これらの内容を1666年に論文にまとめたが、それはその後の30年間出版されることはなく、ニュートンの生存中にこのことを知っていたのは、ほんのわずかのイギリスの数学者のみであった。次に述べる「無限級数の方程式による解析について」の論文も、ニュートンは1669年にまとめていたが出版されたのは1711年で、それまでは、そのことを知る人間はほとんどいなかった。すでにメルカトルは、y=1/(1+x)の下の、x座標が0からxまでである部分の面積として、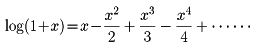
を与えていた（1668）。ニュートンは、これに刺激されて前記の論文を書いたが、このなかで、まず方程式の解を求めるニュートン法（ニュートン‐ラフソン法）を提示した。そして、その方法を延長してlog(1+x)=zを解いて、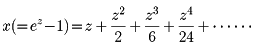
を得た。さらにこの方法を、級数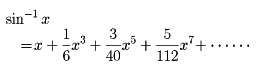
に適用して（θ=sin-1xとする）、ついに、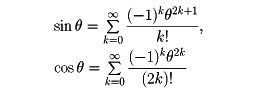
であることを導き出している。
1671年にニュートンは、それまでに得た結果を出版しようとしたが、これも果たさず、それは彼の死後の1736年にやっと日の目をみることになった。これには極大・極小問題、曲線の弧の長さ、置換積分法などが扱われ、不定積分の表も載せられている。彼は1676年、ドイツの数学者・哲学者ライプニッツに手紙を送り、自分の到達した結果を述べて、自分の発見の優先性を主張している。その後、彼は『プリンキピア』（『自然哲学の数学的原理』）を著し、また晩年には求積法の著書を著し、それまでの諸結果をまとめた。そのなかでは級数展開の方法をしばしば利用している。
ライプニッツが微分積分法の理論の発見をしたのは1672～1676年のことである。この間の業績は多数の手記として残されている。ライプニッツは、曲線上の1点でつくった微小三角形（特性三角形とよぶ）を利用して、曲線で囲まれた図形全体の面積を求める方法を考えた。その際、微小部分の面積の和という意味で、積分記号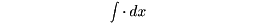
を考案している。また彼は、部分積分法の公式を得て、これを活用してもいる。さらに、特性三角形における辺の比の考察から、合成関数の微分法にも到達している。のちにライプニッツは、高次微分の概念をつくり、曲率の公式も得ている。
同時代にあって、ニュートン、ライプニッツの微分積分法の発見は独立になされたが、2人のうちどちらの発見が早かったのか、あるいは、どちらかは他の発見に負うているのではないかということをめぐって、イギリスと大陸の間で海を挟んで論争が起こっている。イギリスでは、ニュートンの発見の枠にとどまったままで、その後それを数学理論として大きく発展させることができなかったのに対し、大陸のほうでは、ライプニッツの発見の後を受けて、解析学の方法を大きく発展させることとなった。
ニュートンは、まず個別の問題の究明を手がけ、それをさらに一般化・普遍化していくという方法論をとったのに対し、ライプニッツは、まず普遍妥当な一般的原理に着目し、それが個別の問題に適用できるかどうか考察するという方法をとっている。また、ニュートンにおいては、流率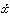,,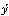……が基本の概念となっているが、ライプニッツにおいては、無限小dx,dy,……が中心の概念となっている。さらに、ニュートンは、数学記号には無頓着(むとんちゃく)であったが、ライプニッツは、記号の神様といわれるように、微分積分法のいろいろな記号を案出し、それが広く用いられることとなった。
［竹之内脩］
微分積分法のその後の発展
ライプニッツの仕事は、ヤコブ・ベルヌーイ、ヨハン・ベルヌーイの2人に受け継がれた。ヨハンのほぼ同年の友人および庇護(ひご)者であるロピタル侯爵が1696年に著した『曲線を理解するための無限小解析』は微分法の最初の教科書ともいえる。このなかには、よく知られているロピタルの定理が述べられている。
その後の微分積分法の発展に貢献したのはオイラーである。オイラーは『無限の解析学入門』Introductio in analysin infinitorum（1748）のなかで、指数関数、対数関数の性質を基礎づけている。まず、εを無限小の数として、aε=1+kεと考え、与えられたxについてx=Nεと置いて、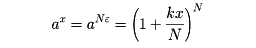
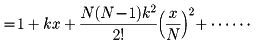
とし、これから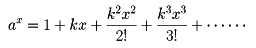
を導いた。とくにk=1の場合になるaとして自然対数の底eを導入した。今日の記号では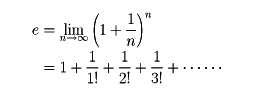
である。また、1+y=axとすれば、オイラーの記法で1+y=aNε=(1+kε)Nしたがって、1+kε=(1+y)1/Nゆえに、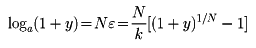
である。これは、今日の記号では、a=e,k=1のとき、yをxと書き換えて、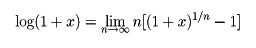
である。これに二項展開を適用して、メルカトルの得た展開式を導く。今日の時点でみれば、これらは厳密さを欠く論法ではあるが、歴史的にみれば興味深い。
また三角関数についてのド・モアブルの公式
(cosz±isinz)n=cosnz±isinnzから、前と同様の無限小の利用により、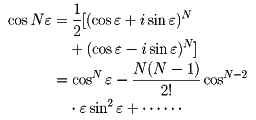
ここで、cosε=1,sinε=ε,N=N-1=N-2=……として、ニュートンと同様のcosx,sinxの展開式を得ている。また、これから、オイラーの公式
eix=cosx+isinx
を導いている。オイラーは、このほかにも、微分法・積分法に関して大きく貢献した。
ニュートンの方法は、イギリスの数学者テーラーに受け継がれた。テーラーは1715年に著した書物で、流率法の効用を強調すると同時に、テーラーの展開を示した。テーラーのこの定理は、18世紀末のラグランジュの『解析関数論』Théorie des fonctions analytiques（1797）あたりから、さらに精密化されていくことになる。ラグランジュは、不完全な形であるが、平均値の定理を与えている。これは、微分積分法についてのもっとも根本に位置する定理であるが、その後だんだんと今日の形に整えられていった。
19世紀に入ると、1821年にコーシーが『解析学講義』Cours d'analyse de l'Ecole Polytechniqueを著し、ここで、今日の微分積分法の方法論は完全に整備された。彼は極限概念を中心に据え、それと論理的に整合した形の微分積分法を築こうとしたのである。その後も、多くの数学者により、さらにさまざまな点が補われて、今日の微分積分法の体系ができあがっていった。
［竹之内脩］
『P・ラックス著、竹之内脩監修『解析学概論』（1982・現代数学社）』▽『一松信著『解析学序説』（1982・裳華房）』▽『高木貞治著『解析概論』（1983・岩波書店）』▽『石原繁・浅野重初著『微分積分 理工系の基礎 増補版』（1997・裳華房）』▽『俣野博著『現代解析学への誘い』（2004・岩波書店）』