日本大百科全書(ニッポニカ) 「数学史」の意味・わかりやすい解説
数学史
すうがくし
数学は、物を数えたり、測ったりすることに始まる数・量に関する学問であり、数や量に潜む微妙な関係を追究する数学研究は人間の精神の豊かさを示してきた。また、研究によってより豊かにされた数学は、自然現象の解明に、基本的な方法と強力な手段を提供してきた。数学の発展の流れを概観してみよう。
［小堀 憲］
数えること
数学の起源はきわめて古いが、文字のなかった有史以前のことは、考古学的資料によるほかはなく、「仮説」の域を出ない。
文字のなかった時代でも、部族の人数を数えたり、獲物の頭数を調べたであろう。つまり「数える」ことは人間の出現とともに始まった、といってよい。この「数える」ことが基本となって、「数」が形成されたであろう。しかし、その経緯は明らかでない。この時代の人間は、食物を求めて放浪する生活であったであろうから、地積を求める必要はなく、したがって、「幾何学」の前身といえるものは生まれなかった。文字ができて記録が残されるようになったとき、そうした有史以前の状態からどのようにして発展したか、その過程をたどることができないほど進んだ数学が形成されていた。
［小堀 憲］
最初の数学
ティグリス川とユーフラテス川とは下流で一つになってペルシア湾に注ぐが、この二つの川の流域を中心とする古代メソポタミアに、紀元前50世紀にシュメール人の文化が形成され、その後カルデア人によってバビロニア帝国が建設されたときには、文化は輝かしいものになっていた。ここでは「楔形(くさびがた)文字」が発明され、粘土板に刻まれ、記録が残された。数字も楔形文字で、数を示すのに十進法と六十進法とが併用された。数学の問題は、現代の数学ならば二次方程式へ導いたであろうと思われる程度のものである。
同じころに、ナイル川の流域で発達した古代エジプトの数学がある。エジプトでは「象形文字」を使ったが、数字も同様であり、十進法を用いた。数学に属する記録は「リンド・パピルス」（大英博物館）と「モスクワ・パピルス」（プーシキン美術館）の二つに残されており、前者には「数」に関するものが多く、後者には「図形」に関するものが多い。いずれも程度は高いが、結果だけが示されており、その結果に到達する過程は全然述べられていない。
［小堀 憲］
古代ギリシア――純粋数学の誕生
メソポタミアやエジプトで発達した数学を学問としての数学に発展させたのは古代ギリシアであった。それを最初に行ったのはミレトスで生まれたタレスで、彼は商人である。メソポタミアやエジプトを商用で旅行し、この地域で発達した数学に魅せられ、研究に専念するようになった。しかし彼は、メソポタミアやエジプトの数学をそのまま継承したのではなく、さまざまな数学の問題を、普遍性をもつように、抽象化して証明し、応用も示した。タレスに次ぐ数学者はサモス出身のピタゴラスである。彼はメソポタミアやエジプトで数学を学んだが、故郷がペルシア軍に蹂躙(じゅうりん)され、その支配下に置かれて、自由を奪われていたので、南イタリアのクロトンへ逃避し、ここでピタゴラス学派を形成した。この学派では「一つの線分は有限個の点で構成されている」と考えていたが、この仮定が誤謬(ごびゅう)であることに逢着(ほうちゃく)し、「有限個でないもの」と「無理数」（有理数でない数）とが存在することを発見して驚愕(きょうがく)した。
前5世紀からギリシア本土のアテネは文化の中心となったが、哲学者プラトンはアカデメイアという名の学校を創設し、数学を基調とする教育を行った。同じころにクニドスではエウドクソスも数学に精進していた。前323年にアレクサンドロス大王が急死し、その広大な領土は部下によって分割統治された。エジプトを領有したプトレマイオス1世はナイル川下流のデルタ地帯のアレクサンドリアを首都に選び、ここに研究機関ムセイオンを建て、図書館を付置するなど研究環境を整えて、多くの学者を集めた。そのなかの1人ユークリッド（エウクレイデス）は、過去の数学を体系づけて13巻からなる『ストイケイア』をまとめた。「ストイケイア」とは「粋」という意味のギリシア語であって、英語では「elements」と訳し、日本では「原論」と訳している。この書物は内容も重要であるが、その形式がより重要である。これによって、純粋に論理的に探究する「科学」としての数学が誕生したのである。その後アルキメデスは、数学に計量的な要素を取り入れ、数学の応用分野として力学を開拓し、アポロニオスは「円錐(えんすい)曲線」に関する著書を公にしたが、この2人を最後に、ギリシアの数学は衰退し始めた。プトレマイオスは『メガレ・シュンタクシス』（大集成）という名の書物を、パッポスは『シュナゴーゲ』（論文集）を、ディオファントスは『アリツメティカ』（数論）を公刊して最後の気を吐いた。しかし、ローマの軍隊がアレクサンドリアに侵入したとき、この首都は焼き払われ、ギリシアの文化財も焼失した。プトレマイオスの『大集成』も例外ではなかったが、幸いにもアラビア語訳『アルマゲスト』が残っていた。後世ではこの書名のほうがよく知られ、原名は忘れられてしまった。ディオファントスの『数論』も17世紀になってヨーロッパに知られるようになった。これも、メズィリアクBachet de Méziriac（1581―1638）のラテン語訳によってである。
［小堀 憲］
中世――2冊の数学書
そのころヨーロッパには優れた数学者はいなかった。5世紀末にボエティウスは『数論の原理』Institutis arithmeticaeを公刊したが独創的なものではなかった。これに対してアラビアでは数学は発達していた。9世紀には数学者アル・フワーリズミーが代数学書『Kitab al-gebr w'al-mukabala』（移項と整頓(せいとん)の書）を公刊した。これは二次方程式の解法を示したものであって、現代の数学で「二次方程式の解の公式」と称しているものはこの書物に出ている。この時代にはまだ式がなかったので、ことばで示されている。この方法がヨーロッパに広がったのは、1202年ピサのレオナルド（フィボナッチ）が、アル・フワーリズミーの著書をまねて、ラテン語の『Algebra et Almukabala』を書名とする著書を公刊してからである。この書物はヨーロッパで広く読まれたが、本文がLiber abaciということばで始まっているので、本来の書名よりも『Liber abaci』（計算の書）という名のほうが著名である。ちなみに、方程式の解法を取り扱う数学をalgebraと名づけるようになったのは、この書名に由来する。
［小堀 憲］
インド・中国の数学
インドの数学の起源は古く、商業上の必要から発達したので、計算が重要な役割を果たしていた。現代の「算用数字」は「アラビア数字」とよばれるが、本来、インドで創案された数字から派生したものである。また5世紀ごろには数としての「零」が導入された。これに関する性質をブラフマーグプタがその著書（628）において示しているが、さらにブハースカラが1150年に公刊した『リーラーバーティー』において、零の計算についての演算規則を示している。しかしこれらのことをヨーロッパに伝えたのは、これらをアラビア語に訳したアラビア人、というよりも、このアラビア語のインド数学をラテン語に訳したヨーロッパ人である。したがって、インドの数学は、直接には、後世の数学の発展には影響しなかった。
中国の数学も歴史は古いが、ヨーロッパの数学への影響はなかった。この恩恵を受けたのは日本である。
中国でもっとも古い数学書は、『周髀算経(しゅうひさんけい)』であるといわれている。紀元前100年ごろのもので、測量が中心となっている。このなかに「勾股弦の理(こうこげんのり)」があるが、これは「ピタゴラスの定理」と同じものである。その後に、後漢(ごかん)の時代になって『九章算術』が世に出た。これらとこの時代に出た『海島算経』『孫子算経』などが6世紀の中ごろに、朝鮮半島を経由して日本に渡来したが、これらは庶民の手には届かなかったようである。1299年に朱世傑(しゅせいけつ)は『算学啓蒙(けいもう)』を著し、「算籌(さんちゅう)」（算木）を用いて数を表し、それを演算（加減乗除および開平、開立）する方法を説明し、「天元術」（問題を未知数が一つの代数方程式へ転換して解くという方法）を樹立し解説している。1592年に程大位(ていだいい)が著した『算法統宗』は、「そろばん」を用いて数を表し、それを用いて演算することを示している。これらの書物は、17世紀の初期に日本に渡来、広く一般の人に行き渡り、やがて「和算」を形成して一時期を画した。しかし、中国、日本とも、論理的建設に欠けていたため、ヨーロッパ数学の到来とともに没落していった。
［小堀 憲］
16、17世紀――創造的な時代
15世紀に印刷術が発明されて以来、科学書の出版が盛んになり、研究熱も高まった。イタリアのフォンタナ（タルターリア）は三次方程式の一般的な解法を樹立した。彼はこの方法をカルダーノに教えたが、カルダーノは1545年に公刊した書物『偉大なる方法』Artis magnaeのなかでこれを公表したため、現代の数学では「カルダーノの公式」とよんでいる。さらにこの書物にはカルダーノの門人フェッラーリLodovico Ferrari（1522―1565）が樹立した四次方程式の解法が示されているが、まだ「式」のなかった時代であり、これらの「公式」も「ことば」で述べられていた。
16世紀末にフランスのビエトは、数学に文字や演算記号を導入し、これが17世紀の数学者によって改良され、現代の方程式へと発展した。これを用いると二次、三次および四次の方程式の解は、与えられた方程式の係数に、加法、減法、乗法、除法および開法を有限回行って得られる式で示されていることがわかる。方程式の解をこのような式で表すことを、方程式を「代数的に」解く、というようになったが、この解法は19世紀に問題となった。
ユークリッドの幾何学の方法に新しい異種の方法を加えたのはフランスのデカルトである。彼は著書『方法序説』に試論として添えた「幾何学」La géométrieにおいて、「……まず第一に、問題は解けたと仮定し、これを解くのに必要と思われるものに記号をつけ、求める未知のものにも記号をつける……」と書いている。古代ギリシアの数学者は「問題が解けたものと考え、何を明らかにすればよいか、とその問題を解くのに必要な要素をみつける」ことを目ざした方法を「解析」と名づけていたので、デカルトの幾何学を「解析幾何学」とよんでいる。この幾何学では、図形に関する問題を解くことを、方程式を解くことへ転化した。方程式を取り扱うとは、「想像」に頼ったり、「偶然」を頼みにしたりする必要がなくなったことであり、したがって、幾何学は「悟性」だけに基づいて、方法論的に処理することができるようになった。
同じころに、フェルマーは、バシェClaude-Gaspar Bachet de Méziriac（1581―1638）が翻訳したディオファントスの『数論』を研究し、「与えられた平方数を二つの平方数の和に等しくなるように分けること」という問題を拡張して、「立方数を二つの立方数の和に、四乗数を二つの四乗数の和に、さらに一般に、2よりも大きな冪(べき)の数を、同冪の二つの数の和に分けることは不可能である」と述べ、「私は実に特異な証明をしたが、余白が狭いので書くことはできない」と付け加えている。フェルマーは読んだ書物の欄外に自己の考えたことを書き添えていたから「余白が狭い」と書いたのであるが、この問題は現代に至るも証明されず、「フェルマーの最後の定理」の名で伝えられている。この時代のパスカルは16歳のときに『円錐曲線試論』を公表しているが、これは「射影幾何学」の誕生につながる業績である。また、「賭(か)け金の分配」に関連して交換されたパスカルとフェルマーとの間の往復文書は、確率論形成史に重要な役割を演じている。
パスカルにすこし遅れて、イギリスにニュートンが現れた。彼は運動している量を「流数」と名づけ、それの速度を「流率」とよび、運動の問題を離れて流率を求める問題を独立して考えた。流数をxで表したとき、xの流率を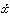
で示し、逆に流率がxであるときの流数を［x］で示して、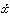や［x］を求める演算法を「流率法」と命名した。この新しい演算法の導入によって、力学や数学に著しい影響を及ぼしたのである。同じころ、ドイツではライプニッツが、一つの曲線の接線を求めることに関連して、「微分」と名づけた量を導入し、二つの微分の商を「微分商」とよんで、微分の演算規則を設け、「微分法」を樹立した。また、ニュートンが［x］で示したものをxの「積分」と名づけて、これを求める演算法を「積分法」と名づけた。ニュートンとライプニッツとは同じ演算法を発明したのであるが、ライプニッツの記号のほうが優れていたために、ヨーロッパ大陸ではライプニッツの記号が広く用いられるようになった。
［小堀 憲］
18世紀――自然科学への応用
17世紀が創造的な時代であったのに対して、18世紀には、新しい数学は一つも生まれなかった。しかし、この世紀の数学者が手がけた論文や著書をみると、それらを踏み台として19世紀の数学が生まれたことは明らかであり、新しい数学の誕生において、18世紀は見逃してはならない時期であったというべきであろう。
イギリスでは、B・テーラーとマクローリンとが、ニュートンの流率法を応用して、関数を冪級数で表すことを創案した。これは、19世紀への大きな遺産となった。スイスでは、ジャック（ヤコブ）とジャン（ヨハン）のベルヌーイ兄弟およびオイラーがライプニッツの微分積分法とそれの応用とを発展させた。とくにオイラーは800ページに及ぶ『無限の解析学入門』Introductio in analysin infinitorum（1748）において、初めて「関数」の定義を与えた。この定義によると、「関数すなわち式」となり、現代の数学からみれば素朴なものであるが、「定義した」ことは、その後の数学に重要な影響を及ぼした。そのほかオイラーの研究は数学の広い分野にまたがり、数多くの業績を公表した。彼の研究は厳密性に欠けるところがあったが、大胆な論法であった。フランスでは、ジャン・ベルヌーイの門人ロピタル侯François Antoine de L'Hospital（1661―1704）が、その著書においてライプニッツの記号が優れたものであることを示し、ライプニッツの微分積分法の価値を高めた。また、ダランベールは、弦の振動という物理現象の解明を、偏微分方程式を解くことへ転換したが、このときに「一般の関数とは何のことであるか」という新しい問題を提起し、クレローは天体力学と解析学とにおいてその名を残している。
1787年にルイ16世はフランス系イタリア人のラグランジュをパリへ招いた。彼は着任の翌年に画期的な『解析力学』Mécanique analytiqueを公刊した。1789年7月14日、フランスで大革命が勃発(ぼっぱつ)し、政治面だけではなく、あらゆる方面に大きな変革がもたらされた。学問が庶民に開放されたこともその一つである。それまでは貴族に独占されていた高等教育も庶民に開放された。革命政府は英才教育の機関としてエコール・ポリテクニク（理工科大学校）とエコール・ノルマル・シュペリュール（高等師範学校）を設置した。エコール・ポリテクニクでのラグランジュの講義の原稿ともいうべきものが、この学校の紀要にあるが、それが『解析関数論』Théorie des fonctions analytiquesで、これが19世紀の数学者に大きな影響を与えた。ラプラスもこの時代にパリにいて、天体力学、数理物理学および確率論において活躍した。ことに、1812年に公刊した『確率の解析的理論』Théorie analytique des probabilitésは20世紀に至るも高い評価を得ていた。さらに、エコール・ポリテクニクの教授であり校長であったモンジュは「画法幾何学」を樹立し、また、偏微分方程式の解法に微分幾何学を応用して新しい方法を樹立した。ルジャンドルも、解析学、整数論に輝かしい成果をあげた。とくに「楕円(だえん)積分」に関する研究は、19世紀の数学者に、新しく、「楕円関数論」を樹立する動機を与えたものである。
18世紀の数学者の論文や著書には、著者の精神の「たくましさ」があふれている。このたくましい数学者たちによって導入された荒削りの数学を、根底から築き上げて、新しい数学をつくったのが19世紀の数学者たちである。
［小堀 憲］
19世紀
1822年にフランスのフーリエが公刊した大著『熱の解析的理論』Théorie analytique de la chaleurは、「熱の伝導」という物理現象の研究を偏微分方程式の解の研究へ転化したものであるが、数学からみてとくに重要なのは、「すべての関数を三角級数で表すことができる」と予想したことである。
フランスのコーシーは微分法と積分法とを根底から検討して、あいまいな概念を明確にし、「微分積分法」を「解析学」の一分科へと高めた。さらに、複素数を変数とする関数の微分法と積分法とを定義して、一連の基本定理を樹立した。ついで、ドイツのリーマンとワイアシュトラースとが飛躍的な発展をさせ、「関数論」を樹立し、のちには「ワイアシュトラース流」「リーマン流」とよばれるようになった。先に述べたフーリエの予想に取り組んだのは、ドイツのディリクレで、一つの関数が三角級数で表すことができるための条件（ディリクレの条件）を設けた。これを検討したリーマンは、コーシーの樹立した積分定理ではディリクレの条件を満たさないことを明らかにし、現代の数学で「リーマン積分」と称しているものを樹立した。解決には至らなかったが、リーマンの仕事に刺激されたのはドイツ人G・カントルである。彼は「集合」という概念を導入して、この問題に挑戦し、飛躍的に発展させたが、結果はフーリエの予想とはほど遠いものであった。フーリエの予想は「フーリエ級数論」の名で20世紀の数学者に託された。
1799年に「すべての代数方程式は解をもつ」ことを証明した論文をひっさげて数学界に登場したガウスは、数学のあらゆる分野ですばらしい業績を残した。なかでも、整数論、曲面論および誤差論における研究は、その後の数学界に大きな影響を与えた。とくに1801年に公刊された『数論の諸研究』Disquisitiones arithmeticaeは、数学史における金字塔である。
この時代にハンガリーのJ・ボヤイは「平行線」に関するユークリッドの公理、すなわち「直線外の1点を通って、その直線に平行な直線は、一つあってただ一つに限る」だけを否定する幾何学を樹立した。同じころ、ロシアのロバチェフスキーも同じ幾何学を樹立した。この幾何学はユークリッドの「平行線の公理」を否定した公理に基づいて樹立されたため、後世ではこれを「非ユークリッド幾何学」とよぶ。
公理群のいくつかを他の公理で置き換えて「新しい幾何学」を創造するという思想は、ポアンカレ、リー、ヒルベルト、クラインに影響を与え、なかでもヒルベルトの『幾何学基礎論』Grundlagen der Geometrie（1899）、クラインの『エルランゲン目録』（1872）が指針となり、20世紀の幾何学が生まれた。幾何学だけではなく、数学のあらゆる分野で、「公理的建設」と「群論的建設」の機運が生まれたのである。
16世紀の数学者が、三次および四次の代数方程式が代数的に解けることを具体的に示して以来、五次方程式について、17～18世紀の数学者がこの問題に挑んだが、成功した者はなかった。19世紀になって、ノルウェーのアーベルとフランスのガロアの2人が、それぞれ独立に「群」の概念を導入して、「五次以上の代数方程式は、一般には、代数的に解くことはできない」ことを証明した。この2人はいずれも20歳代で他界し、その業績は死後に認められ、称賛された。
［小堀 憲］
現代
前記のように、19世紀には輝かしい数学が完成され、さらに新しい道が開かれた。20世紀に入ってからは、数学はいろいろな分野へ分岐し、20世紀後半に入ったころには、「集合論」「群論」「抽象代数学」「関数論」「関数解析学」「微分方程式論」へと分化した。歴史の古い幾何学だけを取り上げても、「射影幾何学」「微分幾何学」「射影微分幾何学」「広域微分幾何学」「積分幾何学」などに分かれて、1人の幾何学者ではそのすべてを把握することはできない、といっても過言でないほどになっていた。
数学と他の科学との関係は古い。物理学との関係はアルキメデスに始まるが、ニュートンに至っては、物理学が新しい数学をつくりだし、それによって物理学は飛躍した。このときから、数学は物理学によって新しい道を開拓するようになった。20世紀初頭にアインシュタインは四次元幾何学の力を借りて、特殊相対性理論を樹立、さらにリーマン幾何学の導入とテンソルの利用によって、これを「一般相対性理論」へと拡張した（1916）。またイギリスの物理学者ディラックが量子力学の研究において導入したデルタ関数が引き金となって、フランスのシュワルツは「超関数」の理論を樹立して、「微分法」の概念を拡張した。
このような発展の原動力となったのは、20世紀の前期に出版された『ケンブリッジ全書』Cambridge tracts、『ボレル叢書(そうしょ)』Collections Borel、『科学ノート』Cahiers scientifiquesおよび『数学の成果』Ergebnisse der Mathematikの出版である。なお、カントルの集合論が出現して以来、数学における概念の形成について反省し検討を加えようとする機運が生まれた。オランダのブローエルLuitzen Egbertus Jan Brouwer（1881―1966）は、数学の論理的基礎にも一種の直観が潜んでいる、という直観主義の立場で数学をとらえた。これに対してドイツのヒルベルトは、数学は公理群から命題を純粋に形式論理的に演繹(えんえき)することだけで組み立てられると考えて、直観主義と対立した形式主義をとっていた。
他方、イギリスのB・ラッセルは、数学は論理学の一分科である、という立場を研究の基礎とした。そして記号論理学を手段として研究し、その成果をホワイトヘッドと共同で『数学原理』Principia Mathematica（1910～1913）に集大成した。このような方法で数学を研究することを「数学基礎論」という。
国際数学者会議が4年ごとに開催されるようになったことも見逃してはならないであろう。第1回会議（1897）はチューリヒで開催され、続いてパリで開かれた第2回会議（1900）でヒルベルトは講演し、23個の「問題」を提示して数学界に旋風を巻き起こした。この問題のうち1958年までに解決されたのは11問だけである。1932年の国際数学者会議で「フィールズ賞」が設置され、1936年の国際数学者会議で、フィンランドのアールフォルスが最初の受賞者となった。
一方、数学者でさえもとまどうほどに分化した数学を一つの原理で統一しようとする企てがおこったが、まだ成功していない。たとえば、ブルバキという仮名の集団を組織しているフランスの若い数学者の一群は、多様体という概念を基礎として、数学の全体を立て直すことを企て、1935年以来「集合論」「代数学」「一般位相学」「実関数論」「線形位相空間論」「積分論」を書き上げ、最終的には『数学原論』Éléments de mathématiqueという名でまとめあげるとして、いまなお進行中である。
また、ノイマンは高速度計算機を発明し、その後、電子工学の発展によって性能が高められ、人間頭脳の代用を目ざして、コンピュータという名で発展の途上にある。
［小堀 憲］
『彌永昌吉著『現代数学の基礎概念』（1944・弘文堂）』▽『小堀憲著『大数学者』（1968・新潮社）』▽『カジョリ著、石井省吾訳『数学史』（1970・津軽書房）』▽『高木貞治著『近世数学史談』（1970・共立出版）』▽『近藤洋逸著『数学の誕生』（1977・現代数学社）』▽『伊東俊太郎他編『数学の歴史』全10巻（1979～ ・共立出版）』▽『小堀憲著『物語数学史』（1984・新潮社）』▽『ブルバキ著、村田全・清水達雄訳『数学史』（1984・東京図書）』