汎関数（読み）はんかんすう（英語表記）functional

精選版 日本国語大辞典

はん‐かんすう ‥クヮンスウ【汎関数】

〘名〙 数学で、写像の一つ。定義域が関数から成り、値域が数から成るような写像のこと。

出典　精選版 日本国語大辞典

デジタル大辞泉

はん‐かんすう〔‐クワンスウ〕【汎関数】

関数を変数とし、実数または複素数の値をとる関数。例えば、「x=1からx=2までの区間で、関数y=f(x)が表すグラフの長さ」などがこれにあたる。

出典　小学館

改訂新版　世界大百科事典

汎関数 (はんかんすう)
functional

ふつうの関数は，その変数も関数の値も実数であるから，ある範囲のおのおのの実数に実数値を対応させるものである。これに対し，ある範囲のおのおのの関数に実数値（または複素数値）を対応させる規則があるとき，これを汎関数という。すなわち汎関数とは，一つの関数空間を定義域とし，実数または複素数の値をとる関数である。例えば，区間a≦x≦bで定義されたなめらかな関数y＝f（x）の全体Dを考える。そのような関数は一つの曲線を表し，その曲線の長さは積分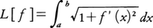，で与えられる。このLはDに属するおのおのの関数fに実数L［f］を対応させているから一つの汎関数である。また，区間a≦x≦bの上の連続関数の全体をCとするとき，この区間で積分可能な一つの関数φを与えると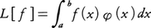，はCの上の汎関数である。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

汎関数
はんかんすう
functional

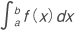定義域が関数空間 {u} に含まれるような実数 (または複素数) 値関数のことで，J[u] などで表わす。普通の関数 y＝f(x)(a≦x≦b) は，1つの実数値 x に対して，1つの実数値 y を対応させる。しかし，たとえば f の定積分 は，1つの積分可能な関数 f に対して1つの実数 I[f] を対応させる。このように関数が定まるごとに1つの実数が定まるとき，これを関数の拡張と考えて汎関数と呼ぶ。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の汎関数の言及

【アダマール】より

…微分方程式論の位相的研究でも美しい結果を得た。汎（はん）関数という言葉を導入し，関数解析学の先駆者となり，流体力学，波動論など数理物理学の分野でも多くの業績を残している。数学教育にも関心をもち，1900年ごろに著した初等幾何学の本は長くリセの生徒に愛読された。…

【関数】より

…
［関数と写像］
　現代数学における用語としては，関数と写像とはまったく同義語であるが，歴史的習慣により，値域が実数または複素数の集合である場合には関数と呼ぶことが多い。定義域が関数の集合であって，値域が実数または複素数の集合である場合には，汎（はん）関数と呼ぶことがあるが，これも歴史的理由による。これらの名称は，その内容を直観的にわかりやすくしていて便利なので，現代でもふつうに使われている。…

【関数解析学】より

…線形作用素Tが連続，すなわち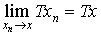，を満たすこととTが有界なこととは同等である。前に述べた作用素の定義で，とくにYが複素数体のとき，その作用素のことを汎関数という。
［共役空間，共役作用素］
　Xの上の有界線形汎関数fの全体は，　(f＋g)(x)＝f(x)＋g(x)　(αf)(x)＝αf(x)なるベクトル演算と汎関数ノルム∥f∥によってバナッハ空間になる。…

【変分原理】より

…多くの場合，そのスカラー量はいくつかの物理量を含む時間･空間的な積分であり，それらの物理量が，時空変数の関数として変形を受けることに対し，積分値が最小値となるよううまくえらばれるという要請から，一定の方程式が導かれる。これらの物理量はこの変分原理の変分関数と呼ばれ，また変分関数を含む積分を汎関数という。場合によって変分関数は別の一定条件の制約下で変分されるよう要請されることがあり，これは束縛条件と呼ばれる。…

【変分法】より

…　問題を一般的に記述すると，ある条件(例えば上記の(2))を満たす関数の集合をΦとすれば，(1)はΦに属する関数y＝f(x)に対して一つの値Tを対応させる式であって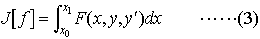，の形をしている。このような“関数の関数”を汎関数といい，与えられた関数の集合Φの中で，ある汎関数の値を最大または最小にする問題を変分法という。初めに述べたベルヌーイの問題が変分法の起りであるが，汎関数functionalという語はJ.アダマールの命名による。…

※「汎関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」