綴術算経 (てつじゅつさんけい)
建部賢弘が著した数学方法論の書。1722年(享保7)の序がある。内容は,探法則,探術理,探員数の3章に分け,各章を4条に分けて解説している。最後に〈自質の説〉と題して数学を勉強する心構えを述べ,中根元圭のくふうした問題,すなわち3辺が公差1の等差級数をなす整数値の三角形で,面積が有理数となる場合の解法を付録として終わっている。建部のいう綴術は帰納法のことで,帰納法こそ数学の問題を考える基本だとしている。本書は,(arcsin x)2のべき級数展開の方法が示されているので有名であるが,関孝和についての記述もあり,数学史上貴重な文献となっている。例えば,球の表面積を求めるのに,関は球を錐の集りとみて, として求め,建部はr+⊿rとrの二つの球を考えて,その体積の差を⊿rで割る。すなわち,
として求め,建部はr+⊿rとrの二つの球を考えて,その体積の差を⊿rで割る。すなわち,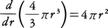 としたことなど興味深い記事が多い。
としたことなど興味深い記事が多い。
執筆者:下平 和夫
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
綴術算経
てつじゅつさんけい
建部賢弘(たけべかたひろ)の主著で、数学方法論について述べたもの。序文は1722年(享保7)、跋文(ばつぶん)は1725年。本書は、数学の問題を解くにあたっての心構えを説明している。彼の強調するところは帰納法である。法則、術理、員数を考えて、問題を解く方法をそれぞれ四問ずつに分けての説明がある。このなかに、円弧の長さの二乗を、直径と弓形の高さで表す無限級数が説明されているが、(sin-1x)2の世界で最初のマクローリン展開公式として有名である。また、本書には、建部の師である関孝和(たかかず)についても種々の記事があり、数学史上貴重な資料である。なお、本書の流布本は『不休綴術』といい、内容に少し違いがある。
[下平和夫]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
世界大百科事典(旧版)内の綴術算経の言及
【建部賢弘】より
…28年かかって1710年(宝永7)に《大成算経》(20巻)として完成した。賢弘の業績中特筆すべきは,22年(享保7)の序がある《綴術算経》である。この数学書は弟子に示した数学方法論で,帰納法がいかにたいせつであるかを論じている。…
※「綴術算経」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
 として求め,建部はr+⊿rとrの二つの球を考えて,その体積の差を⊿rで割る。すなわち,
として求め,建部はr+⊿rとrの二つの球を考えて,その体積の差を⊿rで割る。すなわち,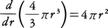 としたことなど興味深い記事が多い。
としたことなど興味深い記事が多い。
