非対称度（読み）ヒタイショウド（その他表記）measures of skewness

デジタル大辞泉

ひたいしょう‐ど【非対称度】

⇒歪わい度

出典　小学館

改訂新版　世界大百科事典

非対称度 (ひたいしょうど)
measures of skewness

歪（ひずみ）度ともいう。平均値を中心とする分布の非対称性の大きさと方向を示す量。数理統計学では分布の非対称度として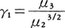，を用いることが多い。ここで，μ₂は平均mのまわりの二次モーメント（分散），μ₃は平均mのまわりの三次モーメントである。すなわち，今，問題とする分布に従う確率変数をXとすると，

　μ₂＝E［（X－m）²］

　μ₃＝E［（X－m）³］

である。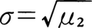とかく。分布がmに関して対称であればγ₁＝0となる。このγ₁は，分布が正規分布に近いとき，正規分布からのずれの大きさを与える尺度となっている。より詳しくいえば，確率変数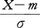の分布の特性関数と標準正規分布の特性関数の差は，｜γ₁｜が小さいほど小さくなる。

　K.ピアソンは，分布の非対称度を測る尺度として（m－モード）/σを提案した。このピアソンの尺度は，単峰分布に対して－\(\sqrt{3}\)以上，＋\(\sqrt{3}\)以下となることが知られている。ピアソンの尺度の与える非対称度の直観的イメージは明確であるが，一般に分布のモードを計算することはむずかしい場合が多い。

　そこで，ピアソンの尺度と上述のγ₁の関係を明らかにしなければならない。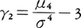

とおく。μ₄は平均mのまわりの四次モーメントである。ピアソン系の分布族に対しては，γ₁，γ₂が小さいとき近似的に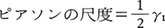，が成り立つことが知られている。
執筆者：清水 昭信

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

非対称度
ひたいしょうど
skewness

集団の構成を記述する統計的特性値の一つで，度数分布型の非対称の程度およびかたよりの方向を示すもの。度数分布が対称の場合，算術平均，中位数，並数 (最頻値) はすべて一致するが，非対称の場合，度数は並数の左右に均等に分布しない。並数が算術平均より小さい場合を非対称の方向が正であるといい，逆の場合を負であるという。通常非対称度 Sk は M を算術平均，Mo を並数，Me を中位数，σ を標準偏差とすると，Sk＝(M－Mo)/σ ，または，Sk＝3(M－Me)/σ で表わされる。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の非対称度の言及

【数理統計学】より

…p次モーメントμ_pは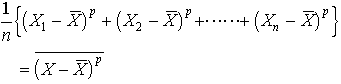と定義する。これらを用いて分布の非対称度(歪度)がμ₃²/μ₂³で，尖度がμ₄/μ₂²－3で定義され，いずれも分布の型をいうのに役だつ量である。
［関連度］
　各個体に2種類の標識があって，それらの値をX₁,X₂，……，X_n,Y₁,Y₂，……，Y_nとしよう。…

※「非対称度」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」