アイコナル（英語表記）eikonal

改訂新版　世界大百科事典

アイコナル
eikonal

幾何光学において，光学系を通って物空間から像空間への光線が通る道筋を与える関数。幾何光学の結像においては，物空間の1点P₀を通り屈折や反射を経て像空間の1点Pにいたる光線は，2点間の光学距離が最短になるような道筋を通る（フェルマーの原理）。これを数式で表すと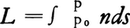，として，δL＝0となることを意味する（nは屈折率，sは光路の長さ）。この原理を偏微分方程式で表現すると｜grad V（P₀，P）｜²＝n²となり，nが与えられたときに光線が実際に通る道筋が得られる。この関数V（P₀，P）をアイコナルと呼ぶ。実質的にはW.ハミルトンが初めて導入したものであるが，その業績がうずもれてしまい，のちにH.ブルンスがそれとは独立に再発見した（1895）。アイコナルは解析的に幾何光学的結像を論ずるので便利であり，これを記述する独立変数としては，位置座標P₀（x₀，y₀，z₀），P（x，y，z）の組のほかに，光線の方向余弦にそれぞれの空間の屈折率をかけた光学的方向余弦（p₀，q₀，r₀）と（p，q，r）をとることもできる。前出のVは点アイコナルと呼ばれる（位置座標で表される）が，このほかに光学的方向余弦を用いる角アイコナルT（p₀，q₀；p，q），位置座標と光学的方向余弦の両者を用いる混合アイコナルW（p₀，q₀ ; x，y）およびW′（x₀，y₀ ; p，q）などがある。実際の光学系に対してアイコナルを厳密に求めることは難しいが，近似的にこれを求めて収差を解析的に論ずることができる。主光線のまわりに展開して2乗項までとると近軸光線束に関する結像公式が得られ，また4乗項までとるとザイデルのアイコナルが得られる。後者は共軸光学系の収差を分類して個々の性質を論ずるのに有効である。
執筆者：鶴田 匡夫

出典　株式会社平凡社「改訂新版　世界大百科事典」