グラスマン
ぐらすまん
Hermann Günther Grassmann
(1809―1877)
ドイツの数学者、言語学者。シュテッティン(現、ポーランドのシュチェチン)に生まれ、同地のギムナジウムの教師であった。もっとも著名な業績は大著『広延論』Ausdehnungslehreである。この書物は1844年に出版され、1862年にその改訂版が出たが、内容が当時の数学からあまりにもかけ離れ、記述も難解であったため、長い間無視されていた。グラスマンの業績が受け入れられるようになったのは、19世紀も終わりに近づいてからである。言語学では、インド・ヨーロッパ祖語の帯気音に関する「グラスマンの法則」を発見したほか、とくにインドの古典『リグ・ベーダ』Rigvedaに関するサンスクリット(梵語(ぼんご))の辞書は有名である。
[茂木 勇 2018年6月19日]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
グラスマン
Hermann Günther Grassmann
生没年:1809-77
ドイツの数学者,言語学者。オーデル河口近くの町シュテッティンで生まれ育った。父親が数学と物理を教えていたシュテッティンのギムナジウムで学び,その後ベルリンで神学を学んだ。1834年にベルリンの学校の数学の教師になり,36年にシュテッティンに帰り,ギムナジウムの数学,科学,宗教の教師になった。研究業績は数学,物理にわたり,数学についても代数,幾何,解析にわたる幅広いものであるが,もっとも重要なのは線形代数学の創設といえよう。線形代数学に関する著書《Die Ausdehnungslehre》は外積代数(グラスマン代数ともいう)も含んでいる。彼の構成が時代を超えてきわめて抽象的であったため,同時代の人々で彼の理論を理解できた人は少なかったという。53歳のとき数学をやめ,以後サンスクリットの研究にうちこみ,言語学上の業績を多くあげた。
執筆者:永田 雅宜
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
グラスマン
Grassmann, Hermann Günther
[生]1809.4.15. シュテッティン
[没]1877.9.26. シュテッティン
ドイツの数学者,言語学者。 1832年にシュテッティンのギムナジウムの教師となり,34年から 36年までベルリンの産業学校で教えたが,再びシュテッティンに帰り生涯同職にあった。数学者としては,現在グラスマン代数として知られているベクトル・テンソル計算の基礎を築いた業績で知られている。彼はこれを『広延論』 (1844) で展開したが,独特な記号や術語を用いて読みにくかったため当時は理解されなかった。言語学者としてはいわゆるグラスマンの法則を発見したことで知られている。ほかにサンスクリット語の研究がある。彼が編纂した『リグ・ベーダ』に関する辞書は現在でも広く使用されている。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内のグラスマンの言及
【幾何学】より
…同様に,空間の点は3個の実数の組で表され,座標が(x1,x2,x3),(y1,y2,y3)である2点間の距離は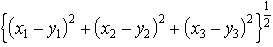 で与えられる。これを解析的に一般化しn個の実数の組(x1,x2,……,xn)を点として,2点(x1,x2,……,xn),(y1,y2,……,yn)の間の距離が
で与えられる。これを解析的に一般化しn個の実数の組(x1,x2,……,xn)を点として,2点(x1,x2,……,xn),(y1,y2,……,yn)の間の距離が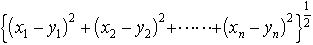 で与えられるn次元ユークリッド空間が,19世紀中期よりH.G.グラスマンらによって考えられるようになった。これにともなって,平面幾何学や立体幾何学がn次元ユークリッド幾何学に解析的に一般化され,また,射影幾何学や非ユークリッド幾何学もn次元の場合へ一般化された。…
で与えられるn次元ユークリッド空間が,19世紀中期よりH.G.グラスマンらによって考えられるようになった。これにともなって,平面幾何学や立体幾何学がn次元ユークリッド幾何学に解析的に一般化され,また,射影幾何学や非ユークリッド幾何学もn次元の場合へ一般化された。…
【線形代数学】より
…また,このころ,線形微分方程式の解の線形性が意識されるようになり,それに関連して一次独立という概念が意識された。このようないろいろな具体的対象から出発して,多くの人々,とくにA.ケーリーとH.G.グラスマンによって,高次元の場合を含めて明確化され,かつ抽象化された線形代数学が成長したのであり,これは19世紀中ごろのことである。ケーリーが座標に基礎を置いて扱ったのに対し,グラスマンは座標にこだわらずに理論構成をして,発展に大きく寄与した点に大きな特徴がある。…
※「グラスマン」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 


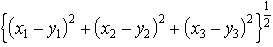 で与えられる。これを解析的に一般化しn個の実数の組(x1,x2,……,xn)を点として,2点(x1,x2,……,xn),(y1,y2,……,yn)の間の距離が
で与えられる。これを解析的に一般化しn個の実数の組(x1,x2,……,xn)を点として,2点(x1,x2,……,xn),(y1,y2,……,yn)の間の距離が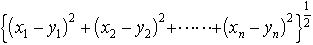 で与えられるn次元ユークリッド空間が,19世紀中期よりH.G.グラスマンらによって考えられるようになった。これにともなって,平面幾何学や立体幾何学がn次元ユークリッド幾何学に解析的に一般化され,また,射影幾何学や非ユークリッド幾何学もn次元の場合へ一般化された。…
で与えられるn次元ユークリッド空間が,19世紀中期よりH.G.グラスマンらによって考えられるようになった。これにともなって,平面幾何学や立体幾何学がn次元ユークリッド幾何学に解析的に一般化され,また,射影幾何学や非ユークリッド幾何学もn次元の場合へ一般化された。…