線形代数学（読み）センケイダイスウガク（その他表記）linear algebra

デジタル大辞泉

せんけい‐だいすうがく【線形代数学】

ベクトル空間およびその一次変換に関する理論を扱う代数学の一部門。

出典　小学館

精選版 日本国語大辞典

せんけいだいすう‐がく【線形代数学】

1. 〘 名詞 〙 線形空間および線形写像に関する代数的理論。行列や行列式が重要な役割を演ずる。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

線形代数学 (せんけいだいすうがく)
linear algebra

線形はlinearの訳語で線型とも書く。直線の方程式が一次式であることから，一次式に関連するものにlinearという語を用いることが多い。したがってlinearの訳語として一次が使われることも多い。一次独立と線形独立，一次写像と線形写像がそれぞれ同義であるのはその例である。線形代数学で扱う主対象は線形空間（ベクトル空間），ベクトル，線形写像，アフィン空間，線形変換，行列，行列式，連立一次方程式などである。これらが主対象である理由は，これらの発生，発展が一次式に関連してなされてきたことにあるといえるが，その点をもう少し詳しく述べよう。実用計算において一次式を利用することは多い。そのため一次方程式，連立一次方程式は古代から実用計算において重要であった。他方，数学的問題を考える際に，その問題に適した座標変換，あるいは変数変換などを利用することが古来試みられてきた。解析幾何の問題で，与えられた座標のままでは計算が複雑であるが，適当な座標変換をすれば計算がやさしくなることがあるのは，しばしば経験するところであろう。積分の計算における置換積分は一種の変数変換である。このような変換のうち，いちばん基礎的であるのが，一次変換であるといえよう。また，近似という面から考えても，重要な第一次近似が一次式で得られるのがふつうである。このような理由で，一次式，一次変換は古来重要な役割を果たしてきたのであり，数学の発展とともに，これらに関連する諸概念が明確化され，抽象化されて線形代数の対象になったのである。ベクトル空間は，その構成要素であるベクトルの間の関係式として，一次式で与えられるものを考えることによって得られたものであり，アフィン空間，線形変換などはベクトル空間と密接な関連をもつのである。行列は線形変換と本質的には同じである。行列式は，連立一次方程式に関連して発生したものであるが，それ以外に，行列の理論に重要な位置を占めるのである。なお，線形代数で扱う線形空間は有限次元であるとは限らないが，有限次元の場合が基本的である。また，例えば，2x₁y₁＋3x₂y₁＋4x₁y₂＋x₂y₂は，x₁，x₂についても，y₁，y₂についても一次斉次式である。このように2組のもの，例えば2組の変数（x₁，x₂，……，x_n）と（y₁，y₂，……，y_n）のいずれについても一次斉次式であるとき，これら2組のものについて双一次であるという。双一次であるものの典型的な例には後述のテンソル積がある。双一次のものも線形代数の対象に含めるのがふつうである。

歴史

バビロニア，中国のいずれの文明においても古代から連立一次方程式の解法が知られていたが，17世紀になって，ようやく連立一次方程式の解法に関連して行列式が生まれた。和算では，関孝和が3次（3行3列）までの行列式は正しく扱ったが，4次以上は誤っていた。それに対し，井関知辰は1690年発行の《算法発揮》で正しく扱った。これが行列式を正しく扱った世界最古の文献であると考えられている。西洋ではG.W.F.ライプニッツが93年に書いた手紙の中に，行列式を考えたことを示す記述があるのが最古のように思われるが，そこには詳しい説明もないので，正しいものを考えたかどうかはわからない。そこで1750年に明確に述べたクラメールが行列式の創始者とみなされているが，井関知辰におくれること60年といえる。

　他方，P.deフェルマーはR.デカルトよりも先に，曲線を方程式で分類することを考え，曲線とその次数との関係を調べた。そのような考えに基盤を置いて18世紀における解析幾何の開花が得られたといえようが，解析幾何には線形性がいろいろな形でかかわっているため，線形変換に関連して行列式が明確化された。また，このころ，線形微分方程式の解の線形性が意識されるようになり，それに関連して一次独立という概念が意識された。このようないろいろな具体的対象から出発して，多くの人々，とくにA.ケーリーとH.G.グラスマンによって，高次元の場合を含めて明確化され，かつ抽象化された線形代数学が成長したのであり，これは19世紀中ごろのことである。ケーリーが座標に基礎を置いて扱ったのに対し，グラスマンは座標にこだわらずに理論構成をして，発展に大きく寄与した点に大きな特徴がある。例えばベクトルの一次独立性を明確に定義し，ベクトル空間の次元についての等式dim （U＋V）＋dim（U∩V）＝dim U＋dim Vを導いたのはグラスマンである。またグラスマンは実数体上のベクトル空間の外積代数を定義した。したがって外積代数はグラスマン代数とも呼ばれるのであるが，これは行列式の扱いにも有用である。いわゆる行列式の公理的定義（n次正方行列Aに対し行列式の値を対応させる関数と考えて，（1）Aが単位行列なら値は1，（2）二つの行を入れかえれば値は－1倍になるなどの性質で定義する方法）は外積代数の構成に含まれているともいえる。その後も，多くの数学者により，種々の線形性をもった具体的な対象がとり上げられ，それらが抽象化されて線形代数学の中にとり入れられて発展してきた。一方，古くは，線形代数学で扱う対象は，実数体というような特定の体の上での考察であったが，それらを一般の体の上の考察に一般化しても，ほとんどの場合，同じ議論で一般化される。近年はもっと一般に，環の上での考察にまで一般化して考察することも多い。その意味で，線形代数学と加群の理論との境界は定められない。

双線形写像

以下では，可換環Aの上の加群の場合について述べるが，例えば，ベクトル空間の場合ならば，Aが基礎の体で，加群といっているのがベクトル空間と思えば同様である。非可換環の上の加群の場合には，右加群，左加群の区別が必要なのでもう少し複雑になるので割愛する。

　Aが可換環で，M，N，LはA加群であるものとする。MとNとの直積M×NからLへの写像fが双線形（双一次）写像であるとは，任意のx，x′∈M，y，y′∈N，a∈Aに対して，次の3等式が成り立つときにいう。

　f（x＋x′，y）＝f（x，y）＋f（x′，y）

　f（x，y＋y′）＝f（x，y）＋f（x，y′）

　f（ax，y）＝f（x，ay）＝af（x，y）

　任意のx，yについて，f（x，y）＝0であれば双線形であるが，これはつまらない双線形写像である。像が0になるようなx，yの組がいちばん少ないような双線形写像があり，それを具体的に構成しうるのが，次に述べるテンソル積tensor productである。テンソル積の一つの構成法は各x∈Mおよびy∈Nに対して，f（x，y）＝x⊗yが双線形写像であるような，必要最小限の関係を導入するのであるといいうる。ていねいに述べれば，直積集合M×N＝｛（x，y）｜x∈M，y∈N｝を使って，A係数の有限和の形の元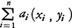，を形式的に考え，これらの作る加群Fにおいて，（x＋x′，y）－（x，y）－（x′，y），（x，y＋y′）－（x，y）－（x，y′），（ax，y）－a（x，y），（x，ay）－a（x，y）の形の元全体で生成された部分加群Iをとり，F/IをMとNとのテンソル積M⊗_aNと定めるのがある。（x，y）の属する剰余類をx⊗yで表すのである。M⊗_aNはこのようなx⊗yで生成されたA加群になる。M′，N′がA加群で，φ：M→M′，ψ：N→N′が準同型であれば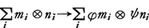，はM⊗_aNからM′⊗_aN′の中への準同型になる。これをφ，ψのテンソル積といい，φ⊗ψで表す。行列のクロネッカー積と呼ばれるものがあるが，これは，二つの行列A，Bが与える線形写像f_a，f_bのテンソル積f_a⊗f_bに対応する行列である。テンソル積に関しては，次の定理がもっとも基本的である。

定理

A加群M，Nの直積M×NからA加群Lの中への双線形写像fがあれば，M⊗_aNからLの中への準同型φであって，f（m，n）＝φ（m⊗n）がすべての（m，n）∈M×Nについて成り立つものが，ただ一つ存在する。

　テンソル積の例についてつけ加えよう。

　例1　M⊗_aAはMと同一視できる。

　例2　p，qが互いに素な整数であるとき，（Z/_pZ）⊗_z（Z/_qZ）＝｛0（＝0⊗0）｝。ただし，Zは有理整数環である（理由：1＝pa＋qbとなる整数a，bがあるから，m⊗n＝（pa＋qb）m⊗n＝pam⊗n＋qbm⊗n＝0＋bm⊗qn＝0）。

　例3　Mがa₁，a₂，……，a_mを一次独立基にもつ自由加群で，Nがb₁，b₂，……，b_nを一次独立基にもつ自由加群であれば，M⊗_aNは｛a_i⊗b_j｜i＝1，2，……，m;j＝1，2，……，n｝を一次独立基にもつ自由加群である。無限個の元からなる一次独立基をもつ場合も同様である。この結果はAが体である場合によく利用される。
執筆者：永田 雅宜

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

線形代数学
せんけいだいすうがく
linear algebra

線型代数。代数学の一部門で，ベクトル空間とその線形写像を中心とする理論を研究する。いわば1次式の理論と応用である。線形代数には，行列や行列式の理論も含まれるが，それは，有限次元ベクトル空間に基底を定めれば，線形写像がすべて行列で表わされるからである。ベクトルや行列の理論は，数学のあらゆる分野において基礎的な役割をもつばかりでなく，また応用上でも，物理学，工学，統計学，経済学，数理計画法など広い分野に利用されている。それは比例関係にある (あるいはそうみなしてよい) 現象が多いことと，理論が簡単なため，さらに複雑な現象の研究のための出発点とされるからである。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の線形代数学の言及

【数値解析】より

…数値計算法とか実用解析などの名まえでも呼ばれており，行列の計算や微分方程式の解法など広く科学の諸分野に現れる問題を数値的に取り扱うことを目標とする。そこでは数学における古典解析学が主要な手段を提供しているが，最近は各種の計算機を用いた機械計算の飛躍的発展に伴い，それに応じた種々の技法が開発されている。数値解析の具体的な課題としては，問題の近似解を数値的に求めること，その近似解の性質，有効な数値計算の手順，真の値と近似解との理論的な差，丸めの誤差などの評価などである。…

※「線形代数学」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」