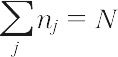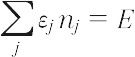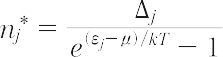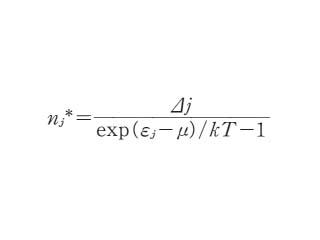ボース=アインシュタイン分布 (ボースアインシュタインぶんぷ)
Bose-Einstein distribution
有限の空間の中に閉じ込められたボース粒子の集団を考える。相互作用は無視できるとしよう。定常状態では,各粒子は量子状態0,1,2,……のいずれかをとる。これらの量子状態はエネルギー固有状態である。量子状態j(j=0,1,2,……)のエネルギーをεjと書くことにする。ε0は基底状態のエネルギーを表すとする。状態jを占めている粒子の数njを観測すれば,1回の観測では,0を含む正の整数のいずれかの値になるが,粒子集団が絶対温度Tの熱平衡状態にある場合,njの平均値〈nj〉は,
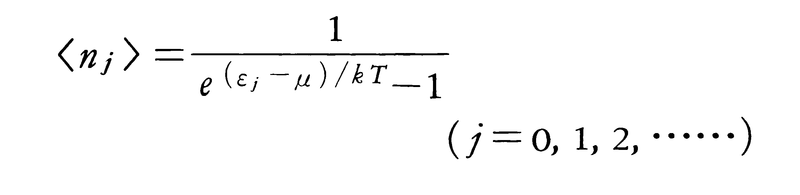
で与えられる。これをボース=アインシュタイン分布という。ここにkはボルツマン定数で,μは化学ポテンシャルと呼ばれるもので,〈n0〉+〈n1〉+〈n2〉+……が与えられたボース粒子の総数Nに等しくなるという条件で決まる。したがってμはTの関数となる。
相互作用のないボース粒子N個が体積Vの箱の中に閉じ込められている場合,Tが,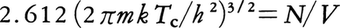 で与えられる温度Tcより高ければ,μ<ε0≅0であって,上記のボース=アインシュタイン分布の公式はすべての量子状態に対して成立する。Tc以下の温度では,最低エネルギーε0の状態を占める粒子数n0だけは,上の公式では与えられず,特別扱いしなければならぬ。このときn0だけはずぬけて大きく,ボース=アインシュタイン凝縮が発生する。
で与えられる温度Tcより高ければ,μ<ε0≅0であって,上記のボース=アインシュタイン分布の公式はすべての量子状態に対して成立する。Tc以下の温度では,最低エネルギーε0の状態を占める粒子数n0だけは,上の公式では与えられず,特別扱いしなければならぬ。このときn0だけはずぬけて大きく,ボース=アインシュタイン凝縮が発生する。
空洞中の光子(フォトン)や固体中の音量子(フォノン)のように粒子数が一定でないボース粒子の熱平衡分布は,上のボース=アインシュタイン分布式の中でμ=0とおいた公式で記述される。これはプランクの分布式と呼ばれている。
ボース=アインシュタイン分布の概念が役だつ具体的な例としては,2K前後ないしそれより低温領域での4Heの液体をあげることができる。4He原子相互間に強い斥力があるので,ボース=アインシュタイン分布式は近似式でしかないが,これによって量子液体4Heの一つの重要な側面がとらえられている。
ボース粒子のボース=アインシュタイン分布は,フェルミ粒子のフェルミ=ディラック分布に対応するもので,ともに量子性に由来する。高温,低密度では量子性が薄れ,いずれの分布もマクスウェル=ボルツマン分布に帰着する。
執筆者:伊豆山 健夫
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
ボース-アインシュタイン分布
ボースアインシュタインブンプ
Bose-Einstein distribution
ボース統計にもとづく状態の数W{nj}から,系の全粒子数一定,
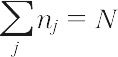
全エネルギー一定,
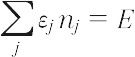
の条件のもとに,平均粒子数{nj*}が次のように求められる.
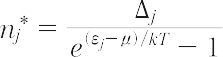
ただし,kはボルツマン定数,Tは絶対温度,Δj はエネルギー準位 εj にある状態の数,μは粒子数Nが一定という条件から決まるパラメーターで,化学ポテンシャルに等しい.この分布をボース-アインシュタイン分布またはボース分布という.上式からわかるように,μ = 0のときには εj が0に等しい状態に対して,nj* は無限に大きくなる.これは理想ボース気体では運動エネルギーが0である最低の量子状態にNと同じ程度の数の粒子が入ってしまうことに対応しており,一種の凝縮現象と考えられる(ボース-アインシュタイン凝縮).ここでいう凝縮は,単に量子状態での粒子分布について起こる現象で,気相から液相への分離のように空間的に相が変わるものではない.[別用語参照]量子統計力学
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
Sponserd by 
ボース‐アインシュタイン分布【Bose-Einstein distribution】
ボース‐アインシュタイン統計*に基づく状態の数は W(nj)となるが,系の全粒子数 ∑nj=N,全エネルギー一定条件(∑njεj=E)という条件から,平衡分布は下のようになる.
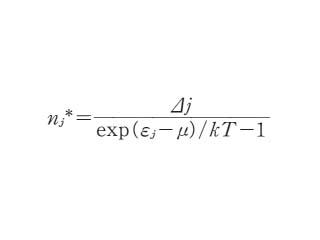
ここで ⊿j はエネルギー準位 εj にある状態の数,μ は化学ポテンシャルに相当する.
ある温度以下で μ がゼロとなると,εj が0に等しい状態に対して nj* が無限に大きくなることになる.つまり最低のエネルギー準位に N と同程度の粒子が収容される.これは,ボース‐アインシュタイン凝縮*と呼ばれる状態である.
出典 朝倉書店法則の辞典について 情報
Sponserd by 
ボース=アインシュタイン分布
ボース=アインシュタインぶんぷ
Bose-Einstein distribution
温度 T で熱平衡状態にあるボソンの系において粒子間の相互作用が無視できるときに,粒子がエネルギー ε の状態にある確率,またはこの状態にある粒子の平均数は次式で与えられる。
f(ε)=1/{ exp [(ε-μ)/kT]-1}
この分布をボース=アインシュタイン分布またはボース分布という。 k はボルツマン定数,μ は化学ポテンシャルである。光子やフォノンは粒子が生成,消滅して全粒子数が一定でないので μ=0 になる。プランクの放射式はこの分布を光子に適用して得られる。また粒子密度が小さく,温度が高い場合にこの分布はマクスウェル=ボルツマン分布に近づき,その逆の場合はボース=アインシュタイン凝縮を示す。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
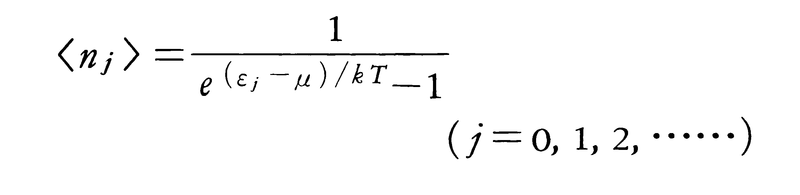
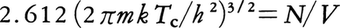 で与えられる温度Tcより高ければ,μ<ε0≅0であって,上記のボース=アインシュタイン分布の公式はすべての量子状態に対して成立する。Tc以下の温度では,最低エネルギーε0の状態を占める粒子数n0だけは,上の公式では与えられず,特別扱いしなければならぬ。このときn0だけはずぬけて大きく,ボース=アインシュタイン凝縮が発生する。
で与えられる温度Tcより高ければ,μ<ε0≅0であって,上記のボース=アインシュタイン分布の公式はすべての量子状態に対して成立する。Tc以下の温度では,最低エネルギーε0の状態を占める粒子数n0だけは,上の公式では与えられず,特別扱いしなければならぬ。このときn0だけはずぬけて大きく,ボース=アインシュタイン凝縮が発生する。