量子統計（読み）りょうしとうけい

改訂新版　世界大百科事典

量子統計 (りょうしとうけい)

統計力学とは，熱力学的対象の力学構造を知ることにより，その熱力学を決めていく学問であるが，対象となる系の力学構造が本質的に量子力学である場合の統計力学を量子統計力学quantum statical mechanicsといい，量子統計力学で用いられる統計的手法を量子統計と呼ぶ。

　物理量fの熱力学的観測値f-は，古典統計力学では，対象となる系の力学状態を表す位相空間内でのfの平均値にすり代えられる。これがエルゴード定理である（エルゴード理論）。対象が孤立系（外界との間にエネルギーのやりとりも粒子のやりとりもない系）なら，位相空間内の等エネルギー面上でのfの平均値である。量子力学では，古典力学の位相空間という概念は役だたず，かわりにヒルベルト空間が登場し，系の量子状態はヒルベルト空間内の単位ベクトルで表される。一つの熱平衡に対応する量子状態は多数あるが，一つの熱平衡状態における熱力学的観測値はユニークに決まる。こうした諸事実からの論理的帰結は次のようになる。すなわち量子統計ではfの熱力学的観測値は，

　f-＝Tr｛fρ｝

で与えられる。ここにTrはヒルベルト空間内での対角和を意味する。物理量fはヒルベルト空間内での演算子あるいは行列といってもよい。ρも演算子あるいは行列で密度行列といい，一つの熱平衡状態に一つのρが対応すると考え，Trρ＝1となるように選ばれる。系のハミルトニアン（エネルギー演算子）の固有値をE_n，これに対応する固有ベクトルをΨ_nとする（n＝0，1，2，……）。これによってρをマトリックス表示すると，熱平衡状態ではρは対角形で，対角成分ρ_nnはE_nにしかよらない。fも｛Ψ_n｝によってマトリックス表示すると，となる。f_nnは対角成分である。内部エネルギーの値がUとU＋⊿Uの間にある孤立系では，U≦E_n≦U＋⊿Uのときρ_nnは正の定数で，そうでないとき（E_n＜UやE_n＞U＋⊿Uのとき）は ρ_nn＝0ということになる。温度Tの熱浴と接している系（等温系）では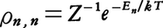，すなわち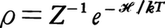，である。ここで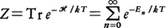，で，kはボルツマン定数である。以上が量子統計の第一歩である。

　エントロピーSは，孤立系ではボルツマンの原理，一般にS＝－kTr｛ρlnρ｝で与えられる。量子統計の特徴の一つは，T→0のときにS→0が期待されることである。これは熱力学の第3法則と呼ばれ，量子力学以前にネルンストによって見いだされている。それは一般に量子系の基底状態の縮重度が，たかだか粒子数Nのオーダーで，2ⁿのような巨大な縮重はありえないことに起因する（ランダム系のように準安定でしかない状態を扱う場合には，第3法則が破れる可能性もある）。古典論で成り立つマクスウェル=ボルツマンの速度分布則（マクスウェル=ボルツマン分布）は量子統計では破れる。より大きな特徴として，古典論では運動エネルギー部分の統計熱力学が粒子間相互作用部分のそれと完全に独立であって，前者はきわめて簡単であったのに反し，量子統計では両者は分離できないということがある。これは量子力学では，運動エネルギーと位置エネルギーとが，代数的な意味で〈交換〉しないことに由来する。さらに，相互作用がない多粒子系でも，量子系ではマクスウェル=ボルツマンの速度分布が破れるのである。

　量子論に登場する粒子は，フェルミ粒子（フェルミオンfermion）かボース粒子（ボソンboson）かに大別される。いずれの場合も同種の粒子はまったく識別不可能で，2個の同種粒子を入れ替えても量子状態は不変だと考える。しかし元来，波動関数には位相因子の不定性があり，2粒子交換により波動関数は±1の位相因子だけ変わってよいことになる。フェルミ粒子とは，2粒子交換の際に多粒子系の波動関数の符号だけが変わるような粒子のことで，スピンが半奇数の粒子や複合粒子，たとえば電子や陽子，中性子，質量数が奇数の原子核などがこれに属する。ボース粒子は，2粒子交換で波動関数が（符号を含め）まったく不変であるような粒子のことであり，これにはスピンが整数の素粒子や複合粒子，すなわちπ中間子，フォトン，質量数が偶数の原子核などが属する。このことから，フェルミ粒子の場合は一つの粒子状態を占める粒子数は0または1に限られる（フェルミ=ディラック統計，またはフェルミ統計という）。一方，ボース粒子の場合は一つの粒子状態が収容できる粒子数は0，1，2，3，……と限りがない（ボース=アインシュタイン統計，またはボース統計という）。

　相互作用のない多粒子系が温度Tの熱平衡状態にある場合，エネルギーεの1粒子状態jにいるフェルミ粒子の数n_jは平均して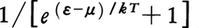，であり，ボース粒子なら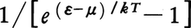，である（μは化学ポテンシャル）。前者はフェルミ=ディラック分布，後者はボース=アインシュタイン分布と呼ばれ，いずれも，

　〈n_j〉＝Tr｛ρn_j｝

によって求められる（〈　〉は平均の意味）。

　低温ないし高密度，すなわち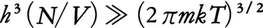，のとき（hはプランク定数，Nは粒子数，Vは粒子の動き回れる体積），フェルミ粒子はほとんどフェルミ縮退しており，ボース粒子は最低準位j＝0に凝縮（ボース=アインシュタイン凝縮）がみられる。金属中の伝導電子は常温ではフェルミ縮退しており，金属が融ける温度よりずっと高温にならないとボルツマン統計は使えない（水銀のように融点の低いものもあるが，常温でフェルミ縮退しているのはまちがいない）。こうした縮退ないし凝縮ゆえにフェルミ粒子集団もボース粒子集団も，低温での比熱がT→0とともに0となり，熱力学の第3法則は保証されている。

　粒子間に相互作用があると，フェルミ=ディラック分布やボース=アインシュタイン分布はそのままの形で成立するはずはないが，相互作用が斥力なら，フェルミ縮退ないしボース=アインシュタイン凝縮の特徴は保持されている。この縮退あるいは凝縮の概念が量子統計の最大の特色と成果といえる。
→統計力学
執筆者：伊豆山 健夫

出典　株式会社平凡社「改訂新版　世界大百科事典」