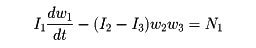オイラーの運動方程式
オイラーのうんどうほうていしき
Euler's equation of motion
(1) 完全流体に対する運動方程式。流体の速度ベクトルを u ,圧力を p ,密度を ρ ,流体の単位質量あたりに働く外力ベクトルを K とすれば,完全流体に対して次の運動方程式が成り立つ。
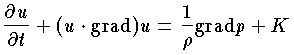 これをオイラーの運動方程式という。完全流体においては,この方程式と,連続の方程式および流体の状態方程式 ρ=f(p) とを連立させて,与えられた初期条件および境界条件のもとで解けば,未知関数 u ,p ,ρ が求められ,それにより流体の運動が決定される。
これをオイラーの運動方程式という。完全流体においては,この方程式と,連続の方程式および流体の状態方程式 ρ=f(p) とを連立させて,与えられた初期条件および境界条件のもとで解けば,未知関数 u ,p ,ρ が求められ,それにより流体の運動が決定される。
(2) 固定点または重心のまわりの,剛体の回転運動を決める運動方程式。剛体の回転運動の方程式は非常に複雑であるが,剛体に固定されて剛体とともに回転する座標系で表わすと比較的簡単になる。特に回転の中心に関する3つの慣性主軸を座標軸とする回転座標系で表わした最も単純な方程式がオイラーの運動方程式である。主慣性モーメントを I1 ,I2 ,I3 ,回転角速度の成分を ω1 ,ω2 ,ω3 ,外力のモーメントの成分を N1 ,N2 ,N3 とすれば,オイラーの運動方程式は対称的な次の3式で与えられる。
I1(dω1/dt)-(I2-I3)ω2ω3=N1
I2(dω2/dt)-(I3-I1)ω3ω1=N2
I3(dω3/dt)-(I1-I2)ω1ω2=N3
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
オイラーの運動方程式
おいらーのうんどうほうていしき
ニュートンの運動法則を用いて導いた剛体の回転運動に関する方程式をいう。このほか、粘性のない完全流体に関する運動方程式もオイラーの運動方程式という。いずれも、スイス生まれの数学者・物理学者であるオイラーが導出したものである。ここでは剛体に関する運動方程式について述べる。
剛体を無限個の質点の集まりとみることにすれば、ニュートンの運動の法則から、剛体の回転運動の運動方程式を導くことができる。剛体は他から作用を受けても内部状態の変化しない理想的な物体であって、その回転運動の運動方程式を求めるのに、この特徴に注目して、剛体に固定した座標系を用いる。このとき、運動方程式にはコリオリの力が現れる。また、質点の質量のかわりに、剛体の質量分布と座標軸で決まる慣性モーメントIを、また、質点に働く力のかわりに力のモーメントNを用いることになる。次式は、x軸の周りの角速度ωの時間変化を与えるオイラーの運動方程式である。
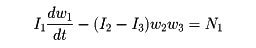
ここで1、2、3の添え字は、それぞれx、y、z軸に関する量であることを示す。
[田中 一]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
法則の辞典
「オイラーの運動方程式」の解説
オイラーの運動方程式【Euler's equation of motion】
一点で固定された剛体について,その主軸に固定した座標系における運動方程式.次のような三つの方程式である.
Ixxωx+(Izz-Iyy)ωyωz=Lx
Iyyωy+(Ixx-Izz)ωxωz=Ly
Izzωz+(Iyy-Ixx)ωyωx=Lz
ここで Iii は慣性モーメント,Lj は主軸まわりの力のモーメント,ωk は固定座標軸に対する回転角度の各成分を表している.
出典 朝倉書店法則の辞典について 情報
Sponserd by 
世界大百科事典(旧版)内のオイラーの運動方程式の言及
【運動】より
…この方程式は剛体を微小部分(または質点)に分け,そのおのおのについてたてた(1)および(2)式の形の運動方程式から導くことができる。固定点のあるときの剛体の運動は,剛体の位置を指定するのに三つの角度(例えばオイラー角)が必要なため,その変化を与える(4)式の形の三つの連立方程式(角運動量ベクトルLの変化を与えるオイラーの運動方程式。ここではLやNはベクトルに変わる)を解いて定めねばならない。…
【運動方程式】より
…回転運動を剛体に固定した座標系,とくに慣性の主軸に選んでやれば,(2)″はオイラーの方程式と呼ばれるものになる。[回転運動](c)流体の運動方程式 流体の場合も,その微小部分に着目することによって,(1)の運動方程式から流体に対するラグランジュの運動方程式またはオイラーの運動方程式を導くことができる。両者の差異は流体の運動の記述のしかたの違いにより,前者では流体の微小部分の運動を追究し,また後者では各瞬間における流体各点での速度,圧力,密度の値,すなわちこれらの量の場を求める。…
※「オイラーの運動方程式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
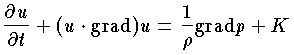 これをオイラーの運動方程式という。完全流体においては,この方程式と,連続の方程式および流体の状態方程式 ρ=f(p) とを連立させて,与えられた初期条件および境界条件のもとで解けば,未知関数 u ,p ,ρ が求められ,それにより流体の運動が決定される。
これをオイラーの運動方程式という。完全流体においては,この方程式と,連続の方程式および流体の状態方程式 ρ=f(p) とを連立させて,与えられた初期条件および境界条件のもとで解けば,未知関数 u ,p ,ρ が求められ,それにより流体の運動が決定される。