回転運動（読み）カイテンウンドウ（英語表記）rotation

デジタル大辞泉

かいてん‐うんどう〔クワイテン‐〕【回転運動】

物体あるいは質点系が、相互の相対的位置を変えずに、一定の軸のまわりを回る運動。

出典　小学館

精選版 日本国語大辞典

かいてん‐うんどうクヮイテン‥【回転運動】

1. 〘 名詞 〙 物体または質点が、ある一定の点や直線のまわりを一定角だけまわること。あるいはまわりつづけること。または、まわす操作。回転。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

回転運動 (かいてんうんどう)
rotation

太陽の周りの惑星の運動のように，大きさを考えず1点で表した物体（質点という）が他の1定点の周りで行う円運動や楕円運動をいうこともあるが，大きさのある物体の（変形を別途に考えることにして）運動を，並進運動と回転の合成として取り扱う場合の後者を指すのがふつうである。例えば，机の上を転がる円筒を考えると，その運動は軸の平行移動とその周りの回転とを合わせたものとみなすことができる。この場合，各瞬間の運動を，円筒と机の接触線を軸とした回転と考えることも可能である。そうすると回転軸は次々と移り変わることになる。回転を考えるときには物体の変形を無視しているから，物体に固定した座標軸O′-ξηζをとり，その原点O′が空間に対してどう運動するかで並進運動を表し，空間に固定したx，y，z軸の方向とξ，η，ζ軸の方向との角の関係によって回転を表すと便利である。物体の1点が固定されているときにはその点をO′にとるとつごうがよいが，固定点がないときには重心（質量中心）をO′にとると便利なことが多い。方位を表すのによく用いられるのは，図に示す三つの角θ，φ，ψで，これをオイラー角という。x′，y′，z′軸は，O′を通って空間に固定されたx，y，z軸に平行に引いた直線である。こまの運動などはこれを使って論ぜられるが相当に複雑である。

　以下，単純な固定軸の周りの回転について考えると各瞬間の運動は角速度ωで決まる。物体を細分したと考えてその一片の質量をm_i，回転軸からの距離をr_iとすると，その速さはr_iω，運動量はm_ir_iω，軸の周りの角運動量はm_ir_i²ωとなるので，物体のもつ全角運動量はL＝Iωと表すことができる。ただし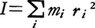，は軸の周りの慣性モーメントである。Lを変化させるのは外力のモーメント（の和）Nであり，dL/dt＝Nの関係が成り立つ（tは時間）。外力がないか，あっても作用線が回転軸を通る場合には，Lは一定に保たれる。これらの関係は，並進運動の運動法則における質量，速度，運動量，力をそれぞれ慣性モーメント，角速度，角運動量，力のモーメントに置き換えたものに対応しており，運動エネルギーも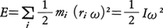で与えられる。並進運動の慣性に対応するのは，全角運動量Lあるいは角速度ωを一定に保とうとする性質であり，これを利用すると慣性モーメントの大きいはずみ車を用いてエネルギーを蓄えることが可能である。
執筆者：小出 昭一郎

図－回転運動を表すオイラー角

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

回転運動
かいてんうんどう

質点または質点の集まり、もしくはその特別なものとしての剛体が、固定点ないしは回転軸から距離および相互の位置を変えずに行う運動のこと。回転運動を考えるとき、慣性系に対して回転する座標系を考えると便利な場合がある。このような座標系を回転座標系という。静止という概念は絶対的なものではない。たとえば回転しているメリーゴーラウンドに乗っている人にとっては周囲の風景のほうが回転しているように見える。運動のありさまを記述するということだけ考えるならば、大地とメリーゴーラウンドのどちらが静止しているかを決める決め手はない。いいかえれば、どのような座標系も運動学的には平等である。回転運動には、たとえば太陽の周りの惑星の運動や地球の自転、またこまの運動のように、それ自身の心棒の周りに自転しているほかに、その心棒が鉛直線の周りに回転する歳差運動、さらに心棒の傾きの変化を伴う章動とよばれる複雑な回転運動もある。

　回転系においては、慣性系において与えられた力のほかに次の3種類の見かけの力（慣性力）が現れる。(1)mr×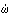　角速度ベクトルωが時間とともに変化する場合にのみ現れる力で、特別に名前はついていない。(2)2m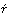×ω　コリオリの力。質点の回転系における速度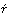と角速度ベクトルの両方に垂直な力である。(3)mω×(r×ω)　遠心力。大きさはmρω²で方向は回転半径ベクトルρの向きに一致している。mは質点の質量、rは質点の位置ベクトル、その上の点は時間の第一微係数（すなわち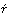=dr／dt）、×はベクトル積を表す。回転が一様ならば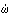=0なので(2)および(3)の力だけとなる。質点が回転系に対して静止すれば(2)の力は消えて遠心力のみとなる。

［村岡光男］

[参照項目] | 遠心力 | コリオリの力

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

回転運動
かいてんうんどう
rotational motion

物体のすべての点が1つの固定点 (固定軸) を中心 (中心軸) とする同心球 (同軸円柱) 面上を同じ角速度で動く運動を，その固定点のまわりの回転運動という。軌道は完全に閉じなくても，また周期が徐々に変化してもよい。

出典　ブリタニカ国際大百科事典 小項目事典