ビオ‐サバールの法則
びおさばーるのほうそく
Biot-Savart's law
磁界(磁場)、とくに静磁界の基本法則。1820年にフランスのビオとF・サバールによって発見された。磁界には磁石から発生するものと電流から発生するものとがあるが、両者の間には区別がなく、今日の理論体系では、磁石といえどもそれと等価な電流を基本とする考え方が主流になっている。ビオ‐サバールの法則は、与えられた電流回路から発生する磁界を求める基本関係を示すものである。この法則は、電気の基本法則であるクーロンの法則と同じく遠隔作用的な表現になっており、場としての表現を使うと、(1)磁束はかならず閉じた形になっており、また、(2)アンペールの法則に書き直せる。しかし、ビオ‐サバールの法則はコイルがつくる磁界などを計算するときに依然として重要な公式である。電流が流れるような電流回路はかならず閉じた回路をつくっており、その全体から発生した磁界しか観測することができない。図の回路上の小部分ABを含む平面上のP点に垂直に右ねじを立て、それをABからAPの向きに回したときに右ねじが進む方向が磁界の向きとなる。正しい磁界の大きさΔHは
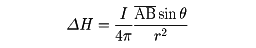
によって与えられる。回路全体から発生する磁界は、ビオ‐サバールの法則で与えられる磁界をベクトル的に積算することによって求められる。
[山口重雄]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
改訂新版 世界大百科事典
「ビオ‐サバールの法則」の意味・わかりやすい解説
ビオ=サバールの法則 (ビオサバールのほうそく)
Biot-Savart's law
導体を流れる電流の微小部分が周囲につくる磁場を与える法則。電流I(A)の流れている導線を長さの方向に細分し,その微小な長さds(m)の部分の電流素片Idsが,素片のある場所Oからr(m)の距離にあるP点につくる磁場の強さdH(A/m)は,dH=Isinθds/4πr2で表されるというもの(図参照)。ここにθは,OPとO点における電流Iとのつくる角である。1820年にフランスのJ.B.ビオとF.サバールによって与えられた。実際には電流は連続したものであるから,P点における磁場の強さは,電流素片によって生ずる磁場dHを電流の道筋に沿って素片の位置について積分して与えられる。この法則で簡単に計算できる例としては,半径r(m)の円電流I(A)が中心につくる磁場がある。すなわち,θ=π/2でsinθ=1,またrはすべて半径rに等しいので,H=I×2πr/4πr2=I/2r(A/m)となる。
執筆者:近角 聡信
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
ビオ=サバールの法則
ビオ=サバールのほうそく
Biot-Savart's law
定常電流がつくる磁場についての法則。 1820年フランスの J. B.ビオと F.サバールが定量的な実験をもとにして,見出した。導線を流れる電流 I が点Pにつくる磁場 H の大きさは,電流の微小部分 Ids からの寄与 dH の総和で与えられ,次のように表わされる。
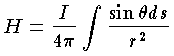 r は回路の微小要素 ds からPまでの距離で,θ は ds と r とのなす角。磁場の向きは電流の進む向きに右ねじを回すときのねじの回転方向になる。電流がつくる磁場については,ビオ=サバールの法則のほかにアンペールの法則もあるが,いずれか一方より他方が導かれる。
r は回路の微小要素 ds からPまでの距離で,θ は ds と r とのなす角。磁場の向きは電流の進む向きに右ねじを回すときのねじの回転方向になる。電流がつくる磁場については,ビオ=サバールの法則のほかにアンペールの法則もあるが,いずれか一方より他方が導かれる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
百科事典マイペディア
「ビオ‐サバールの法則」の意味・わかりやすい解説
ビオ=サバールの法則【ビオサバールのほうそく】
定常電流のまわりに生じる磁場の強さを与える法則。電流の強さをI(アンペア)とすると,その微小な長さds(メートル)が,距離r(メートル)離れた点につくる磁場の強さdH(アンペア/メーター)は,微小部分dsと距離rのなす角をθとし,(式1)方向は距離rと微小部分dsの両方に直角である。回路全体についてベクトル的に積分すれば任意の形の電流がつくる磁場の強さが計算でき,その内容はアンペールの法則に一致する。1820年にフランスの物理学者ビオとサバール〔1791-1841〕が発見。
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
世界大百科事典(旧版)内のビオ‐サバールの法則の言及
【渦】より
…この速度の大きさvと円周2πrとの積γ=2πrvは1本の渦糸に沿ってはどこでも一定であって,このγを渦糸の強さと呼ぶ。一般に渦糸から離れた任意の点での誘導速度は,γに等しい強さの電流が流れる同形の電線による磁場(ビオ=サバールの法則)と同一である。不生不滅の渦では渦がまわりの流れとともに流されていくとみなすことができる。…
※「ビオ‐サバールの法則」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
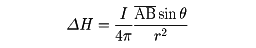

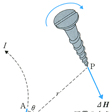


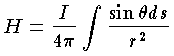 r は回路の微小要素 ds からPまでの距離で,θ は ds と r とのなす角。磁場の向きは電流の進む向きに右ねじを回すときのねじの回転方向になる。電流がつくる磁場については,ビオ=サバールの法則のほかに
r は回路の微小要素 ds からPまでの距離で,θ は ds と r とのなす角。磁場の向きは電流の進む向きに右ねじを回すときのねじの回転方向になる。電流がつくる磁場については,ビオ=サバールの法則のほかに