一般解（読み）イッパンカイ（英語表記）general solution

デジタル大辞泉

いっぱん‐かい【一般解】

n階の微分方程式について、n個の積分定数を含む関数として表された解。

出典　小学館

ブリタニカ国際大百科事典 小項目事典

一般解
いっぱんかい
general solution

一般に解が一意的に定まらない場合，特に微分方程式の解に関して多く用いられるが，三角方程式や連立1次方程式の解についても使うことがある。 (1) 最も簡単な微分方程式 y'＝f(x) の解の全体は，
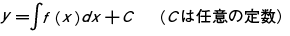で与えられる。これと同様に，1階の常微分方程式の一般の場合にも，1つの任意定数を含む解が得られ，1つの解としては定まらない。このような解を微分方程式の一般解という。一般に，n 階の常微分方程式では n 個の独立な任意定数を含む解をその一般解と呼ぶ。この一般解は曲線の集合をつくる。ここで n 個の独立な任意定数とは，n－1 個以下の任意定数では，同じ曲線の集合を表わせないような，任意定数の1組を意味する。 (2) 1階の偏微分方程式 F(x，y，u，∂u/∂x，∂u/∂y)＝0 を考える。ここで x ，y は独立変数，u は未知関数，∂u/∂x ，∂u/∂y はそれぞれ1階の偏導関数である。この微分方程式の完全解は2つの任意定数 a ，b を含む関数族 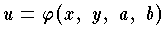の形で表わされる。この完全解から他の解も簡単に得られる。すなわち b が a のある関数 b＝ω(a) とすると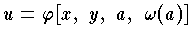， の形の曲面の集合が得られ，この全体を上の偏微分方程式の一般解と呼ぶ。 (3) 周期関数である三角関数を含んだ三角方程式の解は，求める解の値を一般解で表わす必要がある。それゆえ三角方程式 sin x＝a ， cos x＝a ， tan x＝a の解はただ1つには定まらず，それぞれ x＝nπ＋(－1)ⁿα ，x＝2nπ±α ，x＝nπ＋α ( α は方程式を満足する最小の正の角をとる。 n は任意の整数) が，与えられた方程式の解となる。個々の解は，n に特定の値を与えて得られるので，以上の解を一般解という。三角不等式についても同様である。 (4) 連立1次方程式の個数が未知数の個数より少いとき，または係数行列の階数が低下しているときには，その解は一意的でなく，いくつかの助変数を含む1次式で与えられ，助変数の値を定めるごとに個々の解が得られる。これを与えられた連立1次方程式の一般解という。以上の4つの例において，任意定数，n ，c にある特定の値を与えて得られる解を，それらの方程式の特殊解という。

出典　ブリタニカ国際大百科事典 小項目事典