二次方程式（読み）にじほうていしき（英語表記）quadratic equation

精選版 日本国語大辞典

にじ‐ほうていしき‥ハウテイシキ【二次方程式】

1. 〘 名詞 〙 二次の代数方程式。すなわち、ax²+bx+c=0(a0) という形の方程式。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

二次方程式 (にじほうていしき)
quadratic equation

方程式ax²＋bx＋c＝0（a，b，cは定数でa≠0）を二次方程式といい，この方程式を満たすxの値をこの方程式の根，または解という。

　二次式ax²＋bx＋cの因数分解がわかるときには，それから根が求まる。つまりax²＋bx＋c＝（a₁x＋c₁）（a₂x＋c₂）と因数分解されれば，－\(\frac{c1}{a1}\)，－\(\frac{c2}{a2}\)が根である。またαが根である場合には（x－α）でax²＋bx＋cを割ることで因数分解が求まり，したがって，もう一つの根が求まる。a，b，cが整数の場合に，\(\frac{n}{m}\)（既約分数）が根となりうるのは，mがaの約数であり，nがcの約数（負の約数も含める）である場合に限られる。

　D＝b²－4acを上の二次方程式の判別式discriminantという。これを用いると二次方程式の2根は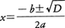，で与えられる。D≠0のときには，二次方程式は相異なる2根をもち，D＝0のときには上の式で与えられる2根は一致し，2重根となる。上の方程式の2根をα，βとすると（2重根のときにはα＝β），次の根（解）と係数の関係が得られる。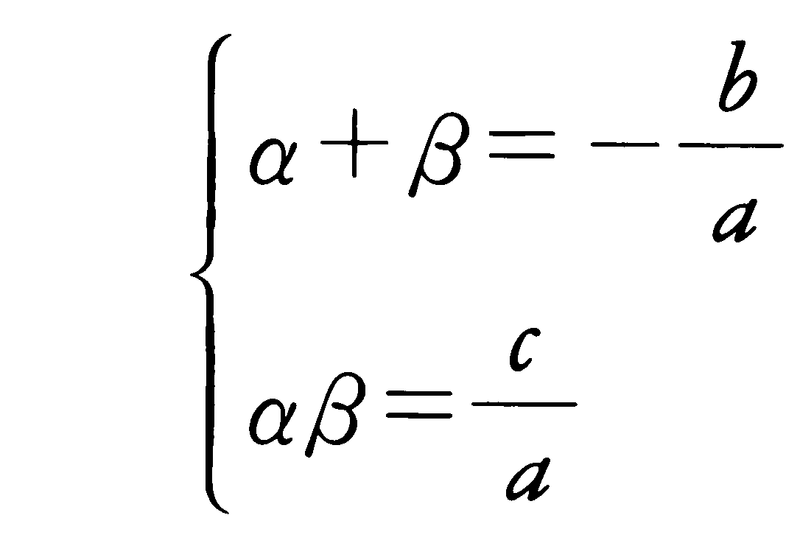

また，このときD＝a²（α－β）²となっている。

　以下，a，b，cが実数のときを考える。このとき，Dは実数だから，D＞0，D＝0，D＜0の三つの場合が考えられ，それぞれの場合に応じて，2根α，βは次のようになる。

　（1）D＞0のときには，

　　α，βは相異なる実数　……（2実根）　

　（2）D＝0のときには，

　　α＝βで実数　……（2重根）　

　（3）D＜0のときには，

　　α，βは相異なる虚数　……（2虚根）　

この三つの場合に，二次関数y＝ax²＋bx＋cのグラフは，それぞれ図のようになっている。

　次にD＞0の場合を考えよう。このとき，α，βは異なる実数だからα＜βと仮定すると，α，βと0の関係として次の三つが考えられる。0＜α＜β（α，βは正），α＜0＜β（αは負，βは正），α＜β＜0（α，βは負）。これらの三つの条件は，根と係数の関係を用いて，係数a，b，cの条件でいいかえることができる。すなわち，次のようになる。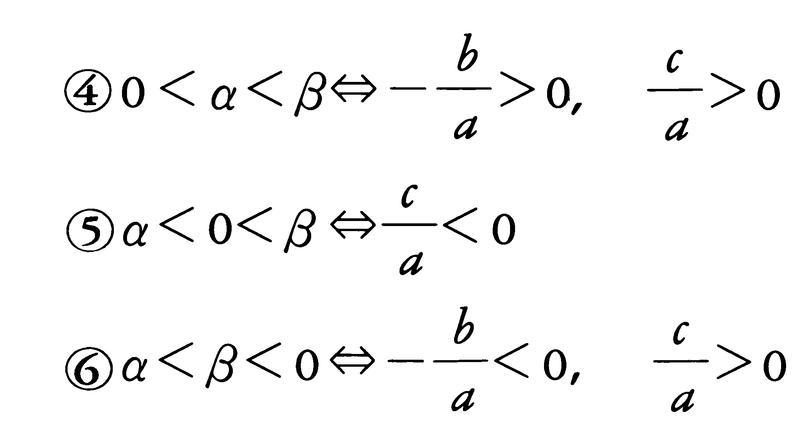

この三つの場合に応じて，y＝ax²＋bx＋cのグラフは図のようになる。
執筆者：斎藤 裕

図－二次方程式

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

2次方程式
にじほうていしき
quadratic equation

1つの未知数 x の方程式において，x の最高次数が2次であるとき，この方程式を2次方程式という。すなわち ax²＋bx＋c＝0 の形の方程式をいう。ここに a ，b ，c は定数で，a≠0 である。上の2次方程式の根は，2個存在し，
で与えられる。また根の存在は，判別式といわれる D＝b²－4ac の値によって次のように定まる。 (1) D＞0 のときは，相異なる2つの実根，(2) D＝0 のときは，ただ1つの実根 (実は 2 つの等しい根で重根といわれる) ，(3) D＜0 のときは，相異なる2つの虚根 (実根はない) が存在する。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

二次方程式【にじほうていしき】

二次関数を０に等しいとおいて得られる方程式。一元二次方程式はax²＋bx＋c＝０（a≠０）。二根は（式１）。→三次方程式／四次方程式
→関連項目ディオファントス｜方程式

出典　株式会社平凡社