上界（読み）ジョウカイ（英語表記）upper bound

デジタル大辞泉

じょう‐かい〔ジヤウ‐〕【上界】

１ 仏語。
㋐天上の世界。天上界。下界に対していう。
㋑色界と無色界。欲界に対していう。
２ 数学で、実数の集合のどの数よりも小でない数。

出典　小学館

精選版 日本国語大辞典

じょう‐かいジャウ‥【上界】

1. 〘 名詞 〙
2. ① 仏語。天上の世界。天上界。⇔下界。
   1. [初出の実例]「西方欲_レ蹈瑠璃地、上界応_レ看碼碯雲」(出典：扶桑集（995‐999頃）七・重押聞字〈橘在列〉)
   2. 「人六行観を修して上界の定を得んと思ふとき」(出典：発心集（1216頃か）七)
   3. [その他の文献]〔張九齢‐祠紫蓋山経玉泉山寺詩〕
3. ② 仏語。色界、無色界をいう。欲界（下界）に対していう語。〔諸経要集‐一一〕
4. ③ 数学で、一つの集合に属する数のどれよりも小でない数。⇔下界(かかい)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

上界 (じょうかい)
upper bound

実数からなる集合Eがあって，Eに属するどの数もある数aより大きくないとき，aはEの上界であるという。aが集合Eの上界であれば，aより大きい数はすべてEの上界である。上界が存在するときEは上に有界boundedであるという。上界が存在しなければ，Eはいくらでも大きい数を含む。上界と同様に大小関係を逆にして，下界lower boundも定義される。上界も下界も存在するとき単に有界であるという。Eの各元の符号をかえたものの集合｛－x｜x∈E｝を－Eと書くことにすると，aがEの上界であれば－aは－Eの下界である。例えば，1，\(\sqrt{2}\)などは，E＝｛1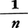－｜nは自然数｝の上界，0，－1/2などは下界であり，Eは有界である。また，－1，－\(\sqrt{2}\)などは，－E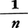＝｛－1｜nは自然数｝の下界である。
執筆者：杉江 徹

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

上界
じょうかい
upper bound

順序集合 M の部分集合，たとえば，ある実数の集合 A に対し，x∈A ならば常に x≦a となるような M の元 a が存在するとき，これを A の上界という。つまり，A のすべての元を上から押える数のことである。常に a≦x となるような M の元 a は，下界といわれる。少くとも1つの上界 (あるいは下界) をもつ A を，上に有界な (あるいは下に有界な) 集合という。 M に上界 (あるいは下界) があれば，これを最大元 (あるいは最小元) と呼び，maxM (あるいは minM ) と書く。

出典　ブリタニカ国際大百科事典 小項目事典