原子軌道関数（読み）げんしきどうかんすう（英語表記）atomic orbital

改訂新版　世界大百科事典

原子軌道関数 (げんしきどうかんすう)
atomic orbital

原子内では，個々の電子の雲（電子雲electron cloud）が重なりあって存在するとして，よく個々の電子の雲の状態は複素関数で表される。この複素関数は古典力学（ニュートン力学）における電子の円軌道，楕円軌道に相等するものなので，原子軌道関数と呼ばれ，略して原子軌道ともいう。原子軌道関数には，その広がりの程度と角運動量の大きさとに対応して，1s，2s，2pなどの名前がつけられている。水素原子の原子軌道関数は量子力学によって正確に求められる。基底状態の原子軌道関数は1s軌道関数で，これは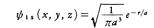，の形に表される。ただし，ここでx，y，zは原子核の位置を原点とする直交座標で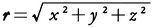，は原点からの距離，aはボーア半径である。

　水素原子以外の原子の原子軌道関数の原型は，1930年にアメリカのスレーターJohn Clarke Slater（1900-76）によって与えられた。それによると，1s軌道の関数は，

　ψ_1s（x，y，z）＝Ne⁻^ζr

という形をもつ。ただし，N，ζは定数である。｜ψ_1s（x，y，z）｜²は電子雲の密度を表し，｜ψ_1s（x，y，z）｜²dxdydzは体積dxdydzの中に電子が存在する確率を表す。これを全空間にわたって積分したものは1にならなければならないから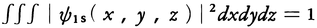，という条件がある。これを規格化の条件と呼ぶ。Nは規格化の条件を満たすように定められるので，規格化の定数と呼ばれる。ζは軌道指数と呼ばれ，ζ＝（Z－0.3）/aとされる（Zは原子番号）。0.3は他電子の負電荷が原子核の正電荷のつくる電場を打ち消す効果を表し，さえぎりの定数と呼ばれる。上記の軌道関数はスレーター軌道関数と呼ばれる。今日ではスレーター軌道関数より精度の高い軌道関数が知られている。

　二つの原子が接近して，その電子雲が互いに重なりあうと，化学結合が起こりうる。この過程で発生するエネルギーは，原子軌道関数を用いて純理論的に計算することができる。原子どうしが互いに及ぼしあう力も計算でき，また分子が形成される場合に，どのような形の分子ができるか，すなわち分子内で原子がどのように配置されるかということも理論で調べることができる。
→原子
執筆者：伊藤 敬

出典　株式会社平凡社「改訂新版　世界大百科事典」

化学辞典 第2版

原子軌道関数
ゲンシキドウカンスウ
atomic orbital function

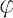原子に対する軌道関数で，水素類似原子以外では一体近似にもとづく近似解として得られる．しかし，その形は水素類似原子と同様に，動径rに依存する部分と角度θ，に依存する部分の積として，

ψ_nlm(r,θ,) ＝ R_nl(r)Y_lm(θ,φ)

のように表され，Y_lm は水素類似原子の場合と同じく球面調和関数である．R_nl は変分法にもとづいて決定される．原子軌道関数は，主量子数n，方位量子数l，磁気量子数mによって指定され，これらはn ＝ 1，2，3，…；l ＝ 0，1，2，…，n － 1；m ＝ 0，±1，±2，…，±lの値をとりうる．エネルギーは，通常，nとlを指定することにより定まるので，nの値およびl ＝ 0，1，2，3，…に対するs，p，d，f，…の記号を用いて，原子軌道エネルギー準位を1s，2s，2p，3d，…などのように表す．

出典　森北出版「化学辞典（第2版）」

世界大百科事典（旧版）内の原子軌道関数の言及

【原子】より

…また，エネルギーの高い状態では電子が陽子から遠くにあるという共通点もある。このような両者の類似点に着目して，1s,2s,2pなどの状態の波動関数を原子軌道関数と呼ぶことが多い。また，さらに省略して単に軌道と呼ぶこともある。…

※「原子軌道関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」