化学結合（読み）カガクケツゴウ（英語表記）chemical bond

デジタル大辞泉

かがく‐けつごう〔クワガクケツガフ〕【化学結合】

分子内での原子間の結びつき。その機構によって、共有結合・イオン結合・配位結合・金属結合などがある。

出典　小学館

精選版 日本国語大辞典

かがく‐けつごうクヮガクケツガフ【化学結合】

1. 〘 名詞 〙 分子内での原子間の結びつき。結合様式によって、共有結合、イオン結合、金属結合、配位結合などがある。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

化学結合
かがくけつごう
chemical bond

概説

分子種内での原子あるいはイオンの結び付きをいう。いくつかの原子あるいはイオンが引き合って集まり、分子、多原子イオンあるいはイオンの集合体などの分子種をつくるとき、それらの原子あるいはイオンは、化学結合によって結び付いているという。たとえば、水の分子H₂Oは水素原子二つと酸素原子一つとの集合体、ヘキサシアノ鉄(Ⅱ)酸イオン[Fe(CN)₆]^4-は、鉄・炭素・窒素の原子あるいはイオンの集合した多原子イオン、塩化ナトリウムNaClの結晶は、Na⁺とCl^-のイオンが交互に三次元的に連なってできた集合体で、これらの原子あるいはイオンの結び付いている機構が化学結合である。

［中原勝儼］

化学結合の基本的認識

化学では原子を物質の構成要素と考え、化学変化は、構成要素である原子の組み替えによっておこるものであるから、化学結合は化学のもっとも基本的な問題としている。したがって古くからいろいろに論じられてきたが、20世紀に入ってからの量子力学の発展によって、しだいにその姿が明らかにされている。すなわち、化学結合は原子間の相互作用で、主としてそれぞれの原子に属する電子の相互作用によるという考えである。相互作用の様式は、結合の機構によってイオン結合（静電結合、異極結合ともいう）、共有結合（電子対結合、等極結合ともいう）、配位結合（提供結合ともいう）、金属結合などに分類されることが多い。このほか、分子間化合物の生成のもととなる水素結合や、電荷移動型結合などもある。ただし実際の化合物中にみられる結合は、これらのうちの単一なものではなく、複合したものと考えられるが、その本質としては、イオン結合と共有結合の二つを考えればよい。また結合の多重度によって単結合（一重結合）、二重結合、三重結合などと分類することもあり、結合電子の軌道によって、σ(シグマ)結合、π(パイ)結合、δ(デルタ)結合などに分けることもある。

［中原勝儼］

化学結合の概念の変遷

化学結合についての概念は、古い時代にはあまりはっきりしたものではなかった。たとえば、19世紀の初めごろイギリスのドルトンは、彼の原子説に基づき、原子間の結合は簡単な割合でつくられると考え、もっとも普通の化合物、たとえば水とかアンモニア、二酸化炭素などは、いずれも成分元素の原子が1対1で結合しているとした。ただしこの結合がどのような原因によって生ずるか、またどうして1対1になるかも明らかにしていないが、これがいわゆる共有結合の最初の概念かもしれない。しかしこの考え方からは、当量や原子価の概念は当然生まれてこなかったし、アボガドロの分子、原子の概念によって否定されることになった。

［中原勝儼］

電気化学的二元説――化学結合研究の端緒

1800年イタリアのボルタが電池を発明したが、電池によって水を電気分解し、酸素と水素とにすることができるのがわかり、さらにイギリスのH・デービーが1807年、固体の水酸化カリウムや水酸化ナトリウムを電気分解して金属カリウムや金属ナトリウムを取り出すことに成功した。デービーはこれを説明するため、すべての無機化合物は、陽電気を帯びた原子と陰電気を帯びた原子とが互いに引き合ってできると考えた。これが現在でいうイオン結合のもっとも古い概念であろう。1810年スウェーデンのベルツェリウスはこの考えを拡張し、正と負の二つの原子または原子団が電気的に引き合って化合物をつくると考えた。これをベルツェリウスの電気化学的二元説といっている。この考え方は無機化合物をうまく説明できたので広く行き渡り、ドイツのウェーラーがシアン酸アンモニウムから尿素を合成することに成功し、無機化合物と有機化合物との間に本質的な差異のないことを明らかにしたので、この二元説によって有機化合物まで説明することが考えられた。しかしフランスのデュマは1834年、多くの有機化合物中のHをClに置換できるのに着目し、二元説のとおりに有機化合物の分子が正と負の部分からなるとすれば、電気的にいって正のHと負のClは置換できないとして、その矛盾を指摘した。デュマの弟子ローランの、有機化合物には一定の核があるという説を経て、フランスのジェラール（ゲルアルト）による、有機化合物の複分解から得られる結論としての型の説によって有機化合物は分類、整理され、ますます二元説の矛盾が明らかになった。

［中原勝儼］

原子価説の登場――電気化学的二元説の後退

ジェラール（ゲルアルト）は型の説から出発し、すべての化合物は2個の基からなり、H₂あるいはHClの置換体とみなせると考え、さらにはそれらの複合型、混合型までも考え、基本型は水素型、塩化水素型、水型、アンモニア型の四つであるとした。図Aにみるように、各元素の原子には一定の結合能力があることになる。このことをはっきりと指摘したのはドイツのケクレで、彼は1857年この結合能力のことをBasizitätまたはAtomigkeitとよび、HおよびClを一原子性、Oを二原子性、Nを三原子性などとよんだ。これに対し、その名称が誤解を招きやすいということから、ケクレの弟子ウィヘルハウスCarl Hermann Wichelhaus（1842―1927）はAtomigkeitのかわりにValenz（原子価）という語を提案し、これが一般的に用いられるようになった。すなわちHおよびClの原子価は1価、Oは2価、Nは3価となる。この原子価の考え方はケクレ以外にもあり、1852年イギリスのフランクランドは、無機化合物の化学式から、元素には一定の結合能力があることを示したし、1855年イギリスのオドリングも、各元素には一定の置換能力があることを示し、H′、Cl′、O″、S″などの記号を使っている。その意味では原子価の概念の創始者はフランクランドであるともいえる。

　ケクレはさらに、メタンの分子式がCH₄であると主張し（そのころ炭素の原子量は6であるとされ、メタンの分子式はC₂H₄と書かれていたが、のちジェラールの型の説から原子量の概念がはっきりとしC＝12となった）、ジェラールの四つの基本型のほかに新たにメタン型を追加し、1価原子なら四つ、2価原子なら二つの相手と結合することを明らかにした（図Aの(5)）。

　ここで初めて、原子量／当量＝原子価という関係が明らかになったが、ケクレはさらに、メタンのHをCH₃、C₂H₅などで置換すると各種の誘導体ができることから、炭素原子どうしの結合のあることをみいだし、ついで有機化合物の鎖状構造を考えるに至った。ケクレはこれに図式的な記号を用い、図Bのように、原子価数に応じて円または団子形で表した（しかし、この方法を普段使うのはきわめて繁雑であったのでケクレはさらに改良を加え、この団子形の記号をやめ、原子記号の周りに円を描き、これに原子価の数に相当する線を引いてその結合を表したが、1866年フランクランドはその円も省略して現在用いられている構造式を提案した）。

　その後ケクレは1865年、解決のむずかしかったベンゼンの構造式を、有名なケクレ式を用いることで説明し、炭素化合物のすべての構造式を解決した。

　ケクレは、原子価は原子の基本的性質で、原子量と同じく一定不変のものであるとし、有機化合物ばかりではなく、無機化合物にも適用できるものと考えた。これに対して、原子価概念の創始者ともいうべきフランクランドは、初めに無機化合物の構造式を考え、原子価の概念に到達し、各元素は、2種またはそれ以上の一定の結合能力をもつことを主張した。たとえば、ケクレは、窒素やリンは3価のみであると信じ、NH₄ClやPCl₅は、NH₃とHCl、PCl₃とCl₂との分子化合物であると考えたが、フランクランドはNやPでは原子価3と5があるのだと考えていた。これらの考え方は、いずれにしても構造的には単純な有機化合物の結合を整理するのに便利であったため大いに用いられ、有機化学発展の原因の一つとなったが、その成果の大きいことに眩惑(げんわく)され、各種の構造形式のある無機化合物にまで適用したことから、かえって無機化学の発展を誤らしめたといえる。この解決は、その後かなり時間がたってからスイスのA・ウェルナーによってなされるのである。

［中原勝儼］

原子価説の発展――四面体原子価説と、配位理論による補強

ケクレの炭素の4価の考えをさらに確実にしたのは、1874年、独立に発表されたオランダのファント・ホッフとフランスのル・ベルの四面体原子価説であって、その後の有機立体化学を開くことになる。

　彼らは、そのころまでに知られていた酒石酸や乳酸などの光学活性を説明するため、不斉炭素の概念を取り入れ、四面体原子価を証明した。この四面体炭素はそれ以外にも有機化合物の異性体の生成をも説明することになり、ここに古典的原子価説は完成された。しかし、これを無機化合物に適用すると、当時、分子性の化合物といわれるものについては、フランクランドの原子価説では満足すべき説明は得られなかった。この問題は、当時きわめて特殊な化合物とみられていたいわゆる錯塩の構造研究によって解決された。そのころ知られていたコバルト錯塩は、すべて各種の美しい色をもっており、ルテオ塩CoCl₃・6NH₃（黄褐色）、プルプレオ塩CoCl₃・5NH₃（赤紫色）、ロゼオ塩CoCl₃・5NH₃・H₂O（バラ色）、プラセオ塩（緑色）およびビオレオ塩（紫色）CoCl₃・4NH₃などとよばれていた。これらの化合物のうち、多数のNH₃がどのような位置を占めるのかきわめてむずかしい問題であり、有機化合物の-CH₂-CH₂-CH₂-…などのような鎖状構造と同じようで、五価窒素の-NH₃-NH₃-NH₃-…の鎖状構造が考えられていたが、異性体を説明することができなかった。これを巧みに説明する画期的な考え方を提出したのがウェルナーで、1893年、配位理論によってこの問題を解決した（図C）。彼は、原子価には主原子価と側原子価があり、CoとClの間は主原子価、分子で結合の飽和しているNH₃やH₂OとCoとの間は側原子価で結ばれると考え、正八面体の中心にCo原子があり、六つの頂点にはNH₃あるいはClなどがあるとした。このように考えるとCoCl₃・4NH₃にビオレオ塩とプラセオ塩の2種の異性体が存在することを容易に説明できることがわかった。八面体型6配位のほかに四面体型4配位構造、正方形型4配位構造の場合も考え、無機化合物の結合についての説明に成功した。またこの配位構造から無機化合物の異性現象を説明することが可能になり、無機化合物にも光学異性体の存在することを証明した。

　以上のフランクランドおよびケクレの原子価による結合、ウェルナーの主原子価および側原子価による結合の概念は、彼らの科学的直観から出たもので、それらの原因となる電子は、そのころまだ発見されていなかったのである。

［中原勝儼］

電子の発見と二元説の再構築

ベルツェリウスの二元説は、原子価説に押されて影が薄くなったが、1887年スウェーデンのアレニウスの電離説の発表以来ふたたび勢いを増した。イギリスのJ・J・トムソンが1897年電子を発見し、それに基づいて1904年原子模型を組み立てたのに伴い、原子構造を理論的背景として、化学結合理論の第一線に再登場してくる。

　19世紀の末イギリスのW・ラムゼーにより希ガス元素が発見され、これが原子構造を考えるうえでの基礎となったが、J・J・トムソンは最初の原子模型を考え、これと希ガス元素の不活性とを結び付け、原子間の静電的結合について説明した。彼は、原子はもっとも安定な電子配列をとろうとし、希ガス元素は電子配列が安定なので化学的に不活性であるが、他の元素の原子はいくつかの電子を得るか、あるいは失って希ガス構造をとり、そのため陽イオンあるいは陰イオンを生成して、それらの間に結合を生ずると考えた。たとえば、NaおよびMgは、電子をそれぞれ1個および2個失ってネオン型の配列となり、OおよびFは電子をそれぞれ2個および1個得てネオン型となり、それぞれNa⁺、Mg²⁺、O^2-、F^-などとなって、1価および2価陽イオン、2価および1価陰イオンとなり、NaF、MgOのようになる。これまで、単に陽性元素とか陰性元素とかいわれてきたものが、なぜ陽性や陰性になるのかが電子によって初めて説明されたわけである。

　周期表では各周期の初めのほうの元素は電子を失って陽イオンとなりやすい陽性元素であり、各周期の終わりのほうの元素は電子を得て陰イオンとなりやすい陰性元素である。1904年ドイツのアベックRichard Abegg（1869―1910）は、この考えから周期律と原子価との関係を取り扱い、陽性元素が陽イオン、陰性元素が陰イオンとなって結合するときの原子価を正常原子価と名づけ、その逆の場合を逆原子価と名づけて、それらの最高絶対値の和はつねに8になることを示した（アベックの規則）。

　この正負の原子価の概念は普通の分子にも適用され、1908年イギリスのフレンドは自由原子価ということばを提案。水素を基準とし、水素はつねに正の1価とし、それと結合するものは負の自由原子価とした。正の自由原子価は、水素を基準にして得た酸素が負の2価であることから決められる。

　このころ、ようやくデンマークのN・H・D・ボーアの原子模型が発表され（1913）、ゾンマーフェルトが改良を加えて精密な理論にまとめあげ、化学結合を電子によって説明できることがはっきりしてきた。1916年ドイツのW・コッセルは、化学結合を静電気的に説明する考え方を発表した。彼はJ・J・トムソンの考えを明確にし、またアベックの規則も含め、各元素は希ガス元素を中心として周期表上の位置に対応した正負の原子価で結合し、このような化合物はすべて異極性化合物であるとした。この考えは静電原子価の概念を明確にしたが、二元説である限り等極結合（共有結合）の説明をすることができなかった。

［中原勝儼］

電子的原子価理論と八隅子理論

コッセルの原子価理論が発表されたのと同じ年の1916年、アメリカのG・N・ルイスは、初めて等極結合を説明する電子的原子価理論を発表した。彼は、原子やイオンだけではなく、分子内でも同じように各原子は希ガス元素の原子の電子構造が安定であると考え、原子間の結合は、原子の最外側にある電子が原子間に共有され、希ガスと同じ電子構造になるために生じるとした。電子を点で表すと、水素は1電子をもっているので、H・＋・H＝H：Hのように、1対の電子を共有すると、希ガスのヘリウムと同じ電子構造になるし、炭素は最外側に4個、塩素は最外側に7個の電子をもっているので、図Dの(1)のように電子対を共有して結合し、いずれも最外殻に8個の電子を含んだ希ガス原子と同じ電子配置（CはNe、ClはArと同じ）となって安定な分子をつくるとした。このときの共有された電子2個を表す点二つは構造式で示される棒一つに相当し、(2)のようになる。この考えは、これまで困難であった等極結合の説明を解決しており広く受け入れられたが、1919年アメリカのラングミュアは、さらに拡張して八隅子理論octet theoryを発表した。最外殻の電子、すなわち原子価電子の数は各元素によって異なるが、希ガスのような8個がもっとも安定である。彼は、この8電子が立方体の八つの隅にあると考え、このような構造を八隅子（オクテット）と名づけた。希ガス以外の元素は、周期表の族番号と同じ数の原子価電子があって、いずれも同じように立方体の隅を中心として振動している。しかし八隅子を完成するほうが安定になるので、不足している原子は集まって立方体の面あるいは稜(りょう)を共有することによって化学結合を生ずる。たとえばルイスの電子を点で表した式と対応させると図Eのようである。したがって八隅子のできていない原子は、ほかの八隅子の未完成な原子一つないし四つと、一つないし四つの電子対を共有して安定な分子となり、できた分子内の電子数が奇数なら不安定、偶数とくに八隅子を完成すると安定になる、とした。この考えは化学結合を理解するのにきわめて便利で、ルイスの点電子式とともに広く用いられ、ルイス‐ラングミュアの八隅子として普及した。しかし8という数にこだわっているため、四つ以上の結合のあるもの（たとえばSF₆など）についてはまったく説明できなかった。

［中原勝儼］

古典的原子価説の完成

このようにコッセルの静電結合（イオン結合）とルイスの共有結合によって原子価理論は大きな発展をみたが、両者をもってしても解決のつかない化合物が多くあった。それは硝酸やアンモニウム塩、あるいはいわゆる配位化合物で、これらは、1927年イギリスのシジウィックによって新しく配位結合という結合形式が導入され、初めて解決した。たとえばルイスの方法で構造式を考えると、塩化アンモニウムNH₄Clおよび硝酸HNO₃は、図Fの(1)のようにNを5価とするよりほかはなく、矛盾をきたしてしまう（Nの原子価電子の入る軌道はs軌道一つ、p軌道三つの計四つであるから四つより多くの結合はつくらない）。これに対しシジウィックは、(2)のように説明した。(a)でわかるようにアンモニア分子では、NとHの間に共有されない電子対が一つあり（これを非共有電子対という）、この非共有電子対は、原子価殻に電子対がないか不足しているイオンまたは原子と結合することができるので、たとえばH⁺とは(b)のようになる。このとき非共有電子対がH⁺に供与されて結合がつくられる。このような結合をシジウィックは配位結合といい、非共有電子対を供与するほうを供与体、電子対を受容するほうを受容体とよび、矢印をつけて、たとえば、(c)のように表した。そしてNH₄ClはNH₄⁺とCl^-のイオン結合と考えるのである。同じくHNO₃では、(d)のように示すことができる。この考え方は、各種の錯化合物についても解決することとなったので、広く受け入れられることになった。

　配位結合は、供与体D:が受容体Aに、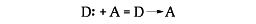

のような結合をつくるが、これを2段階に分け、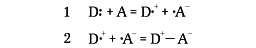

のように考えると（段階1で電子を1個D:からAに与え、段階2で結合する）、イオン結合と共有結合が一つずつあるものと考えることができる。その意味でこれをイギリスのローリーThomas Martin Lowry（1874―1936）は半極性二重結合とよんだ。

［中原勝儼］

近代的な概念

以上のように化学結合についての古典原子価論はほとんど完成したが、その本質に迫るには、1926年に誕生した波動力学の力を待たねばならなかった。それ以後現在に至るまで、イオン結合、共有結合、配位結合などについての理論的研究は進み、通常の化合物にみられる化学結合は、イオン結合性と共有結合性の混じったもので、そのいずれかの要素の強いものをイオン結合とか共有結合とよんでいるにすぎず、極端にいえば100％イオン結合性、あるいは100％共有結合性とよばれるものは少ないことなどもわかってきている。また配位結合といっても形式的にそういえるだけであって、本質的には通常の結合となんら区別されるものではない。

［中原勝儼］

化学結合の種類

化学結合の概念のうち、もっとも重要なものは、イオン結合と共有結合である。

［中原勝儼］

イオン結合

陽イオンと陰イオンとの間の静電引力に基づいてそれらのイオン間に生ずる結合をいう。典型的な例としては、塩化ナトリウムNaCl、フッ化カルシウムCaF₂などのような、陽性の強い金属と陰性の強い非金属との間にできる無機塩類にみられる。これらの化合物の結晶固体ではNa原子から電子1個が失われた陽イオンNa⁺あるいはCa原子から電子2個が失われた陽イオンCa²⁺と、ClあるいはF原子に1個の電子が付加した陰イオンCl^-あるいはF^-とが存在している。そして一つの陽イオンの周りにはいくつかの陰イオンが静電引力によって取り巻き、また陰イオンの一つ一つが静電引力によって陽イオンに取り巻かれるという形で三次元的に連なり、全体で電荷が中和されたものとなるのであって、独立したNaClやCaF₂のような分子としては存在しない（固体ではこのように存在が認められないが、気体ではたとえばNaCl分子が認められる）。このような固体は多く結晶をつくり、イオン結晶とよばれる。

　NaClの結晶は、X線構造解析によってその構造が明らかにされているが、Na⁺の周りを等距離に六つのCl^-が取り巻き、正八面体をつくっており、そのCl^-の周りに六つのNa⁺が取り巻いて正八面体をつくり、それが三次元的に連なって立方晶をつくることになる。

［中原勝儼］

格子エネルギー

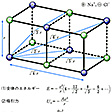
NaClの結晶を、完全に遊離したNa⁺イオンおよびCl^-イオンのみにするためには、きわめて大きなエネルギーが必要である。すなわち1413℃に熱して初めて気体となり、さらに熱して遊離イオンへの解離がみられるわけである。このことを逆にいえば、多くの遊離の陽イオンNa⁺と陰イオンCl^-とが静電引力によって集まって塩化ナトリウムの結晶をつくるときには、大きなエネルギーを放出することになる。遊離している粒子が集まって結晶をつくるときに放出するエネルギーを格子エネルギーというが、イオン結晶では、静電引力によってエネルギーの安定化を生じ、それが格子エネルギーとなっているのである。すなわちこのイオン結晶の格子エネルギーがイオン結合のエネルギーといえることになる。NaClでは陽イオンと陰イオンとの相互作用は、図Gのように一つのNa⁺を中心にして考えると、もっとも近いCl^-は距離r（この場合は2.81Å）のところに六つがある。したがって、それらとの相互作用のエネルギーは、1価イオンであることから、電荷をeで表せば－6e²/rである。次に近い距離にあるイオンのNa⁺では距離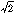rのところに12個あって、しかも同符号で反発であるから、12e²/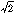rとなる。以下順次同じようにして各イオン間の相互作用のエネルギーが求められ、全体のエネルギーEは、図Gの(1)となる。（　）の中の数列は一定の値に収斂(しゅうれん)し、この場合は1.747558……となる。この値は、NaClと同じ構造をもつものならばすべて同じ値をとり、その構造に応じて決まる値で、一般にマーデルング定数といっている。したがって格子エネルギーのイオン間の引力部分U_aは、マーデルング定数をAで表せば、図G(2)となる。しかし各イオンが接近してくると、各イオンの最外側には電子が存在することから、陽イオンと陰イオンとの間であっても反発力を生じる。これは図G(3)で表される。Bはその化合物に特有な定数で反発係数といい、nはその原子の電子配置によって決まる定数である。したがって格子エネルギーUは図G(4)となる。これを実際の結晶でみられるrの値に当てはめて整理をし、Bを消去し、アボガドロ定数を掛けると、1モル当りの物質についての格子エネルギーU₀は、図G(5)という式で表される。これを実際にNaClについて計算してみるとU₀＝184kcal/molである。このように遊離イオンが集まって結晶をつくると、きわめて大きなエネルギーを放出して安定化する。

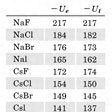
　これに対し、実際に室温でナトリウムと塩素を混ぜると反応して大きなエネルギーを発生し（生成熱ΔH₀＝－96kcal/mol）、NaCl結晶をつくる。この反応をさらに個々の反応に分けて格子エネルギーの計算ができるような経路を考えてみる。すなわち、これらの関係は図Hのようになる（このサイクルをボルン‐ハーバーのサイクルといっている）。この右辺の値はすべて実測値が知られているので、これを代入してみると、U₀（これをU_eで表す）が求められる。NaClではU_e≒182kcal/molで、先の格子エネルギーの計算値（U_tで表す）とほぼ一致する。すなわちNaClのイオン格子はほぼ100％のイオン結合であると考えてよいであろう。各種のイオン結晶についてU_eとU_tを求めてみると表のようになる。表にみられる実測値と計算値がほぼ等しいものは、イオン結合性が100％に近いものと考えることができる。しかしかなりな程度の違いがあるものは、次に説明する共有結合性が含まれているものと考えられる。

［中原勝儼］

共有結合

二つの原子が互いに電子を出し合って電子対を形成し、それを共有することによって生ずる結合をいう。一般に結合に関与している電子を点で表してH:H、Cl:Clなどのように書き、また二重結合、三重結合ではO::O、N:::Nのように表すが、さらに電子対一つを1本の線で表し、H-H、Cl-Cl、O=O、N≡Nのようにも書く。共有結合についての理論的な扱いには、主として原子価結合理論と分子軌道関数理論との二つがあるが、それらに先だってその概念を明らかにしたのは、ドイツのハイトラーとF・W・ロンドンである。

［中原勝儼］

原子価結合理論

二つの原子、たとえば二つの水素原子が無限に離れている場合、その系の全エネルギーをE₀とし、それらが接近してきたとき、E₀がどのように変化するかを調べてみる。量子力学では、その系を表すのに波動関数を用いるが、二つの水素原子とそれぞれに属する電子に番号をつけ、Aの水素原子に1という電子が、Bという水素原子に2という電子が属しているとすると、そのときこの系の波動関数ψ₁は、図Iの(1)で表される。二つの水素原子の原子核間の距離が変わるときのエネルギーの変化を計算してみると図Iのaのようになる。つまりAという水素原子に1という電子が属し、Bという水素原子に2という電子が属したまま接近してくると、距離1.7a₀のところで、約0.25eVだけ安定化した極小を生ずることになる。しかし実際に測定したポテンシャルエネルギー曲線は図Iのeで示されており、これでは実際とはほど遠い。そこでこの考え方に改良を加えてみる。一つの系内で任意の一つの電子を特定することはできないのであるから、1の電子がBに、2の電子がAに属することもできると考えて、図I(2)のような波動関数も対等に用いなければならない。すなわち、図I(3)という波動関数を近似として用いる。この関数を用いて計算すると、図Iのbのようになり、著しく改良される。このことは、遠く離れた二つの水素原子では、一方の電子は他の電子に影響を及ぼさないが、接近してくると互いに作用して二つの原子の間のどちらにも属することができ、エネルギー的に安定になるということを示している。これが共有結合（電子対結合）の本質的な部分と考えられる。電子の相互作用を原子核の電荷の効き方すなわち有効核電荷を考慮して計算するとさらに改良されて、図Iのcのようになる。ここまでの考え方は、それぞれの電子がそれぞれの原子に属する場合であるが、二つの電子が一方の原子に同時に属してしまう場合も考えてみる。たとえばH⁺(A)と:H^-(B)のようにイオンになってしまう場合である。このような状態を表す波動関数は、ψ_A(1)ψ_A(2)とψ_B(1)ψ_B(2)で、またψ_Aとψ_Bとが形では同じであるからそのどちらか一つだけをとる理由はない。したがって、図I(4)という波動関数も必要である。先のψ_covといっしょにして係数をつけると、必要な波動関数は、図I(5)となる。これを計算すると、図Iの曲線dとなり、極小値では4.10eVだけ安定化し、実測の4.72eVときわめて近くなる。このときの安定化エネルギーを結合エネルギーという。2原子が集まって結合をつくるとき、もっとも本質的な部分は、結合に用いられる二つの電子の波動関数をψ_covとしたということで、この過程を「電子を対にする」といい、この方法を原子価結合法あるいは電子対法という。またψ_covだけを考えても大部分の安定化が得られるから、水素分子内での結合は共有結合(電子対結合)が主であるといえるが、λの値は約0.2で、ψ_ionの部分すなわちイオン結合もかなり含まれていることになる。

　電子対をつくるということは、量子力学の原理から、二つの電子のスピン運動が逆方向でなければならず、このような場合スピン対をつくるというが、実際にはスピン対をつくるときにだけ電子対結合が生ずる。スピンが同じ方向のときには二つの水素原子が対をつくらないままで、安定化はおこらない。図Iの曲線fがこの場合である。

［中原勝儼］

共有結合の方向性――σ結合とπ結合

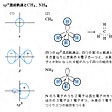
このような考え方を拡張して共有結合の方向性を説明したのはアメリカのポーリングとスレーターで、この原子価結合理論による方法を、それらの人々の名前の頭文字をとって、HLSP（Heitler-London-Slater-Pauling）法などともいっている。HLSP法では、二つの原子で、それぞれの原子の原子価電子軌道が重なり合い、その重なり合った軌道に電子対が入っているとき、共有結合を生ずると考える。すなわち、水素分子では二つの水素原子のs軌道が重なり合って、その中に一つの電子対が入り、結合をつくる。また第2周期の炭素C、窒素N、酸素O、フッ素Fなどでは、主量子数n＝2であるから、s軌道一つ、p軌道三つがあり、原子価軌道は四つある。結合に使われる軌道のこれら四つはほぼ等分に寄与するので、原子核を中心として正四面体の四つの方向に延びる四つの軌道になる。これを混成軌道といい、この場合s軌道一つ、p軌道三つからできるのでsp³混成と表す。これは図Jの(1)のような関係になる。メタンのCH₄、アンモニアNH₃を考えると(2)のようである。

　結合する相手の原子の方向を向いている軌道をσ(シグマ)軌道といい、σ軌道どうしの重なりによって生ずる結合をσ結合という。σ結合一つだけの結合を一重結合あるいは単結合という。

　結合する相手の原子数が不足のときは不飽和結合を生ずる。たとえばエチレンC₂H₄では二つの炭素原子の軌道はsp²混成をしている。そのため四つの水素原子とはσ結合をしており（図Kの(1)）、残りの一つのp軌道は、C-Cの結合方向に対して直角にあり、これらの間にπ(パイ)結合をつくっている（図Kの(2)）。このようにσ結合一つとπ結合一つの結合を二重結合という。同じくアセチレンC₂H₂ではsp混成によるσ結合と二つのπ結合によるものと説明される。このような結合を三重結合という。

　第3周期以降の元素では、s軌道、p軌道のほかにd軌道があるので、四つ以上の結合ができることになる。d軌道どうしによる結合をδ結合といい、遷移金属の化合物にはδ結合も入れて四重結合を含む化合物も多くみられる。

［中原勝儼］

分子軌道関数理論

原子価結合理論では、各原子に属する軌道が重なり合って原子が結合し、分子をつくる。これに対して、それらの理論の不備から取り扱えないとき、もっとうまく取り扱う方法として、ドイツのフントFriedrich Hund（1896―1997）とアメリカのマリケンらが発展させた方法が分子軌道関数理論で、HMH（Hund-Mulliken-Hückel）法ともいわれる。すなわち、一つ一つの分子に対しても、原子と同じ取扱いができるものと考え、分子内の各電子を波動関数ψで表し、それらは原子のときと同じようないくつかの量子数で規定され、それらの量子数が軌道のエネルギーや形を支配すると考える。このとき、多くの電子が存在する原子では、波動方程式を完全に解くのは困難で、原子核が多くある多原子分子では困難が増してくる。そのためLCAO（Linear Combination of Atomic Orbitals）近似という方法がとられる。たとえば二原子分子では、一方の核の近くで電子は主としてその核の影響下に置かれており、その波動関数はその原子の原子軌道で近似できるとして、それら二つの原子の軌道の波動関数にそれぞれ適当な係数をつけて和をとったものが、それらの分子軌道であるとする。もちろん多原子分子についても同じ方法がとられるが、これにより化学結合に関与する原子価電子のエネルギー状態を計算できる。

［中原勝儼］

配位結合

一つの原子を中心とし、その原子について方向性をもった結合を考えたとき、結合に関与する電子が形式的に一方の原子からだけ提供されている場合をいう。たとえば[Co(NH₃)₆]³⁺では、Co³⁺の周りに六つのNH₃が正八面体の六つの頂点の位置を占め、六つのNとCo³⁺との間は共有結合で結ばれている。この共有結合に関与している電子は、形式的にいえば、アンモニア分子の非共有電子対であると考えることができる。AおよびBの2原子間の配位結合は、電子を提供する原子のほうから矢印で示し、A→Bと表すこともある。

　このように配位結合とは、表面的には形式に従って分類され、命名されたもので、本質的な意味でこのような特別な結合があるものではない。多くの錯体について、その結合状態を理論的に取り扱うのにはやはり量子力学的な考え方が必要である。そのうち、純粋に静電的な立場からの取扱いには結晶場理論がある。この考え方では、錯体中の中心金属イオンに対し、周りを取り巻く配位子をすべて負の点電荷で表せると仮定し、負の点電荷が、中心金属イオンの原子価電子にどのような影響を与えるかを計算する。その結果は、純粋に静電的な結合と考えるのには矛盾があり、実際の化合物中では、かなりの共有性を認めなければならない。したがって純粋に静電的な立場の結晶場理論を修正し、共有性を取り入れることになり、その立場を配位子場理論という。また純然たる分子軌道関数理論によっても取り扱うことができ、実際ともよく一致する。したがって配位結合といっても、特別なものではなく、普通にみられる化学結合の一つで、共有結合性とイオン結合性とを含んだものということができる。

［中原勝儼］

金属結合

金属を形づくる原子間の結合をいう。金属内部のそれぞれの原子に属する原子価電子は、隣り合った特定の原子の電子と相互作用をもつことなく、結晶内を自由に運動するいわゆる自由電子となっているとみなされる。したがって、金属とは一様な密度の電子の海の中に、原子価電子を失ったその金属原子のイオンが浮かんでいるようなもので、これらの自由電子とイオンとの間の静電的な力が、全体を結合させる引力となる。これが金属結合の主要な力となるものと考えられ、このことから、金属結合は方向性をもたず、いわゆる原子価も考えにくい。しいていえば、すべて非局在化した共有性原子価結合といえる。金属結合の量子力学的な考え方としては、分子軌道関数法の立場から、ウィグナー、ザイツ、スレーターらによって説明され、またハイトラー‐ロンドンの理論の立場からは、金属原子間の共有結合に相当する多くの結合構成の共鳴によって説明されている。

［中原勝儼］

『ポーリング著、小泉正夫訳『化学結合論入門』（1968・共立出版）』▽『シェリンスキー著、大竹三郎訳『化学結合とはなにか』（1970・東京図書）』▽『M・オーチン、H・H・ジャッフェ著、中原勝儼・廣田穰訳『化学結合論――分子軌道と対称性』（1974・培風館）』▽『R・マックィーニ著、関集三・千原秀昭・鈴木啓介訳『クールソン化学結合論』上下・第3版（1983・岩波書店）』▽『小林常利著『基礎化学結合論――物質構造論入門』（1995・培風館）』▽『長谷川正著『化学結合と反応のしくみ』（1995・裳華房）』▽『志田忠正著『現代化学への入門3　化学結合』（2001・岩波書店）』▽『小島憲道・下井守編『現代物性化学の基礎――化学結合論によるアプローチ』（2003・講談社）』▽『ジャック・バレット著、吉沢一成訳『化学結合の基礎』（2004・化学同人）』

[参照項目] | アベックの規則 | イオン結晶 | 塩化ナトリウム型構造 | ベンゼン

化合物の型の説〔図A〕

炭素原子の結合〔図B〕

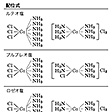
コバルト錯塩の構造〔図C〕

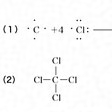
炭素と塩素の結合〔図D〕

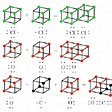
八隅子とルイスの点電子式〔図E〕

配位結合の結合形式〔図F〕

格子エネルギー〔図G〕

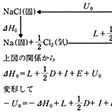
ボルン‐ハーバーのサイクル〔図H〕

格子エネルギーの理論値と実測値〔表〕

水素分子のポテンシャルエネルギー曲線〔…

共有結合の方向性〔図J〕

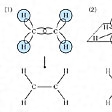
σ結合とπ結合〔図K〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

化学結合 (かがくけつごう)
chemical bond

分子の中でそれを構成する原子を互いに結びつけ，分子の形を維持しているのが化学結合である。希ガス元素（ヘリウムHe，ネオンNe，アルゴンArなど）の原子を除くと，一般の元素の原子は常温・常圧では単独で存在するよりも，他の同種または異種の原子いくつかとかなり強い力で引き合って集合して，分子を形成したほうがエネルギーが低くなり安定である。このように分子の中で強い力を及ぼし合っている原子の間には化学結合があるという。たとえば水の分子H₂Oは2個の水素原子Hと1個の酸素原子Oが結びついたもので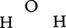，のような形をしている。これらの原子がとくに強く引き合って1個の分子を形成していることをあらわに表すために，化学結合を模式的に実線で結んで表し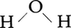，またはH－O－Hのように記す。ちなみに水分子のH－O間隔，すなわち結合距離は95.8pm（1pm＝10⁻¹²m＝10⁻¹⁰cm＝0.01Å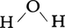），のなす角（Oの結合角）は104.45度である。このように化学結合の概念は分子概念と密接な関係にあり，分子概念が拡大されると必然的に化学結合の概念も拡大される。上に述べたのは最も基本的な意味での化学結合である。

　元来，化学では原子を物質の構成要素とみなし，化学変化を原子の組換え，すなわち化学結合の組換えの問題としてとらえてきた。したがって，化学結合の問題は化学にとっては基本的に重要であり，古くから化学者によって取り上げられ，主として化学的な事実に基づいて，原子価という立場から議論されていた。たとえば，J.J.ベルセリウスの電気的二元説（1820ころ），F.A.ケクレの炭素四原子価説（1858），J.H.ファント・ホフ，ル・ベルJoseph Achille Le Bel（1847-1930）らの炭素原子の結合の手が正四面体の中心から頂点の方向に伸びているという四面体説（1874），A.ウェルナーの配位説（1893），さらにはR.アベックの主原子価と副原子価の和が8になるという八の法則（1904）などがあり，原子には固有の原子価があることがわかってきた。19世紀末に電子が発見され，20世紀に入ってそれまで不可分とされていた原子が，原子核と電子から成ることがわかってくると，種々の原子模型が提出された。そのなかで画期的な成功を収めたものがN.H.D.ボーアの原子模型（1913）で，これに基づいてG.N.ルイスの原子価論，W.コッセルの原子価論（ともに1916）が提出され，現代の原子価概念の基礎がほぼ確立，化学結合における電子の役割が注目されるようになった。

化学結合における電子配置の役割

原子内には原子番号と同数の電子があるが，その電子は3種の量子数（n，l，m）によって規定される原子軌道atomic orbitalに，スピン量子数m_sに関する制限であるパウリの原理とフントの規則を課されて，エネルギーの低いほうから順次配置される。この原子の電子配置は，D.I.メンデレーエフやJ.L.マイヤーによって見いだされた元素の諸性質の周期性（1869）と密接に関連しており，原子の化学的性質は主としてその電子配置に支配されていることが明らかにされた。そのなかで化学結合との関係で重要なことは次の3点である。

　（1）元素の化学的性質は，関与している軌道のうちでエネルギーの高いほうの軌道にある電子（最外殻電子）の数によりおもに決まる。事実，周期表の同じ族に属する元素の最外殻電子の配置はよく似ている。（2）最外殻電子の数が8である元素は化学的にとくに安定であって，これに相当するNe，Ar，クリプトンKr，キセノンXeはHe（Heの最外殻電子は2個）とともに不活性な希ガス族を形成する。（3）最外殻電子の数が8である構造は特別なもので，一般に希ガス元素に近い電子配置をもつ元素は，電子の獲得または放出によって，希ガス元素の電子配置をとる傾向をもつ。たとえば最外殻電子が7個のハロゲンの原子は1個の電子を受け取る傾向が強く1価の陰イオンになりやすい。また最外殻電子が1個のアルカリ金属の原子は，これを放出して1価の陽イオンになる傾向が強い。II族，VI族の元素に関しても同様で，この場合は2価のイオンになりやすい。こうしてできる陰陽イオンが静電的な引力で結ばれて化学結合が成立するというのがコッセルの原子価論の骨子である。一方ルイスは，原子は最外殻電子が8個のとき最も安定になるということから出発し，最外殻電子の数が不足するときには隣り合う原子が電子を出し合って共有し，合計で8個の電子が周囲に配置されるようになると考えた。ルイスは最外殻電子を点で表し，それ以外の電子と原子核を元素記号で表して，たとえばCl₂分子やCO分子を次のように表記した。

この表記法は現在でもしばしば用いられ，ルイスの点表示と呼ばれる。I.ラングミュアはこのような考え方を八隅説，また結合を共有結合と呼んだ（1919）。ルイスの考え方の重要な点は，化学結合は原子と原子を結びつけている電子対であることを指摘したことにある。もちろん当時はこのような結合形成の機構に対して理論的な裏づけはなかったが，今日では量子力学的に裏づけられ，現在の化学結合概念を築く基礎になっている。

化学結合の種類

化学結合には電荷の偏りぐあい，強弱など種々あるが，多くの化学的な事実から帰納的に大別するとイオン結合，共有結合，金属結合が重要である。そのほかに配位結合，水素結合，電荷移動相互作用など，また電気双極子や分極に基づく相互作用もある。さらにやや特殊なものとして一電子結合がある。分子がいくつかの原子核といくつかの電子から構成されているという観点に立てば，化学結合の問題は原子核-原子核，電子-電子，原子核-電子の相互作用と電子および原子核の運動，さらに電子スピンなどの因子を含めて考慮することによって，原理的には統一的な理解に到達できるはずのものである。化学結合の性格は，これらの因子の大小関係で決まり，結合の種類に対応すると考えられる。この意味では上記の分類は便宜的なものにすぎず，現実の結合はすべてこれらの中間的な性格をもっている。イオン結合と共有結合については次節で述べるので，そのほかの結合について簡単に触れておく。

　まず金属結合は金属内の金属元素イオンを相互に結びつけている結合で，金属内をほぼ自由に動く自由電子（最外殻電子に由来する）とイオンとの静電的な引力が主要な凝集力と考えられる。金属の特性，たとえば金属光沢，熱伝導率が良いこと，電気伝導度が大きいこと，熱容量やエントロピーが大きいことなどは，この自由電子の存在に起因している。金属結合が他の結合と大きく異なる点は，結合に方向性がほとんどないことである。このことは電子が多数の原子の上を遍歴しているから当然であるが，金属が展性，延性に富むことと関連している。

　配位結合というのは，結合に当たる電子対が一方の原子からのみ供給されたもので，広義には共有結合の一種とみなせる。しかし，電子対を提供した原子は若干陽性を帯び，受け取った原子は陰性が増すので，イオン結合の性格も併せもつと考えられ，この名称が用いられる。遷移金属イオンと青酸イオン，アンモニア，有機化合物の塩基類との錯化合物の結合は代表的なもので多数の例があるが，比較的簡単な化合物にもしばしばみられる。

　水素結合は，電気陰性度の大きい窒素，酸素，フッ素などと共有結合している水素原子が，他の分子の陰性の原子との間につくる結合で，比較的弱い結合である。他の分子の塩基性が強くなると水素結合も強くなり，次に述べる電荷移動型の結合も寄与するようになるとされている。今述べたのは分子間の水素結合であるが，1分子内でも条件に合う原子があると水素結合を生ずることがある。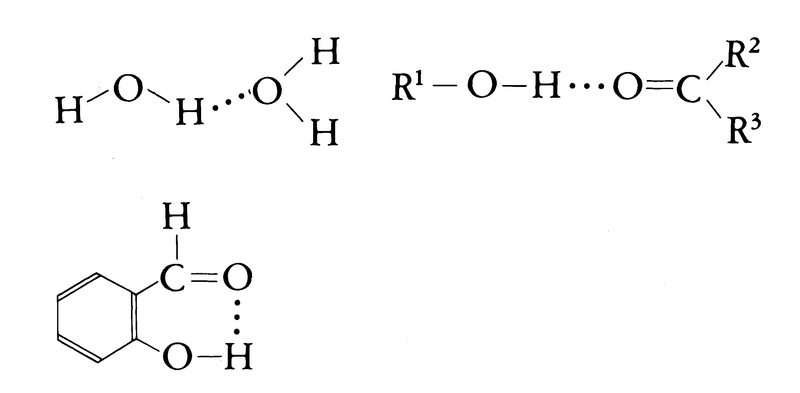

　電荷移動相互作用に基づく結合は電子供与性の化合物（Dと記す）と電子受容性の化合物（Aと記す）の間に生ずるもので，分子と分子の間の結合である。たとえば，ナフタレン，アントラセンなど芳香族炭化水素とピクリン酸やトリニトロベンゼンとの分子化合物は，両成分分子より深い色に着色することが古くから知られていた。この結合と着色の機構に対する量子論的な説明はマリケンRobert Sanderson Mulliken（1896-1986）によって与えられた（1950）。それによると，ファン・デル・ワールス力のような弱い分子間力で接しているD……Aという非結合構造と，DからAに電子が移動して共有結合が加わった電荷移動構造D⁺－A⁻との間の共鳴によるとされている。この結合が関与した化合物は有機化合物に多く知られているが，無機化合物でもたとえば混合原子価化合物でみられる。とくに有機の分子化合物で電荷移動構造の寄与が大きいものの結晶には顕著な物性を示すものが多く，有機化合物でありながら金属的な電気伝導性を示すもの（下式），さらには超伝導性や反強磁性を示すものも知られている。

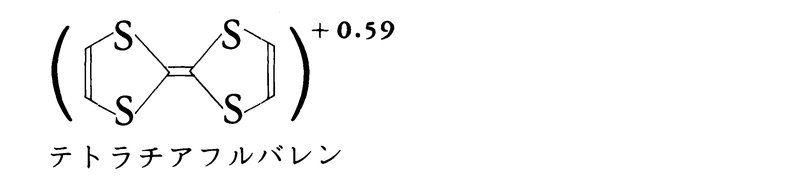
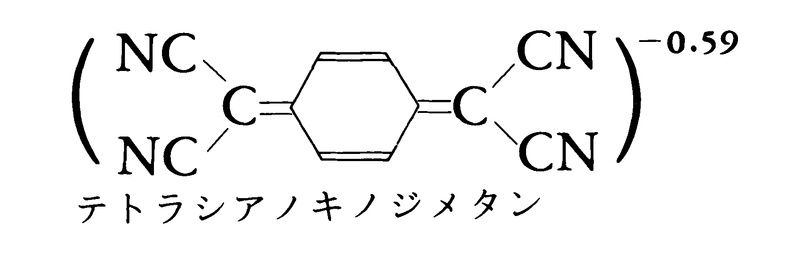
簡単な分子の化学結合

前節の初めに述べたように，化学結合の性格は種々の因子の相対的な大きさで決まる。ある分子の結合がイオン結合になるか共有結合になるかは，もとの原子が分子の平衡核間距離（結合距離）に置かれたとき，これらの因子の絡み合いでいずれの結合状態のエネルギーのほうが低くなるかによって決まるわけである。このことをみるために，簡単な3種の二原子分子NaCl，HCl，H₂の結合について考えてみる。NaClと書くと食塩の結晶を思い浮かべるが，ここではNa原子とCl原子各1個からできる気相中で安定なNaCl分子である。1mol（6.023×10²³個）のNaCl分子の結合を切ってNa原子1molをCl原子1molをつくるのに406kJのエネルギー（結合解離エネルギーと呼ぶ）が必要であることが実験によって知られている。いま，この逆の過程Na（原子）＋Cl（原子）─→NaCl（分子）でどのくらいのエネルギーが放出されるかを，結合がNa⁺イオンとCl⁻イオンのクーロン引力によってできているとして計算してみる。Na（原子）の原子核から受ける静電引力に逆らって電子を1個取り去ってNa⁺イオンをつくるのに必要なエネルギー（イオン化エネルギー）は，実験によって496kJ/molである。Cl（原子）は電子親和力が強く，この電子を受け取ってCl⁻イオンになったほうが安定で，このとき348kJ/molのエネルギーを放出する。したがってNa（原子）とCl（原子）からNa⁺イオンとCl⁻イオンを1molずつつくるのに必要なエネルギーは，（496－348）kJ＝148kJである。次にNa⁺とCl⁻がクーロン引力で近寄り，気相分子の結合距離236pm（＝2.36Å）になるが，イオンの電荷が原子核の中心にあるとしてクーロンエネルギーを計算すると588kJ/molになり，これだけのエネルギーが放出される。結局Na（原子）とCl（原子）からNaCl（分子）が1mol生成するときには（148－588）kJ＝－440kJとなり，440kJのエネルギーが放出される。いまの計算ではNa⁺とCl⁻の電子-電子反発，原子核-原子核反発のエネルギーやその他の小さいエネルギーを含めていないが，これらの補正は全体として上の数値を小さくするので，実測の406kJ/molの大部分は以上の考え方で説明される。すなわち気相のNaCl分子の結合はイオン結合ということになる。

　ところでHCl分子について同じような計算をしてみると，およそ120kJ/molとなり，実測の結合解離エネルギー431kJ/molと大きな隔りがある。また双極子モーメントの実測値も1.09D（Dはデバイで，1D＝3.3356×10⁻³⁰C・m）で，H⁺イオンとCl⁻イオンから構成されるとして予想される値の数分の1にしかならない。したがってHCl分子の結合はイオン結合とはいえず，むしろ次に述べる共有結合とされている（表参照）。水素分子H₂でもこのような計算をすることはできるが，この場合は水素原子上の電子の数が少なく核電荷の遮へい効果が小さいため，結合距離74pmでの原子核-原子核反発力が単なる補正項ではなくなって結合解離エネルギーの436kJ/molを説明できない。水素分子の形の対称性から明らかなように双極子モーメントは0Dであり電荷の偏りはなく，イオン結合と考えられない。

　水素分子はルイスの原子価論が適用できる典型的な共有結合分子の例である。水素原子の電子軌道はHeと同様2個の電子で安定な配置になるので，2個の原子が1個ずつの電子を出し合って共有することによって結合が形成される。このことを量子論を用いて定式化したのはハイトラーWalter Heitler（1904-81）とロンドンFritz London（1900-54）である（1927）。いま2個の水素原子をa，b，電子を1，2と記号づけ，水素原子aの電子軌道の波動関数をψ_aと表し，1番の電子がこの軌道にあるときψ_a（1）のように記す。そうすると電子1，2をaとbが共有している状態の波動関数ψは，ψ＝（1/\(\sqrt{2}\)）（ψ_a（1）ψ_b（2）＋ψ_a（2）ψ_b（1））のように近似することができ，この関数を用いてエネルギーを計算することによって，水素分子の結合解離エネルギーの約65%を説明することができた。現在ではもっと精密な計算ができるが，量子力学が発展しはじめた当初の計算としては大成功であり，これによって共有結合のエネルギーの本質は明らかにされたといってよいできごとであった。それは水素aの上に電子1がいてbの上に2がいる状態と，ちょうど電子を交換した状態との間の共鳴を考えたことになり，共鳴エネルギーに相当するだけエネルギーが低くなり，結合が安定化するということである。この場合の共鳴エネルギーは交換エネルギーと呼ばれている。この理論は，化学者の経験から導かれた原子価の概念や分子構造式との対応がよく，原子価結合法として発展した。

　この原子価結合法に対してもう一つの理論として，電子は分子全体に広がる軌道（分子軌道）の上を運動するとして扱う分子軌道法がその後導入された。この方法では分子軌道の波動関数φを構成原子の波動関数の一次結合で近似することが多い。水素分子の場合は先ほどのψ_a，ψ_bを用いて，φ₁＝（1/\(\sqrt{2}\)）（ψ_a＋ψ_b），φ₂＝（1/\(\sqrt{2}\)）（ψ_a－ψ_b），となる。φ₁は原子が接近するにしたがってエネルギーが減少して安定な結合性軌道になるのに対し，φ₂は逆に原子軌道のエネルギーよりもエネルギーが増加し，反結合性軌道になる。水素分子の2個の電子は，パウリの原理によりそのスピンを逆平行にしてφ₁軌道に入る。すなわち水素分子の基底状態はψ＝φ₁（1）φ₁（2）で表される。この右辺に上のφ₁を代入して展開すると，ψ＝（1/\(\sqrt{2}\)）｛（1/\(\sqrt{2}\)）（ψ_a（1）ψ_b（2）＋ψ_a（2）ψ_b（1））＋（1/\(\sqrt{2}\)）（ψ_a（1）ψ_a（2）＋ψ_b（1）ψ_b（2））｝となり，｛　｝の中の第1項は原子価結合法で得られたものと等しいが，第2項は新しく加わったものである。この第2項の中身は水素原子aの上に電子1，2がいるものとbの上に1，2がいるもの，すなわちHa⁻Hb⁺とHa⁺Hb⁻というイオン結合の分子に対応している。上の展開式をみると，共有結合を表す第1項とイオン結合を表す第2項の係数は等しく1対1の割合で寄与しているが，実際の水素分子ではイオン構造の寄与は少ないので補正が必要であり，配置間相互作用などの補正法がくふうされた。分子軌道法から得られた重要な結論は，前節および本節の初めに述べたように，共有結合とイオン結合に本質的な差異はなく，結合する原子の性質に応じて，両者の寄与の割合が異なるだけで，近似を高めれば化学結合の本質に迫れるということである。しかし伝統的なイオン結合，共有結合という分類は直観的であり，いまでも重要である。

　本節の締めくくりとして，その判定の目安について述べておく。気相で孤立した原子が電子を放出しやすいか獲得しやすいかを判定するにはイオン化エネルギーや電子親和力があるが，結合状態の原子が電子を引き寄せる能力の尺度としては，電気陰性度という尺度がL.C.ポーリング，マリケンなどによって提案されている。前者は結合エネルギー，後者はイオン化エネルギーと電子親和力に根拠を置いている。よく使われるのはポーリングの値で，原子A，Bの結合A－Bを考え，それぞれの電気陰性度をχ_A，χ_Bとすると，その差｜χ_A－χ_B｜が2より大きいとイオン結合，2より小さいと共有結合というのがおよその目安になる。表に若干の二原子分子の電気陰性度の差，双極子モーメント，結合の主要な性格を示す。電気陰性度は周期表で近隣にある元素では近い値なので，その化合物は共有結合になるが，遠く離れていると電気陰性度の差が大きく，イオン結合の化合物を与える。

複雑な分子の化学結合

イオン結晶の代表とされる食塩NaClの結晶構造はよく知られているように，Na⁺とCl⁻のイオンが前後，左右，上下の6方を相手のイオンによって囲まれた網目になっていて，特定のNaClという分子の単位を考えることができない。この場合の化学式は単に構成原子の数の比を表す）。強いて考えれば結晶全体が一つの巨大分子とみなせる。この場合の結合エネルギーは前節の気相NaCl分子の計算をいくぶん修正すれば，イオン間のクーロン力で大部分を説明することができる。修正点は注目するイオンに接しているイオンだけでなく，すべての格子点にある正負のイオンについてクーロン力を計算することである（この意味では結合はすべての格子点の方向を向いていることになる）。その結果，NaClの結晶では隣り合う1対のNa⁺とCl⁻のクーロン引力の1.7476倍になる。この数値はマーデルンク定数と呼ばれ，他の型の結晶についても計算されている。NaCl結晶ではNa⁺とCl⁻の距離が気相分子の約1.2倍になっているので，クーロン引力の正味の増加は1mol当り約1.45倍である。以上代表例としてNaClを選んだが，複雑なイオン（NH₄⁺やSO₄²⁻，さらには錯イオン）を含む無機塩類もほぼ同じように扱うことができる。そのほかイオン結晶ではイオン半径，配位数などが結合を考えるうえで重要な因子となる。

　共有結合は，同種の原子間，周期表で近接している原子間，ホウ素族，炭素族，窒素族，酸素族と水素との化合物に主としてみられる。これらは電気陰性度の差が小さいからである。とくに有機化合物は主としてC，H，N，Oで構成されるので簡単なメタンCH₄から複雑なタンパク質に至るまで，またベンゼン，ナフタレンなどの芳香族化合物をはじめとしてほとんどすべての有機化合物が共有結合でできている。これらの共有結合を考えるうえで重要なことは，混成軌道という概念である。炭素原子を例にとると，その最外殻電子の配置は (2s)² (2p)²でs軌道は球状，3個のp軌道は直交三軸の方向に亜鈴形に伸びる（図2参照）。一方メタンの分子では炭素の結合の手はファント・ホフらが指摘したように，正四面体の中心から頂点の方向に伸び，H－C－Hの結合角は109.5度である。一方ベンゼンC₆H₆は平面状の正六角形で炭素原子の結合角は120度である。さらにアセチレンC₂H₂の分子は直線状で結合角は180度である。このような結合の方向性は，s軌道とp軌道を別々に考えていたのでは説明できず，両者を混ぜ合わせることによってはじめて可能になる。詳しくは省略するが，s軌道1個と3個のp軌道を混ぜることにより正四面体角の方向の軌道を4個つくることができ，そのおのおのに電子を1個ずつ割りふると，各方向に結合する水素原子からの電子を1個ずつ加えて4本の共有結合が完成され，CH₄分子ができる。このような軌道を混成軌道と呼び，今の場合はsp³軌道と記す（図3参照）。こうしてできた結合は結合軸のまわりに対称的になり，σ結合と呼ばれる。ベンゼンの場合は，s軌道と2個のp軌道から平面内に120度の角をなして伸びるsp²軌道を3個つくることができ，残ったp軌道はこの面に垂直方向に伸びることになり，おのおのに1個ずつの電子を収容する。sp²軌道は両隣の炭素原子のsp²軌道と電子を共有してσ結合をつくり，六角形を完成する。六角形の外向きに出ている残りのsp²軌道は水素原子の1s軌道とσ結合をつくる。最後に残ったp軌道は六角形の面を節面として図4のように配列され，両隣のp軌道と結合をつくる。このように節面のある結合はπ結合と呼ばれ，そこにいる電子をπ電子と呼ぶ。p軌道には1個の電子しかないので，結合が電子対から成るという考え方では図4のエチレンの場合はよいがベンゼンのように両隣がある場合には考えにくい。この場合は二つのケクレ構造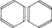間の共鳴を考えればいちおう納得できる。しかし分子軌道法の立場からは，6個の炭素原子のp軌道の一次結合をとることによって3個ずつの結合性軌道と反結合性軌道ができるので，前者に2個ずつの電子を入れると考えればよく，非常にすっきりする。このような分子軌道をπ軌道と呼び，共役二重結合をもつ分子に特有のものである。分子軌道法はこのような分子を扱ううえで有力な方法とされ，その電子的な諸性質を理解するうえで，分子軌道法が果たした役割は非常に大きい。アセチレンの場合はsp混成軌道をつくると結合の直線性が説明できる。この場合は直交した2個のp軌道が残り，それぞれ相手の炭素原子のp軌道と2個のπ結合をつくるので，σ結合と合わせて三重結合になる。共有結合に関しては有機化合物の例だけを挙げたが，無機化合物でも水H₂O，アンモニアNH₃をはじめダイヤモンド，シリコン，ゲルマニウムなど共有結合の化合物はたくさん知られている。共有結合に関しても関連する重要な事柄が多く，結合距離，結合角などのほかに，電子密度，結合次数，非局在化エネルギー，結合モーメント，非結合電子対などが挙げられる。さらに最近では化学構造式のうえでは直接結合していない原子間にもかなりの相互作用がある場合が知られており，このようなものも結合と考える必要に迫られている。

特殊な分子の化学結合

水素の気流中で放電を起こすとH₂⁺という化学種が生成する。これは1電子で2個のプロトン（陽子）を結合しているので一電子結合の分子である。原子価結合ではH・H⁺とH⁺・Hの共鳴と考えて結合エネルギーが説明され，分子軌道法の立場ではH₂分子のところで述べた結合性の軌道φ₁に電子が1個入っているとして説明される。Li₂⁺，Na₂⁺なども一電子結合の例である。またHe₂⁺，NOなどは三電子結合として説明されている。希ガス元素は不活性で他の原子と分子をつくらないとされているが，XePtF₆，XeF₂，KrF₂などが知られている。XeF₂は直線状でF⁻Xe⁺FとFXe⁺F⁻の共鳴と考えるのがよさそうである。XePtF₆はXe⁺PtF₆⁻のイオン結合とされている。この化合物は，O₂⁺PtF₆⁻がイオン結合であり，O₂とXeのイオン化エネルギーがほぼ等しいことから，イオン結合になると考えて合成された。メタロセンと総称される化合物は，遷移金属元素Mのイオンとシクロペンタジエニルの陰イオン2個から成るサンドイッチ型の分子で，M(C₅H₅)₂と表される。中心金属イオンは10個の炭素原子と等価な結合をつくっている。MがFe²⁺の場合，電子のやりとりの結果Fe⁺^1・34（C₅H₅⁻^0・62)₂のような電荷分布になっている。

化学結合に関する実験

古来，化学反応，熱力学的測定によって多くの知見が蓄積されて原子価概念の成立に役立っていたが，20世紀に入るとX線回折による結晶構造解析をはじめ各種分光学が発達し，分子の電子状態の研究が盛んになってきた。おもな実験法を列挙すると，X線回折，電子線回折，紫外・可視・赤外スペクトル，双極子モーメント，磁気測定，マイクロ波分光，磁気共鳴，レーザー分光，X線および真空紫外領域の光電子分光などがある。

化学結合の生成過程

以上，化学結合を主として結合エネルギーという静的な観点からみてきたが，そこでは分子の形はある程度与えられたものとして扱われており，化学結合が形成されていく動的な過程の側面が欠けている。この過程を実験でとらえるのは容易でないが，簡単な分子については理論的に詳しく調べられている。ヘルマン=ファインマンの静電定理で理解することが提案されている。これは，原子が互いに近づくとき，負に帯電した電子雲から原子核が受ける静電力と原子核どうしの静電力を，ある条件のもとで正確に表すものである。ここでは2個の水素原子が接近するときの電子雲のひずみの計算結果を図5に示す。図5で実線は孤立原子と比べて電子雲が増加した状態，点線は減少した状態を表している。原子が遠く離れているとき，ファン・デル・ワールス力によって電子雲は分極し原子間で増加している。この結果，原子核は電子雲に引っ張られてしだいに近づいていく。図5で示した6.0 a.u.（核間距離。1 a.u.＝52.9pm）くらい接近すると両者の電子雲は互いに侵入して重なり合い，なお原子核を引き寄せる。3～2 a.u.になると点線領域から核間の共通領域へ電子雲が流れ込み，負の電荷が増してますます核を引き寄せるようになり，これにより結合が形成されていく。これは共有結合の概念とよく対応している。図5で2a.u.以下になると，今度は原子核の外側にも実線領域が現れ，核の進行を妨げはじめ，核間反発とともに核を平衡核間距離（1.4a.u.）のところで停止させることになる。
→イオン結合　→共有結合
執筆者：木下 實

図1～図4

図5－水素分子の生成反応過程における電…

表－二原子分子の電気陰性度の差と結合の…

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

化学結合【かがくけつごう】

分子内での原子あるいはイオン間の結びつきをいう。主にイオン結合，共有結合，配位結合，金属結合に分類されるが，そのほか水素結合や，電荷移動によって生ずる結合などもある。なお化学結合の多重度によって一重結合（単結合），二重結合，三重結合などと呼ぶこともあり，また結合に用いられている電子の軌道によってσ結合，π結合，δ結合などと呼ぶこともある。ただし，実際の化学結合においては，いくつかの結合が重なりあっている場合も多い。
→関連項目化合｜結合エネルギー｜結晶構造

出典　株式会社平凡社

化学辞典 第2版

化学結合
カガクケツゴウ
chemical bond

物質の構成単位となる分子や結晶のような，原子集団中の原子の結びつきのこと．原子間の結びつきは普通，線で示され，結合または結合手とよばれる．結合している原子間の距離，結合エネルギー，結合の極性，結合角(2本の結合のなす角)などは多くの場合，実験的に知ることができる．普通に化学結合は共有結合，配位結合，イオン結合，金属結合の四つに分類されるが，配位結合は本質的には共有結合の一種とみなしてこれを除き，三つに分類することもある．厳密には，共有結合は同種原子間に形成される等極結合である．異種原子間の結合は極性を有し，共有結合とイオン結合のまじったものとして説明される．たとえば，HClの結合は電子が塩素原子のほうに偏って極性を有するが，これは共有結合性が83％ でイオン結合性が17％ まじったものと解釈されている．化学結合の分類としては，単結合，二重結合，三重結合による方法もあり，さらに価電子の軌道の種類に注目して，σ結合，π結合によって分類する方法もある．[別用語参照]原子価の理論

出典　森北出版「化学辞典（第2版）」

知恵蔵

化学結合

分子や結晶を形成する原子、またはイオン同士の結び付きで、単に結合ともいう。結合の様式は、(1)原子同士が1個ずつ出し合った電子が電子対となり、これを共有し合ってできる共有結合、(2)一方の原子の最外殻の電子が他方へ移動してイオンが生成され、電気的引力により結合するイオン結合、(3)金属原子が価電子を放出し、生じた陽イオンが規則正しく配列、その間を価電子が自由電子として動き回り全体の陽イオンを結び付ける金属結合、(4)一方の原子が持つ電子対が、他方の原子の空の軌道にも分布を広げる配位結合に分類される。実際の化学結合はこれらが混ざり合った、共鳴という現象として説明される場合も多い。中性分子の間にも遠距離まではたらく弱い引力があり、分子間力(ファンデルワールス力)という。水素原子より電気的に陰性な原子のハロゲン、窒素、酸素、リン、硫黄などが水素原子を介して弱く結び付く水素結合を広義の化学結合に含める場合もある。

(市村禎二郎 東京工業大学教授 ／ 2007年)

出典　(株)朝日新聞出版発行「知恵蔵」

ブリタニカ国際大百科事典 小項目事典

化学結合
かがくけつごう
chemical bond

原子と原子の結びつき。結びつきの仕組みにより，イオン結合，共有結合，金属結合に大別されるが，実際にはそれらの中間的なものが多い。

出典　ブリタニカ国際大百科事典 小項目事典

栄養・生化学辞典

化学結合

　共有結合，イオン結合，金属結合など，原子やイオンの間の結合．この結合によって分子や結晶が形成される．

出典　朝倉書店

世界大百科事典（旧版）内の化学結合の言及

【力】より

…その結果，分子全体としてのエネルギーがばらばらの2原子のときより低い結合状態が実現する。これが化学結合である。このときの結合エネルギーをクーロンエネルギーから生ずる部分とそれ以外の部分にわけると，交換エネルギーと呼ばれる後者のほうがはるかに大きく，それが結合エネルギーの大部分を占めている。…

※「化学結合」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」