精選版 日本国語大辞典 「毛管現象」の意味・読み・例文・類語
もうかん‐げんしょうモウクヮンゲンシャウ【毛管現象】
- 〘 名詞 〙 =もうさいかんげんしょう(毛細管現象)〔物理学術語和英仏独対訳字書(1888)〕
日本大百科全書(ニッポニカ) 「毛管現象」の意味・わかりやすい解説
毛管現象
もうかんげんしょう
細い管を液体の中に立てると、液体が管内を上昇して外部の液面より高くなったり、あるいは下降して低くなったりする現象。毛細管現象ともいう。この現象を最初に観察した(1490)のはレオナルド・ダ・ビンチといわれている。もっともよく知られているのは、ガラスの毛管を水中に立てたとき、水が毛管を上昇する場合である。布の一端を水に浸すと水が布を伝わって上昇するなど、実際の生活に関連した例も多い。
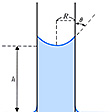
毛管現象は液体の表面張力によって生ずるもので、管壁をつくる固体との間の接触角が90度より小さく、管壁をぬらす場合には、液体は管内を上昇し、90度より大きく、管壁をぬらさない場合は下降する。毛管内の面は曲面になり、これをメニスカスとよんでいる。液面が上昇または下降するのは、このメニスカスに沿って作用する表面張力のためである。のように、半径Rの管を上昇する高さhは、表面張力をγ、接触角をθ、重力加速度をg、液体の密度をρとすると、
h=2γcosθ/ρgR
になる。水がガラス管を上昇する場合などはθはゼロとしてもよい。下降する場合も同様である。この式では、Rはhに比べ十分小さいとしている。この関係は、表面張力の値を測定するのに用いる。
[小野 周]
改訂新版 世界大百科事典 「毛管現象」の意味・わかりやすい解説
毛管現象 (もうかんげんしょう)
capillarity
capillary phenomenon
毛細管現象ともいう。液中に立てた細い管(毛細管)の中や,2枚の板の細隙の間の液体の高さと,外側の液体の高さとが食い違う現象。その原因は管の壁面を液体がぬらすかぬらさないかによって接触角が鋭角または鈍角になり,液面が上に凹あるいは凸になることにある。このとき表面張力によって管内の液中の圧力が外圧より小あるいは大となって,液体がそれに見合うだけ引き上げられる,あるいは引き下げられるのである。
いま図に示したように細管が半径aの円管で接触角がθであるとする。液面が曲率半径a/cosθの球面でほぼ近似できるとき,表面張力の大きさをγとすれば,圧力差は2γcosθ/aとなるから,液面の上昇hは,gを重力の加速度,ρを液体の密度とすると,ほぼ2γcosθ/ρ gaに等しい。これは,ほぼ2πaの長さの接触点に働く表面張力の上向きの成分2πaγcosθを,引き上げられた液柱に働く重力ρgh・πa2と等置して得られる結果にもなっている。接触角θが鈍角であればcosθは負となり,液面は下降(h<0)することになる。幅2aの細隙のときはh≒γcosθ/ρ gaとなる。また傾いた管では水平面から自由面までの高さがhとなる。aが小さい場合,例えば多孔質の物質中の孔,植物の師管(しかん)などでは,水のように壁をぬらす液体の浸透する距離は非常に大きくなる。
執筆者:橋本 英典
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「毛管現象」の意味・わかりやすい解説
毛管現象
もうかんげんしょう
capillarity; capillary phenomenon
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「毛管現象」の意味・わかりやすい解説
毛管現象【もうかんげんしょう】
→関連項目液体
出典 株式会社平凡社百科事典マイペディアについて 情報
化学辞典 第2版 「毛管現象」の解説
毛管現象
モウカンゲンショウ
capillarity, capillary phenomenon
液体中に細い管(毛管)を立てると,液が管の壁面をぬらす場合には外部液面より管の内部液面が高く上がり(毛管上昇),ぬらさない場合には管内液面が低くなる現象をいう.液面が管壁をよくぬらす場合(接触角 = 0°)には,毛管上昇の高さを測定して液の表面張力を求めることができる.[別用語参照]表面張力測定法
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
法則の辞典 「毛管現象」の解説
毛管現象【capillary phenomena】
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...