重相関係数（読み）ジュウソウカンケイスウ（英語表記）multiple correlation coefficient

デジタル大辞泉

じゅうそうかん‐けいすう〔ヂユウサウクワン‐〕【重相関係数】

重回帰式による予測値と実際に測定される値との相関関係の程度を示す数値。相関係数のうち、説明変数が2つ以上あるもの。－1から1までの値をとり、1に近いほど正の相関関係、－1に近いほど負の相関関係が強く、0に近いほど相関関係が弱い。2乗すると決定係数が得られる。

出典　小学館

日本大百科全書(ニッポニカ)

重相関係数
じゅうそうかんけいすう
multiple correlation coefficient

変数Yを他の変数（X₁、X₂、……、X_k）の上に線形回帰した場合、最小二乗法によって得られるYの（X₁、X₂、……、X_k）への回帰超平面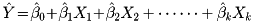

によって与えられるYと、観測値Yとの間の相関係数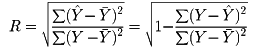

を、kが2以上の場合につき、Yと（X₁、X₂、……、X_k）との間の重相関係数という。

　たとえば、牛肉の需要量の動きYを、牛肉の価格X₁、豚肉の価格X₂、および人々の可処分所得X₃の三つの変数の動きとの関連で説明しようとするとき、最小二乗法の下では、線形関数として表される説明式Y＝β₀＋β₁X₁＋β₂X₂＋β₃X₃と実際のYの値との誤差の二乗和
　　Σ｛Y－(β₀＋β₁X₁＋β₂X₂＋β₃X₃)｝²
を最小にするように未知の係数β₀、……、β₃を求めることになる。変数Y、X₁、X₂、X₃についての観測データに基づいて求められたそれらの値をハット記号(^)つきのβ₀、……、β₃とすると、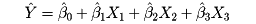

によって計算されるYなる値は、Yの変動のうち、変数X₁、X₂、X₃の変動によって説明される部分である。すなわち、変数Yの全変動中、どれほどの割合が他の3変数X₁、X₂、X₃の動きによって説明されているかは、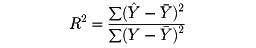

によって示されることになる。この値は、変数Yの他の変数（X₁、X₂、X₃）への回帰関係における決定係数とよばれ、それを平方で開き正の数として表されたRが相関係数である。そして、この例のように説明変数Xの数が複数個である多変数回帰によるものを、とくに重相関係数という。

［高島　忠］

[参照項目] | 回帰分析 | 最小二乗法

出典　小学館　日本大百科全書(ニッポニカ)

栄養・生化学辞典

重相関係数

　多変数に相関する量について，ある一つの変数と他の変数全部との間の相関係数．

出典　朝倉書店

世界大百科事典（旧版）内の重相関係数の言及

【回帰分析】より

…いいかえれば観測値と予測値ができるだけ近くなることが望ましい。そこで，観測値と予測値の相関係数を一般の重回帰分析にも通用するように重相関係数，その2乗を寄与率と呼んで，回帰式の観測値に対するあてはまりのよさを示す指標とする。回帰式としては，ŷ_i＝a＋blogx_iのようにx_iの簡単な変換式を用いたり，ŷ_i＝a＋bx_i＋cx_i²のように多項式を用いることもできる。…

※「重相関係数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」