デジタル大辞泉 「相関係数」の意味・読み・例文・類語
そうかん‐けいすう〔サウクワン‐〕【相関係数】
[補説]－1から1までの値をとり、1に近いほど正の相関関係、－1に近いほど負の相関関係が強く、0に近いほど相関関係が弱い。説明変数が1つの場合は単相関係数、2つ以上ある場合は重相関係数という。
Sponserd by 
[補説]－1から1までの値をとり、1に近いほど正の相関関係、－1に近いほど負の相関関係が強く、0に近いほど相関関係が弱い。説明変数が1つの場合は単相関係数、2つ以上ある場合は重相関係数という。
関連語
精選版 日本国語大辞典 「相関係数」の意味・読み・例文・類語
そうかん‐けいすうサウクヮン‥【相関係数】
- 〘 名詞 〙 相関関係の性質や程度を表わす数値。１とマイナス１との間にあり、正の相関関係があれば正、負の相関関係があれば負、その絶対値が相関関係の強さを表わす。〔日本の気象（1956）〕
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報 | 凡例
Sponserd by
最新 心理学事典 「相関係数」の解説
そうかんけいすう
相関係数
correlation coefficient
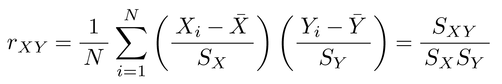
となる。ここでＮはデータ数，Ｘ̄，Ｙ̄およびＳX，ＳYはそれぞれ変量Ｘ，Ｙの平均，標準偏差，またＳXYは共分散を表わす。また，ｒXYの変域は－1≦ｒXY≦1となり，正の値をもつ場合には「変量ＸとＹとの間には正の相関がある」，その逆の場合は「負の相関がある」という。また絶対値が1に近いほど線形関係が強くなり，絶対値が1の場合はすべてのデータが直線上に並ぶ。逆に絶対値が0に近づくほど直線関係は見られなくなる。さらに，相関係数の絶対値は変量ＸとＹの線形変換に関して不変である。すなわちいずれの変量に定数を加算しても，あるいは定数倍してもその絶対値は変化しないという性質がある。
次に二つの変量がともに順序尺度である場合には，順位相関係数rank correlation coefficientが用いられる。これには，データから得られるすべての順序対の組み合わせ方によっていくつかの種類がある。そのうちスピアマンの順位相関係数は，積率相関係数の定義式を順位に置き換えて求められるもので，同順位がない場合には，
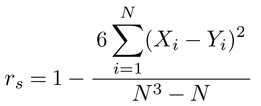
と表現される。またケンドールのτa（タウ エー）とよばれるものは，Ｎ（Ｎ－1）/2通りあるすべての順序対の組み合わせについて，変量Ｘにおける組み合わせ（Ｘj，Ｘk）とＹにおける組み合わせ（Ｙj，Ｙk）とにおいて，両者の大小関係が一致している対の数をＰ，また一致していない対の数をＱ，総数をＴ＝Ｐ＋Ｑとすると，同順位がない場合に，
τa＝
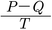
と定義されるものである。なお，Ｐ＋Ｑ＝Ｎ（Ｎ－1）/2である。同順位がある場合には，ケンドールのτb（タウ ビー）とよばれる係数が定義される。いずれの変域も積率相関と同じく，－1≦ｒs≦1および－1≦τa≦1となる。
さらに両方の変量とも名義尺度をなす場合，もしくは質的データが得られている場合には，分割表に整理してそこから変量間の関連性を見る。もし二つの変量とも二つの値しかとらない2値型変量であるならば，積率相関の定義式に2値データを代入して得られるφ（ファイ）係数phi-coefficient，または点相関係数point correlation coefficientともよばれる，
φ＝
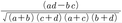
が用いられる。ここでａ，ｂ，ｃ，ｄは2変量の組み合わせがそれぞれ（1，1），（0，1），（1，0），（0，0）であったものの数である。またN＝a＋b＋c＋dである。ただし，φ係数に関してはその変域が－1≦φ≦1となるのが（ａ＋ｂ）/Ｎ＝（ａ＋ｃ）/Ｎ＝0.5の場合のみであることに注意が必要である。そのため2変量の後ろに2変量正規分布に従う潜在変数が仮定でき，観測変量としての2変量が2値型変量になっている場合には四分相関係数tetrachoric correlation coefficientを用いる方がよいとされる。2変量のうち二つの変量がそれぞれｋ，ｌ個の値を取る場合にはｋ×ｌ分割表についてクラメールの連関性係数measure of associationを求める。その定義式は，
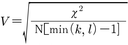
となる。ここでmin（ｋ，ｌ）はｋ，ｌの小さい方の数，χ2は分割表から求められたカイ2乗値，また変域は0≦Ｖ≦1である。
2変量のうちの一方が連続変量，もう一方が2値型変量である場合には，積率相関係数を整理して求められる点双列相関係数point biserial correlation coefficient，
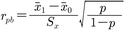
が利用できる。今変量ｘが連続変量，変量ｙが2値型変量とすると，ｘ̄1は変量ｙの値が1となる観測値のみについて求めた変量ｘの平均，ｘ̄0は変量ｙの値が0となる観測値のみについて求めた変量ｘの平均，ｐは変量ｙの平均である。もし2変量間に対して2変量正規分布が仮定できて，変量ｙのみが測定段階で2値型になったとすると，それらの間の相関係数のことを双列相関係数biserial correlation coefficientとよび，
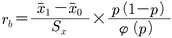
で定義される。ここでψ（ｐ）は，変量ｙの平均ｐに対応する正規分布の確率密度である。点双列相関係数ｒpbと双列相関係数ｒbとの間には，
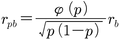
の関係があり，
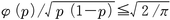であることが知られているから，つねに点双列相関係数の方が双列相関係数よりも低い値になることがわかる。実用的にはモデルとして2変量正規分布が無理なく仮定できるなら，双列相関係数を用いる方がよい。しかし，たとえば双生児研究において言語的能力の相関を求めるような場合，双生児の言語的能力のどちらを変量ｘ1あるいは変量ｘ2とするかは定かではない。このようなときは級内相関intra-class correlationが利用され，その定義式はｉ番目の双生児の組のデータ（ｘi1，ｘi2）の数をｎとして，
となる。ただし，
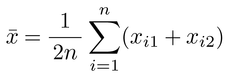
である。もしｉ番目のデータが（ｘi1，ｘi2，…，ｘij，…，ｘik）のようにｋ個の対からなる場合には，ｘ̄をすべてのデータの平均，
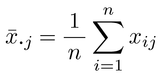
として，
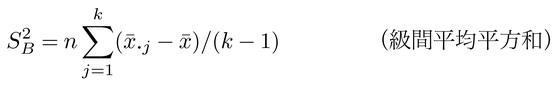
および
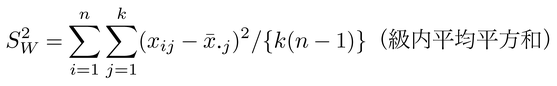
とすると，
で表現できる。さらに，たとえば無作為に選ばれたｋ人の評定者が無作為に選ばれたｎ個の小論文を評定するような場合には2要因の変量モデルを仮定し，あるいはそのどちらかを固定要因とする場合には混合モデル，さらには要因間に交互作用の有無を考える場合など，そのデータにふさわしい級内相関が存在する。また，級内相関はデータの等質性の指標ともみなせることから，パフォーマンス・アセスメントなどの評定結果の信頼性を求める際に，古典的テスト理論における信頼性係数に対応する係数として用いられることもある。
また，二つの変量に影響を及ぼす第3の変量ｚが存在する場合，二つの変量の両方からｚの影響を取り除いた後の相関を偏相関係数partial correlation coefficientといい，
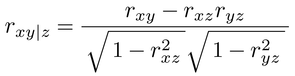
で定義される。それに対して，たとえば変量ｙからのみ変量ｚの影響を取り除いて変量ｘとの相関を求めたいときには部分相関係数semi-partial coefficient，part correlation coefficientとして，
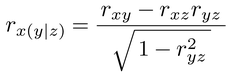
が用いられる。
さらに相関係数を利用する際の一般的な注意としては，⑴散布図上で2変量ともにその値が著しく大きなデータの組み合わせが両端に存在する場合には，相関係数の絶対値は大きくなりやすいこと，⑵たとえば年齢層ごとには相関が見られなくても，年齢をこみにすると年齢が第3の変数として機能して，いわゆる疑似相関が生じる可能性があること，⑶大学入試と入学後の相関のように，一方の変量のある値で分布が切断されると，切断されない場合に比べて相関の値が小さくなること，⑷相関があるからといって因果関係が存在するとはいえないこと，⑸相関が集団統計量であるにもかかわらず，相関の大きさをあたかも個人の特性であるかのように言明すること，⑹たとえば，二つの変量に関する複数の集団の平均から求めた相関は，同じ変数について個々のデータから求めた相関よりも大きな値を取るために解釈を間違う可能性があること（ロビンソンの生態学的誤謬とよばれる），⑺以上で述べた相関は，主として二つの変量の直線的な関係の強さを表現するのに適しているが，曲線的な関係をとらえるには不適切であること，その場合には相関比correlation ratioを使うべきことなどが指摘できる。ただし，相関比は，本来，一方の変量ｘが間隔尺度，他方の変量ｙがｋ個の値からなる順序尺度または名義尺度の場合に，変量ｙのｊ番目の値に属するｎj個のデータの変量ｘの平均をｘ̄・jとすると，
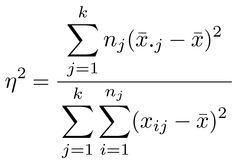
で定義されるものであるが，この場合はあたかも一方の変量を順序尺度か名義尺度であるかのようにみなして改めて離散変量に変換していることになる。
なお，相関係数の検定を行なう場合には，変量ｘとｙが2変量正規分布に従うと仮定して母相関係数ρに関する仮説を立てる。仮説の立て方には，⑴帰無仮説にρ＝0，対立仮説にρ≠0とする場合と，⑵帰無仮説にρ＝ρ0（≠0），対立仮説にρ≠ρ0とする場合がある。前者の場合は標本相関ｒを
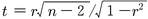と変換すれば，ｔが自由度ｎ－2のｔ分布に従うことを利用して検定を行なうことができる。それ以外は，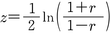
で表わされるフィッシャーのｚ変換Fisher's transformationを行ないｚの分布が平均（1/2）ln｛（1＋ρ）/（1－ρ）｝，分散1/（ｎ－3）の正規分布に近似される性質を利用して検定を行なう。その際も検定一般と同じくｎが大きい場合に帰無仮説が棄却されたからといって，ただちに相関が存在すると解釈してはならない。実質的に意味ある大きさなのかの吟味を必要とする。 →尺度
〔柴山 直〕
出典 最新 心理学事典最新 心理学事典について 情報
Sponserd by
日本大百科全書(ニッポニカ) 「相関係数」の意味・わかりやすい解説
相関係数
そうかんけいすう
correlation coefficient
ある観測対象集団について、個々の観測単位のもつある二つの属性に注目し、その値を観測したとき、両者の間に存在する直線的な関連の強弱を示す指標のこと。
いま、ある小学校の1年生の児童の集団を観測対象とし、その1人1人について身長と体重を測定することによって、両者の間の直線的な関連（一方の数値が変化すると他方の数値もある直線に沿う形で変化する関係）の強弱をみることとする。このとき、最初に測定した児童についての身長と体重の測定値の組を（X1,Y1）とし、以下同様にして、第i番目に測定した児童の測定値を（Xi,Yi）とする。そして、測定された児童の総数をnとすると、この1年生児童についての身長と体重との間の直線的な関連の強さの程度、すなわち相関係数Rは、次式によって計算される。
この式のなかで、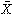
はX1、X2、……、Xn（身長の測定値）の平均値、
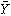はY1、Y2、……、Yn（体重の測定値）の平均値である。Rは、XとYの共分散をXおよびYのそれぞれの標準偏差の積で割ることによっても計算される。その値はかならずプラス1とマイナス1との範囲にあり、XとYの動きが完全に近い直線的関係になるほど絶対値は1に近い値となる。したがって、Rの値が逆に0に近くなるほどXとYとはその動きに関して無関係の状態に近づくことになり、Rが0ということは、完全な無相関を意味する。また、Rがプラスの値であれば、Xが増大するにつれてYも増大する関係にあること、Rがマイナスの値であれば、Xが増大するときYは逆に減少するという関係にあることを示す。
［高島 忠］
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by
ブリタニカ国際大百科事典 小項目事典 「相関係数」の意味・わかりやすい解説
相関係数
そうかんけいすう
correlation coefficient
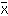，標準偏差をσx とし，Y についての測定値の平均値を ȳ，標準偏差をσy とすれば，相関係数 r は次式によって定義される。
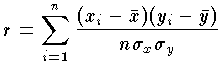r の値は －1≦r≦1 の範囲にあり，r＝0 を無相関という。これは，x の値によって y の値の変動への影響を表わす指標であって，r＞0 は x の傾向と y の傾向との一致の傾向，r＜0 は反対の傾向を意味する。これは，ベクトル空間の内積と同じ考えで，いわば2つのベクトル間の角の開き具合のようなものである。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by
百科事典マイペディア 「相関係数」の意味・わかりやすい解説
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by
ブランド用語集 「相関係数」の解説
相関係数
出典 (株)トライベック・ブランド戦略研究所ブランド用語集について 情報
Sponserd by
ASCII.jpデジタル用語辞典 「相関係数」の解説
相関係数
出典 ASCII.jpデジタル用語辞典ASCII.jpデジタル用語辞典について 情報
Sponserd by
栄養・生化学辞典 「相関係数」の解説
相関係数
Sponserd by
世界大百科事典（旧版）内の相関係数の言及
【数理統計学】より
…そのような考え方は母集団の概念を導入するうえで役だったのである。続いて，優生学の研究の創始者として知られるイギリスの科学者F.ゴールトンが現れ，人体測定研究所で調査した多数のデータを解説するために相関係数の概念を導入して統計学の新しい手法を開発した。これは回帰分析の方法に対して，先駆的な役割を果たすものとなった。…
【相関】より
…相関図でXの値が大きくなるとYの値が大きく(小さく)なる傾向があるとき，XとYは正(負)の相関にあるという。相関の強さを測る尺度として次の式で計算される相関係数が使われる。
ただし，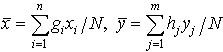
つねに－1≦r≦1である。…
【相関分析】より
…ある集団の特性が統計的変量としてとらえられるとき，例えば体重と身長の相関とか数学や英語のテスト結果の間の相関というように，相関係数を基本にして多数の変量間の相互依存性を分析する統計手法の総称。因子分析や正準相関分析を含む。…
※「相関係数」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponserd by