改訂新版 世界大百科事典 「最小二乗法」の意味・わかりやすい解説
最小二乗法 (さいしょうにじょうほう)
least square method
19世紀の初め,C.F.ガウスが天体の運動理論を展開するにあたって,多くの観測結果にもっともよく一致するよう軌道を決定するために開拓された方法で,応用範囲も広く,誤差論と一対をなしている。
ある未知量を測定するのに,十分注意を払っても偶発的な誤差を免れない。最小二乗法はこのような誤差を含む多くの測定値から真の値を有効に推定する統計的手法で,正規分布(ガウス分布)に基礎をおいている。ガウスの理論はこの分布の特徴づけから始まる。誤差を連続量とみて,その確率密度をφ(x)としよう。誤差がxとx+dx(dxは微小区間)との間にある確率はφ(x)dxで表される。未知量pを測定してMが得られたとすれば,誤差はM-pでその確率密度はφ(M-p)である。いまn個の同様な観測による測定値M1,M2,……,Mnが得られ,しかもすべての観測は独立な結果を生ずるものと仮定すれば,積φ(M1-p)φ(M2-p)……φ(Mn-p)=Ωは,すべてこれらの値が同時に得られる可能性,あるいは確率を表している。ここで関数φは対称(φ(-x)=φ(x))で滑らかとしておくのは自然で,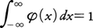 でなければならない。本質的な仮定として,観測値の算術平均,
でなければならない。本質的な仮定として,観測値の算術平均,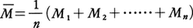 がpのもっともよい推定値を与えるものとしよう。すなわちp=のときΩが最大になると仮定する。特別な場合として,M2=M3=……=Mn=M1-nNなら=M1-(n-1)Nである。Ωはp=で極値をとるためlogφ(x)=ψ(x)とおくと,ψ′(M1-p)+ψ′(M2-p)+……+ψ′(Mn-p)はp=で0になることを用いてψ′((n-1)N)=-(n-1)ψ(-N)が出て,n,Nが任意でよいことから,
がpのもっともよい推定値を与えるものとしよう。すなわちp=のときΩが最大になると仮定する。特別な場合として,M2=M3=……=Mn=M1-nNなら=M1-(n-1)Nである。Ωはp=で極値をとるためlogφ(x)=ψ(x)とおくと,ψ′(M1-p)+ψ′(M2-p)+……+ψ′(Mn-p)はp=で0になることを用いてψ′((n-1)N)=-(n-1)ψ(-N)が出て,n,Nが任意でよいことから,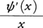 は定数となることが導かれる。すなわち
は定数となることが導かれる。すなわち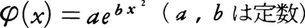 となる。全区間で積分して1となるため結局正規分布の密度関数,
となる。全区間で積分して1となるため結局正規分布の密度関数,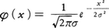 に到達する。観測の精密さは標準偏差の逆数h=σ⁻1,あるいはそれに比例する量で表される。
に到達する。観測の精密さは標準偏差の逆数h=σ⁻1,あるいはそれに比例する量で表される。
一般に未知量p1,p2,……,pνの関数V1,V2,……Vnがあって,それらの関数の観測値がそれぞれM1,M2,……,Mnであったとする。もし,これらの観測が同じ精密さで行われたと仮定すれば,上記のφと記号v1=M1-V1,v2=M2-V2,……,vn=Mn-Vnを用いて,未知量p1,p2,……,pνの最確値は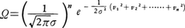 を最大にするもの,すなわちv12+v22+……+vn2を最小にするものとして定められる。もし各観測の精密さがh1,h2,……,hnで異なる場合には,h12v12+h22v22+……+hn2vn2を最小にするものを求めることになる。
を最大にするもの,すなわちv12+v22+……+vn2を最小にするものとして定められる。もし各観測の精密さがh1,h2,……,hnで異なる場合には,h12v12+h22v22+……+hn2vn2を最小にするものを求めることになる。
例えば未知量がただ一つのpで,関数a1p+b1,a2p+b2,……,anp+bnの値M1,M2,……,Mnが同じ精密さで観測されたとすれば,pの最確値はMiの補正値mi=Mi-biを用い,(m1-a1p)2+(m2-a2p)2+……+(mn-anp)2を最小にするpの値,すなわち, で与えられる。
で与えられる。
次の例は未知量は複数個,例えばp1,p2,p3,p4と4個あるが,関数V1,V2,……はやはりそれら未知量の一次関数の場合である。vi=Mi-Vi=-mi+aip1+bip2+cip3+dip4(i=1,2,……)としよう。W=v12+v22+……とおき,これを最小にすることを考える。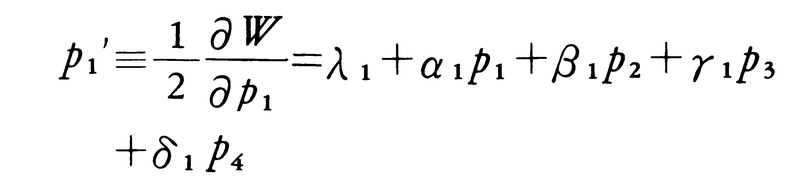
および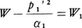 とおく。このときα1>0であることに注意する。またW1はp1を含まないことは
とおく。このときα1>0であることに注意する。またW1はp1を含まないことは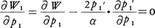 からわかる。次に,
からわかる。次に,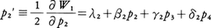 および
および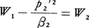 とおく。W2はp1もp2も含まない。またβ2>0である。同様に,
とおく。W2はp1もp2も含まない。またβ2>0である。同様に,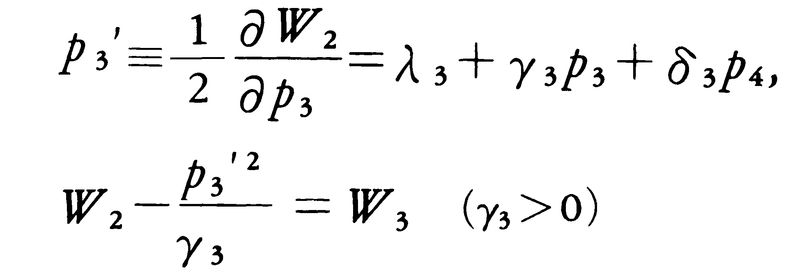
そして最後に,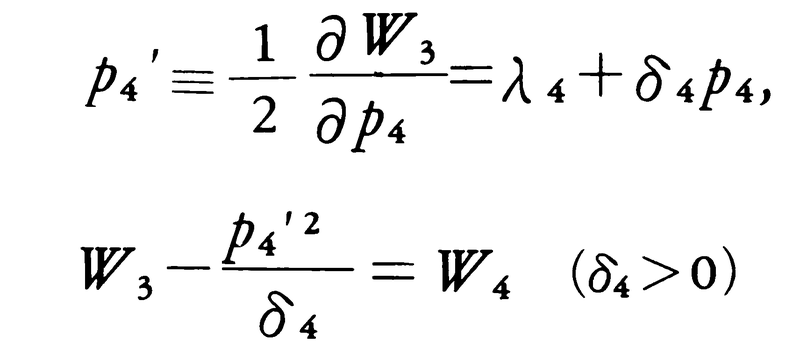
に至る。このW4は定数cでなければならない。したがって,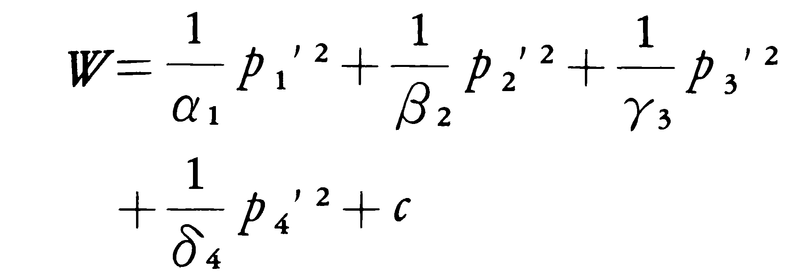
である。ところで(p1,p2,p3,p4)に対する確率密度は,
exp(-W/2σ2)に比例している。p1が不確定のままなら残りの量の確率密度は,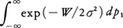 すなわち
すなわち
exp(-W1/2σ2)に比例する。p2も変量として扱えば(p3,p4)に対しては
exp(-W2/2σ2)
を考え,最後にp3も変量としてp4に対する確率密度は
exp(-W3/2σ2)に比例するとしてよい。よって未知量が一つの場合に帰着され,p4の最確値,
-\(\frac{λ4}{δ4}\)
が得られる。あとは逐次p3,p2,そしてp1の最確値を決めていくことになる。Viが一次関数と限らない一般の場合にも同様な手法が考えられている。
→誤差
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「最小二乗法」の意味・わかりやすい解説
最小二乗法
さいしょうじじょうほう
二乗和を最小にする方法。もっとも簡単な例は、x1, x2,……, xnが与えられたとき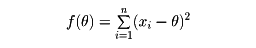
を最小にするようにθを定める問題で、この場合には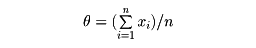
のときf(θ)が最小になる。
次の例は回帰直線である。二つの変量X、Yについての測定結果を
(x1, y2), (x1, y2),……, (xn, yn)
とするとき、xy平面上の直線y=mx+bに含まれる定数m、bを、二乗和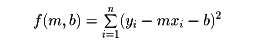
が最小になるように定めると、YのXに関する回帰直線が得られる。これも二乗和を最小にする方法である。
次に連立一次方程式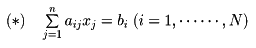
を考えよう。方程式の数Nが未知数の数nより大きいとき、一般にはこの連立一次方程式は解をもたない。このような場合も含めて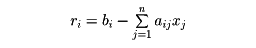
と置いて、二乗和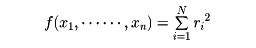
を最小にするようにx1, x2,……, xnを定める方法が最小二乗法である。連立一次方程式(*)が解をもつこととfの最小値が0であることとは同等である。f(x1,……, xn)を最小にするx1, x2,……, xnは、次の連立一次方程式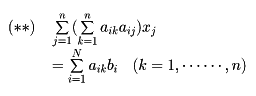
を解いて求められる。この方程式(**)を正規方程式という。
最小二乗法は統計学において母数を推定する場合にも用いられる。X1, X2,……, Xnは独立な確率変数で、各Xiの平均値が未知の母数θ1,θ2,……,θkを含むものとする。
E(Xi)= i(θ1,θ2,……,θk) i=1,……, n(X1, X2,……, Xn)の実現値(x1, x2,……, xn)が与えられたとき、二乗和
i(θ1,θ2,……,θk) i=1,……, n(X1, X2,……, Xn)の実現値(x1, x2,……, xn)が与えられたとき、二乗和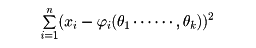
を最小にするようなθ1,θ2,……,θkの値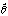 1,
1,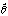 2,……,
2,……,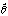 kをθ1,θ2,……,θkの推定値とするのである。
kをθ1,θ2,……,θkの推定値とするのである。
[古屋 茂]
最新 地学事典 「最小二乗法」の解説
さいしょうにじょうほう
最小二乗法
method of least squares
観測値のデータ処理の一方法。観測値とパラメーターの間にある関数関係を利用してパラメーターを求めようとする際,観測値に誤差があるため精密な値が決定できない。さらに通常は誤差を考慮して未知のパラメーターの数以上に観測を繰り返すので,この点からも一義的には決定できない。そこで観測値にある補正を加えた値が正しい値になると考え観測方程式(observation equation)を立て,この補正の二乗和が最小となるという条件のもとに正規方程式(normal equation)を導きパラメーターの値を推定する。通常は,観測の誤差は正規分布するとして観測の重みも考えて処理する。この場合の誤差処理の数学モデルをガウス-マルコフ・モデル(Gauss-Markov model)という。誤差の分布法則が近似的にしかわからないときのパラメーター推定をベイジャン推定(Baysian estimation)という。 y=f(x1, x2,……,xn)のように関数関係が少なくとも近似的にわかっているときi(>n)個の測定を行ってyの実測値を得たときには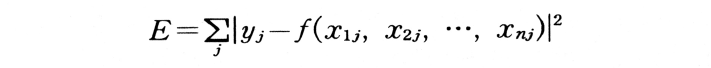
なる二乗誤差Eを最小にする条件(式fの係数など)を求める。結晶構造精密化においては,構造因子の観測値および計算値をFoおよびFc,スケール因子をk, i番目のパラメーターをpi, 荷重をwhとすると,R≡Σhwh(|Fo|h-k|Fc|h)2を最小にする値を通常求める。正規方程式をM・X=Δとし,パラメーターの数をnとするとMはn×nのマトリックスで,そのij成分は Mij=Σh{wh・∂(kFc)/∂Pi・∂(kFc)/∂Pj}となり,XはΔPiを成分とするベクトル,ΔはΣh{wh(Fo-kFc)・∂(kFc)/∂Pi}を成分とするベクトルである。
執筆者:丸茂 文幸・藤井 陽一郎
出典 平凡社「最新 地学事典」最新 地学事典について 情報
ブリタニカ国際大百科事典 小項目事典 「最小二乗法」の意味・わかりやすい解説
最小二乗法
さいしょうじじょうほう
method of least squares
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「最小二乗法」の意味・わかりやすい解説
最小二乗法【さいしょうにじょうほう】
→関連項目ルジャンドル
出典 株式会社平凡社百科事典マイペディアについて 情報
栄養・生化学辞典 「最小二乗法」の解説
最小二乗法
世界大百科事典(旧版)内の最小二乗法の言及
【統計的推定】より
… ![]() は,各xiと期待値μの偏差平方和, s=(x1-μ)2+……+(xn-μ)2を最小にするμの値に等しい。これはもっと複雑な問題で,xiの期待値が未知パラメーターμ1,……,μpの線形結合li1μ1+……+lipμpで表されているときに偏差平方和,
は,各xiと期待値μの偏差平方和, s=(x1-μ)2+……+(xn-μ)2を最小にするμの値に等しい。これはもっと複雑な問題で,xiの期待値が未知パラメーターμ1,……,μpの線形結合li1μ1+……+lipμpで表されているときに偏差平方和,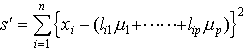 を最小にするような推定方式(最小二乗法)の特別な場合に当たる。最小二乗法による推定量は一般にxiが等分散,無相関のとき線形最良推定量であることが示される。…
を最小にするような推定方式(最小二乗法)の特別な場合に当たる。最小二乗法による推定量は一般にxiが等分散,無相関のとき線形最良推定量であることが示される。…
※「最小二乗法」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

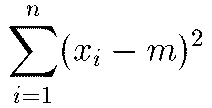 を
を