回帰分析（読み）カイキブンセキ（その他表記）regression analysis

デジタル大辞泉

かいき‐ぶんせき〔クワイキ‐〕【回帰分析】

ある変数が他の変数とどのような相関関係にあるのかを推定する統計学的手法の一。原因となる変数x（説明変数）と、結果となる変数y（目的変数または被説明変数）の間に、回帰式y＝ax＋bと表される関係があるとすると、x、yの観測値から最小二乗法を用いてa、bが求められる。この回帰式をもとに将来予測や要因分析を行う。

出典　小学館

最新 心理学事典

かいきぶんせき
回帰分析
regression analysis

回帰分析とは，関心の対象となっている変数群を，説明や予測をするための説明変数explanatory variable（予測変数，独立変数などともよばれる）と，その基準となる従属変数dependent variable（基準変数などともよばれる）に分け，両者の間に統計モデルを設定し，その間の関係を推論する手法である。その統計モデルは，線形回帰モデルと非線形回帰モデルに大別される。

【線形回帰モデルlinear regression model】　線形回帰モデルとは，従属変数ｙを，ｐ個の説明変数ｘ¹，…，ｘ^pによって予測・説明するために，回帰係数regression coefficient b^j（ｊ＝1，…，ｐ）を乗じた説明変数の和に切片ｃを加えた予測式



を考え，これと従属変数との誤差e＝y－y＾の大きさを最小にするｂ¹，…，ｂ^p，ｃを求める統計解析法を指す。

【単回帰分析と重回帰分析】　ｐ＝1つまりｙ＾＝bx＋cと表わせる分析とｐ≧2の分析を区別したいときは，前者を単回帰分析simple regression analysis，後者を重回帰分析multiple regression analysisとよぶ。個体を表わす添え字ｉ（＝1，…，ｎ）を各変数につけると，予測式は



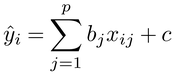
と表わせ，これを，従属変数を予測式と誤差の和とする式ｙⁱ＝ｙ＾ⁱ＋ｅⁱの右辺に代入した



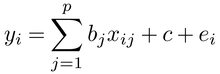
が回帰分析のモデル（回帰モデル）となる。

【切片と係数の最小2乗解】　誤差の2乗和



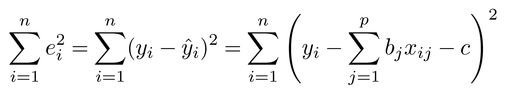
を最小にするｂ¹，…，ｂ^p，ｃが最小2乗解となる。従属変数・説明変数の平均を



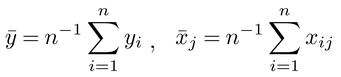
と表わすと，切片ｃの解は



と表わせ，これを回帰モデルのｃに代入すると



となり，平均偏差得点ｙ̃ⁱ＝ｙⁱ－ｙ̄，ｘ̃^ij＝ｘ^ij－ｘ̄^jを用いてモデルを整理すると，



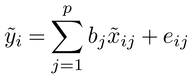
が得られる。この式から，平均偏差得点の回帰分析は，切片ｃが0になって消える以外は，素データの分析と同等であることがわかる。

　ｎ個体すべての平均偏差得点，係数，誤差を



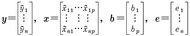
のようにベクトルと行列で表わせば，回帰モデルはy＝Xb＋eと書け，係数ベクトルｂの解は



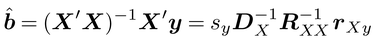
で与えられる。ここで，Ｒ^XXは説明変数同士の相関係数からなるp×pの行列，ｒ^Xyはｐ個の説明変数と従属変数の相関係数からなるｐ×1のベクトル，Ｄ^Xは各説明変数の標準偏差を対角に配する対角行列，ｓ^yは従属変数の標準偏差である。全変数を平均0，分散1，つまりｓ^y＝1かつＤ^Xが単位行列となる標準得点に変換したデータに回帰分析を適用すると，前段のｂ＾からｓ^yＤ^-1Xが消えたＲ^-1XXｒ^Xyがｂの解となって，切片が0となる以外は，素データを分析した場合と同じ結果が得られる。この解をとくに標準解standardized solutionとよぶ。単回帰分析の回帰係数の標準解は，従属変数と説明変数の相関係数に一致する。

【分散説明率と重相関係数】　解ｂ＾＝［ｂ＾¹，…，ｂ＾^p］′，ｃ＾と説明変数の値を予測式に代入して得られる予測値



従属変数ｙⁱ，および残差ｅ＾ⁱ＝ｙⁱ－ｙ＾ⁱは，次の性質をもつ。⑴残差ｅ＾ⁱの平均ｅ̄は0となり，平方和



に基づく残差分散ｓ^2eを，総体的な残差の大きさとみなせる。⑵予測値ｙ＾ⁱの平均は，従属変数の平均ｙ̄に等しい。⑶ｙⁱとｙ＾ⁱの共分散ｓ^yŷは，ｙ＾ⁱの分散ｓ^2ŷに等しい。⑷従属変数の平方和は，



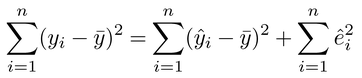
のように分割され，これを平方和の分割decomposition of sum of squaresとよぶ。

　この分割より従属変数ｙⁱの分散ｓ^2yについて，



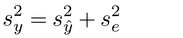
が導かれ，この両辺をｓ^2yで割ると



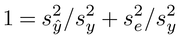
が得られ，従属変数の分散に対する予測値の分散の比率



が，0以上1以下の値を取って，残差の小ささを表わすことがわかる。この比率ｓ^2ŷ/ｓ^2yは，決定係数coefficient of determinationまたは分散説明率proportion of variance accounted forとよばれ，従属変数の分散のうち，ｐ個の説明変数の分散によって説明される成分の割合と解される。さらに，前段⑶の性質ｓ^2ŷ＝ｓ^yŷを分散説明率ｓ^2ŷ/ｓ^2yに代入すると



となり，予測値と従属変数の相関係数ｒ^yŷ＝ｓ^yŷ/ｓ^yｓ^ŷの2乗が分散説明率に等しいことがわかる。ｐ≧2のときのｒ^yŷは，説明変数と従属変数の重相関係数multiple correlation coefficientとよばれ，複数変数と一つの変数との相関の指標となる。正規分布を仮定する場合，「母集団では分散説明率と重相関係数は0である」という仮説を，分散分析によって検定できる。

【偏回帰係数partial regression coefficient】　ｐ≧2のときに説明変数ｘ^jにかかる回帰係数ｂ^jを，とくに偏回帰係数とよぶ。これによって，ｘ^j以外の説明変数の影響を除いたｘ^jの効果を把握できるのが，重回帰分析の利点である。たとえば，商品の質ｘ¹だけから商品の売上ｙを予測する単回帰分析では，「質ｘ¹が高いと値段ｘ²も高いので，売上ｙは下がるため，質ｘ¹にかかる係数が負になる」というように，分析に投入されない変数ｘ²の効果が結果に混入する。これに対し，商品の質ｘ¹と値段ｘ²の両者から売上ｙを予測する重回帰分析では，値段ｘ²の影響を除いたときに質ｘ¹が売上ｙへ及ぼす効果を，偏回帰係数ｂ¹によって把握できる。仮説「偏回帰係数＝0」の検定と係数の区間推定には，ｔ分布が用いられる。分散の異なる説明変数の間で従属変数への効果の大小を比較するときは，標準解の偏回帰係数である標準偏回帰係数standardized partial regression coefficientを参照しなければならない。

【変数選択variable selection】　説明変数ｘ¹，…，ｘ^pすべてを分析に投入するのではなく，回帰モデルの適合度が高い説明変数の部分集合を求めることを変数選択とよぶ。たとえば，ｐ＝3であれば，計7通りの部分集合｛ｘ¹｝，｛ｘ²｝，｛ｘ³｝，｛ｘ¹，ｘ²｝，｛ｘ¹，ｘ³｝，｛ｘ²，ｘ³｝，｛ｘ¹，ｘ²，ｘ³｝のそれぞれからｙを予測する回帰分析を行ない，適合度が最大となる集合による分析結果を採択すればよい。適合度指標の一つに自由度調整済み重相関係数multiple correlation coefficient adjusted for the degrees of freedomがあり，これは説明変数が多いほど値が高くなる重相関係数の短所を補正した統計量である。説明変数が多いときは変数集合を網羅的に考慮できないので，適当な初期変数集合から始めて，適合度を高める説明変数の投入，あるいは適合度を下げる変数の除去，あるいは変数の取捨選択を繰り返して，望ましい変数集合にたどり着く方法が使われ，取捨選択を繰り返す方法はステップワイズ法stepwise methodとよばれる。

【多重共線性multicollinearity】　ｂ＾＝ｓ^yＤ^-1XＲ^-1XXｒ^Xyのように偏回帰係数の解は相関行列Ｒ^XXの逆行列の関数であるため，説明変数同士の相関が非常に高い場合に，たとえば偏回帰係数の信頼区間が負から正にわたるなど，解が不安定になる現象を多重共線性とよぶ。各説明変数が多重共線性の原因になっているか否かを診断するために，その変数と他のｐ－1個の説明変数の重相関係数を利用できる。

【他の回帰分析】　従属変数が複数（ｑ個）であり，それぞれの平均偏差得点と偏回帰係数を行列



にまとめ，Ｅを誤差行列とすれば，モデルがY＝XB＋Eと表わせる分析を多変量回帰分析multivariate regression analysisという。ただし，Ｂの解は（Ｘ′Ｘ）^-1Ｘ′Ｙで与えられ，その第ｊ列は，Ｙの第ｊ列を従属変数とした重回帰分析の解と同じになる。列数がｐとｑより少ない行列Ｗを用いて，p×qのＢが行列の積WVに等しいと制約した多変量回帰分析は縮小ランク回帰reduced rank regressionとよばれる。

【非線形回帰モデルnon-linear regression model】　非線形回帰モデルは，従属変数を説明変数の線形式に限らず，一般的な関数によって説明するものである。たとえば，従属変数ｙⁱが正答⑴と誤答（0）のように2値，説明変数ｘ^ijは連続変数のときに，その確率



を予測式とする分析をロジスティック回帰分析logistic regression analysisとよぶ。なお，非線形回帰モデルにおいて，従属変数の分布の系統的成分が，未知パラメータの線形式で表現されるとき，一般化線形モデルgeneralized linear modelとよばれる。　→因果分析　→構造方程式モデル　→相関係数　→多変量解析
〔足立 浩平〕

出典　最新 心理学事典

日本大百科全書(ニッポニカ)

回帰分析
かいきぶんせき
regression analysis

ある変数の動きが、他のどのような変数を原因としておこされるものであるか、その影響力はどれほどのものであるか、その変動全体のどれほどの部分がそれらの他の変数によって説明されるのかなどの問題を、統計的手法を用いて数量的に解析すること。

［高島　忠］

線型回帰モデル

いま、ある変数Yがk個の他の変数X₁、X₂、……、X_kの影響を受けて変動すると考えられるとき、その関係は、a₀、a₁、a₂、……、a_kを定数として
　　Y＝a₀＋a₁X₁＋a₂X₂＋……＋a_kX_k＋V
と表される。ここで、Vはこの関係式に採用されたk個の変数以外の要因からくるYへの影響を集約して表現する変数であって、その値は、なんらかの確率的な法則に従って発生するものと考えられる。X₁、X₂、……、X_kは説明変数、Yは被説明変数、そしてVは確率攪乱(かくらん)項とそれぞれよばれる。

　以下、取扱いを簡単にするために、説明変数が1個である場合について述べよう。Xがx₁の値のときYはy₁であり、x₂のときy₂であるというように、XとYに関して対応するデータをn組とする（観測する）。そして、それぞれの場合におけるX以外の要因の効果を表すもの、つまり、確率攪乱項をv₁、v₂、……、v_nとすると、
y_i＝a＋bx_i＋v_i (i＝1，2，……，n)
となる。これは、もっとも簡単な線型回帰モデルである。

［高島　忠］

パラメータ（係数）の推定

n組のデータ（x₁,y₁）,（x₂,y₂）,……,（x_n,y_n）から未知の係数a、bを求めるには、最小二乗法が用いられる。それは、この方法によって得られるa、bの推定量â、が、確率攪乱項v_iに関するある仮定の下で、推定式として統計的に望ましい性質を備えているからである。

　推定量â、を用いて計算されるy_iの値と実際の観測値y_iとの誤差をe_iとすると、â、は、その誤差の2乗和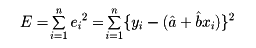

が最小になるように求められる。すなわち、Eが極値をとる条件として、âおよびでそれぞれ偏微分したものを0とおいて、

という連立方程式が得られる。これは、線型回帰モデルの未知のパラメータa、bの値を推定するための正規方程式とよばれる。これを解くことによって、âとは次のように得られる。

ここで、Σはすべてiについての1からnまでの和を表す。

［高島　忠］

回帰直線の性質

このようにして求められる回帰係数については、正規方程式の第1式から、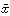、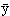をそれぞれx_iおよびy_iについての平均値として
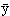　　＝â＋
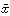
の関係のあることがわかるので、回帰直線は、XおよびYの観測値の各平均値を座標とする点(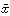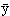，)を通る。また、誤差e_iの総和は0となるので、観測値を描いたグラフ上で、回帰直線より上方にある観測点から回帰直線までの距離の総和は、下方にある観測点から回帰直線までの距離の総和にかならず等しい。

［高島　忠］

決定係数

変数yに対する変数xの影響力（説明力）の強さは、回帰直線に対する変数y_iのばらつきの大きさによって測られる。

　それは、_iを回帰係数を用いたy_iの計算値とするとき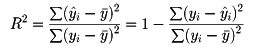

として表され、決定係数とよばれる。

［高島　忠］

『森田優三著『新統計概論』（1974・日本評論社）』▽『J・ジョンストン著、竹内啓他訳『計量経済学の方法』（1975・東洋経済新報社）』

[参照項目] | 回帰係数 | 計量経済学 | 最小二乗法

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

回帰分析 (かいきぶんせき)
regression analysis

なんらかの操作や活動の結果を予測したり，その結果の変動を制御したりするための手法で，統計的多変量解析の一つ。操作や活動のデータとそれに対応する結果のデータの組を多数集め，予測の対象とする量（目的変数もしくは従属変数と呼ぶ）の変動を，操作や活動のデータのうちその変動を説明する要因と考えられるデータ（説明変数もしくは独立変数と呼ぶ）によって予測するために，両者の関係を求めることをいう。製鉄所の炉の制御や化学工場での操業条件の決定のための工程解析をはじめ，経済データの分析や予測，心理学や医学など，多くの分野でもっともよく使われる統計的手法である。

　身長の高い父親からは身長の高い息子が生まれる傾向（相関関係）がある。x軸に父親の身長，y軸に息子の身長をとり，多くの家族のデータを散布図に表現し，x軸を小区間に分割し，各区間に含まれるyの値を平均し，それらの点をむすぶとほぼ直線になる。ここで，身長の高い父親から生まれた息子の平均身長は父ほど高くなく，身長の低い父親から生まれた息子の平均身長は父ほど低くないという関係がある。F.ゴールトンは1889年この関係を発見し退行と名づけ，直線を退行直線もしくは回帰直線と名づけた。これが回帰という名称の起源である。その後他分野にも適用され，説明変数と目的変数の関係が曲線の場合や一つの目的変数に対応する説明変数が多数ある場合にも回帰分析が行えるようになった。

　説明変数が一つのとき単回帰または直線回帰分析，二つ以上のとき重回帰分析ということがある。単回帰分析では，目的変数の第i番目の値をŷ_i，対応する説明変数の値をx_iとすると，直線ŷ_i＝a＋bx_iを回帰式と呼び，定数項aと偏回帰係数といわれるこう配bをいわゆる最小二乗法で推定する。すなわち，観測値y_iと予測値といわれる回帰式上の値y_iとの差r_i＝y_i－ŷ_iを残差といい，その残差の2乗の和（残差平方和）を最小にするaとbを求める。いいかえれば観測値と予測値ができるだけ近くなることが望ましい。そこで，観測値と予測値の相関係数を一般の重回帰分析にも通用するように重相関係数，その2乗を寄与率と呼んで，回帰式の観測値に対するあてはまりのよさを示す指標とする。回帰式としては，ŷ_i＝a＋b logx_iのようにx_iの簡単な変換式を用いたり，ŷ_i＝a＋bx_i＋cx_i²のように多項式を用いることもできる。重回帰分析では，説明変数をx，z，……などと書いて，回帰式をŷ_i＝a＋bx_i＋cz_i……などとする。回帰分析では多数の変数が説明変数の候補と考えられるが，実用上は数個（3～7個，たかだか10個程度）の説明変数を選んであてはまりのよい回帰式がほしい。データの個数としては説明変数の数の10倍ぐらいはあってほしい。

　回帰分析を行うときのデータは，よく管理された実験で得られるデータとは限らず，日常の活動の中で記録されたものであることが普通である。そこで，回帰分析を行う人も，その結果を利用する人も，まず，データの質を検討し，あてはめられた回帰式の妥当性を検証することが必要である（そうすることを回帰診断ということもある）。データの質としては，外れ値の有無と共線性を検討する。大部分のデータの変動の範囲に比べて孤立して飛び離れた位置にあるデータを外れ値といい，それは各変数の分布や散布図を見るほかに残差の分布を調べることによって検出される。すべての外れ値が誤ったデータというわけではないが，外れ値の原因を調べたり，その外れ値を除外して回帰式を求めた場合の変化をみることによって価値ある情報が得られることが多い。実際に操業中の工程で観測されたデータはよい製品を作るために管理された状態での値であるから，実験なら説明変数の値を自由に変えられても，実際には説明変数の間に高い相関をもつことが多い。説明変数間に高い相関があることを一般に共線性があるという。そのようなとき推定した回帰式の係数は信頼度の低いものとなり，回帰係数の符号も予想とは逆になることがある。多くの説明変数があるとき，説明変数を増せば寄与率は高くなるが，その回帰式を用いて予測してもかえって誤差は大きくなり，制御に利用しても不安定となる。そこで，いろいろな観点から回帰式の妥当性を比較する基準をつくって適当な説明を選択して回帰式を求める手法が開発されている。それらは変数選択法あるいはモデル選択法と呼ばれ，コンピューターのソフトウェアとしても整備されてきている。最後に得られた回帰式をはじめとする知見は，新たなデータを観測してそのデータを十分に説明するかどうかによって検証することが望ましい。
→相関分析
執筆者：吉沢 正

出典　株式会社平凡社「改訂新版　世界大百科事典」

人材マネジメント用語集

回帰分析

・回帰分析 regression analysis
・説明変数と目的変数の関係を回帰式で表し、目的変数が説明変数によってどの程度
説明できるかを定量的に分析することである。
・回帰式は、y=ax+b(x:説明変数、y:目的変数)で表される。
・目的変数とは予測や要因分析を行う変数のことで、説明変数とは目的変数に影響を
与えると考えられる変数のことである。
・回帰式を求めるのに変数a、切片bを推定する。推定には最小二乗法を用いる。最小
二乗法は、観察された各点(x,y)と回帰線上の各点(x,yi)との残差dの平方和が最小
となる直線を求める方法である。
・回帰分析は、予測・要因分析等に用いられる。例えば、過去の生産量と製造費用の
データから回帰式を求め、将来の生産量に対する製造費用の予測に活用される。この
場合、生産量(x)に対する製造費用(y)の過去のデータから回帰式を推定する。生産
量(x)1単位当りの製造費用(y)がどれ程増加するかを示す傾きaは変動費、切片bは
固定費となる。将来の生産量(x1)を回帰式に代入すると将来の製造費用(y1)が導
かれる。
・予測をする際には、回帰式の精度の良さの尺度となる決定係数(0〜1の値)が1に
近い(当てはまりが良い)のが望ましい。
・また回帰分析は、因果関係が想像される2つの変数の関係を調べるのに用いられる
が、回帰式は、ある変数が増加(減少)すれば、もう一方の変数が増加(減少)する
という関係性を示しているだけで、変数間に因果関係が本当に存在するかは注意して
判断しなければならない。

出典　(株)アクティブアンドカンパニー

ブリタニカ国際大百科事典 小項目事典

回帰分析
かいきぶんせき
regression analysis

2つの変数 x と y の間に，y＝a＋bx ( a ，b は定数パラメータ) のような線形関係の数式モデルを仮定して，x と y についてのいくつかの観測あるいは測定データから，最小二乗法により未知パラメータ a ，b を推定する方法。 y を目的変数，x を説明変数という。理学，工学で実験式を求める場合や，経済学で経済 (予測) モデルをつくるのに，広く用いられる。説明変数が2つ以上あるときは，重回帰分析と呼ばれる。

出典　ブリタニカ国際大百科事典 小項目事典

ブランド用語集

回帰分析

回帰分析とは独立変数と従属変数の間の関係を推定するための統計的手法のことをいう。独立変数が1つなら単回帰分析、独立変数が2以上なら重回帰分析という。一次式を用いた線形回帰モデルが用いられることが多いが、それ以外の式を用いた非線形回帰モデルもある。

出典　(株)トライベック・ブランド戦略研究所

栄養・生化学辞典

回帰分析

　二つもしくはそれ以上の因子の間の関連性を回帰線などを用いて分析する操作．

出典　朝倉書店

世界大百科事典（旧版）内の回帰分析の言及

【季節変動】より

…一つは経済データを作成する政府系機関等がよく用いるもので，考える変数の原系列を適当な長さの移動平均で割って季節指数を求め，さらにこれを年間平均が100になるように調整したうえで，原系列に適用することによって季節変動を除去した系列が求められる。これに対して，回帰分析を用いる方法も存在する。考えている変数の中･長期的な変動を説明する変数とともに，季節ダミーを回帰式の右辺に導入し，季節変動の部分を後者によってとらえようとするものである。…

※「回帰分析」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」