電磁ポテンシャル（読み）でんじポテンシャル（英語表記）electromagnetic potential

改訂新版　世界大百科事典

電磁ポテンシャル (でんじポテンシャル)
electromagnetic potential

電場をE，電束密度をD，磁場をH，磁束密度をB，電荷密度をρ，電流密度をiとして，rotE＝－\(\frac{∂B}{∂t}\)，rotH＝\(\frac{∂D}{∂t}\)＋i，divD＝ρ，divB＝0で表されるマクスウェルの方程式を解いてEやBの各成分をきめることは，六元連立微分方程式を解くことであり，任意の電流・電荷分布についてこれを行うことはほとんど不可能である。しかしEやBの各成分はまったく独立というわけでなく，上記のマクスウェルの方程式自身によって束縛されている。例えばBの各成分はdivB＝0を満たさなければならない。そこでBの各成分を一つのベクトルAを用いて，

　B＝rotA　……（1）　

の演算から誘導することにしておけば，divB＝0は自動的に満足される。同じようにEの各成分はAのほかに，もう一つスカラー関数φを用い，

　E＝－gradφ－\(\frac{∂A}{∂t}\)　……（2）　

から導くことにしておけば，（1）とあわせてrotE＝－\(\frac{∂B}{∂t}\)の式は自動的に満足される。φとAを用いて残る二つの方程式を書き直すと，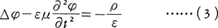

および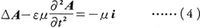

のようにまったく同形の非斉次波動方程式が得られる（εは誘電率，μは透磁率）。ただし，φやAのもつ不定性を利用して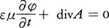，という条件を付加してある。つまりマクスウェルの方程式は事実上一つの2階微分方程式に帰着されたことになる。φおよびAをそれぞれスカラーポテンシャル，ベクトルポテンシャルといい，この両者をあわせて電磁ポテンシャルという。この非斉次ポテンシャル方程式は一般的に解けて，座標r，時刻tでのポテンシャルの値は，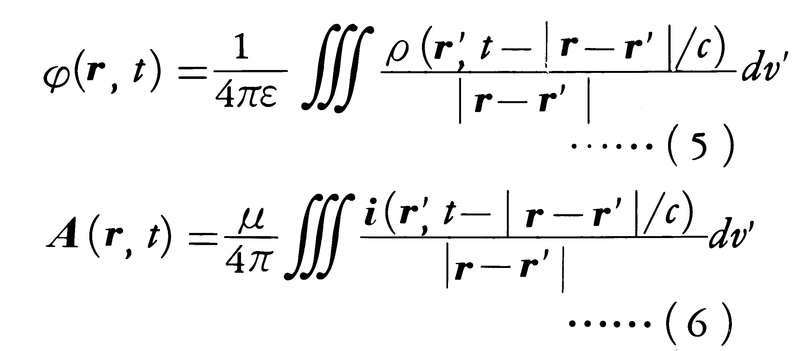

で表されるように，r′にある電荷または電流の，時刻t－｜r－r′｜/cの値の影響を重ねあわせたものとして求められる。ここでcは真空中の光速度である。この時刻のずれは，電磁的影響が光速で，r′からrにまで伝わる時間を表している。（5）（6）を遅延ポテンシャルという。電場や磁場は（1）（2）に従ってポテンシャルに微分演算を施すだけで求められる。

　電磁ポテンシャルは，このように電場や磁場を導くのに便利なものであるが，それらは単に数学的方便にすぎないものであろうか。ポテンシャル自身が物理的意味をもつと考える立場があり，Aは0でないが，B（＝rotA）は0であるような場を通ってきた荷電粒子の位相にずれが生ずることが指摘されている。例えば電子の干渉のようすが，このようなAの存在によって影響を受けるならば，Aの実在としての意味が証せられることになる。これについていくつかの実験がなされてきたが，まだ決着がついたという段階ではない。ところでこの場合も観測にかかる量，例えば二つの行路を通ることにより，電子の状態関数に生ずる位相の差はゲージのとり方により変わることはない。
→マクスウェルの方程式
執筆者：清水 忠雄

出典　株式会社平凡社「改訂新版　世界大百科事典」