マクスウェルの方程式（読み）マクスウェルノホウテイシキ（英語表記）Maxwell's equations

デジタル大辞泉

マクスウェル‐の‐ほうていしき〔‐ハウテイシキ〕【マクスウェルの方程式】

電磁場の時間的・空間的変化を記述する基本的な方程式。ファラデーの電磁誘導の法則を表す式、電流の磁気作用についてのアンペールの法則を一般化して表す式、電場および磁場についてのガウスの法則を表す式の四つの微分方程式からなる。マクスウェルが1864年に提出。電磁方程式。

出典　小学館

精選版 日本国語大辞典

マクスウェル の 方程式(ほうていしき)

1. 電磁気学の基礎方程式。方程式は電磁誘導を表わす式、電流と変位電流による磁気作用を表わす式、および補足条件を表わす二式の合計四つの式から成る。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

マクスウェルの方程式 (マクスウェルのほうていしき)
Maxwell's equations

電磁気学の基礎方程式。J.C.マクスウェルが，それまでに知られていた，いくつかの電磁現象を四つの簡単な方程式にまとめあげて表現したもので，後にH.ヘルツによって発展させられたのでマクスウェル=ヘルツの電磁方程式とも呼ばれる。これらの方程式は積分形で表現されることもあるが，微分方程式の形で表現されているものを指すのがふつうである。電場，磁場，電荷，電流など電磁気学の諸量の間の関係が，時間を含めた四次元時空の各点で成立するように表現できた点では画期的なものといえる。以下，その四つの方程式を説明する。

（1）ある線輪を貫いている磁力線の数が時間的に変化すると，その変化の速さに比例した起電力がこの線輪に生ずることは，M.ファラデーの電磁誘導の法則として知られていた。マクスウェルは，この関係は別に線輪などはなくても，電磁気学的場の中にある任意の閉曲線について成立するものであると解釈を拡張した。任意の閉曲線Cに沿って電場Eを線積分した値は，Cで囲まれた面積Sを貫いている磁束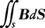（Bは磁束密度）の時間変化に等しいとすることである。すなわち，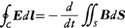

この式に数学のストークスの定理を適用すると，

が得られる。ここでrotはベクトルEからその循環を表すベクトルをつくりだす空間微分演算子である（回転）。（1）は空間の各点で電場と磁場の時間および空間微分について成立する関係で，ファラデーの電磁誘導の法則よりはるかに広い意味をもっている。

（2）A.M.アンペールは電流の間に力が働くことを見いだしたが，これは電流もその周囲に場をつくっているからであると考えられる。これが磁場に相当し，場の量を使ってこれを表現すると，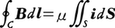

となる。iは閉曲線C内を流れる電流の密度，μは透磁率である。この式に再びストークスの定理を用いると，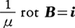

が得られる。マクスウェルは磁場B/μをつくる原因として，この電流iのほかに，電場の時間的変化もありうるとして，ε（∂E/∂t）の項をつけ加え（εは誘電率），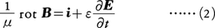

の方程式をたてた。ε（∂E/∂t）の項は，変位電流と呼ばれる。（2）と（1）とでは電場と磁場の役割が交換された関係になっているが，当時はこの変位電流の項の存在を直接示唆する実験的証拠はなかった。しかしこの項は電磁波の存在を導くなど，重要な発見であり，その後の理論的・実験的検討からも，ゆるぎない事実として受け入れられている。

（3）電荷分布ρ（r′）が電場E（r）をつくるというクーロンの法則，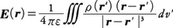

にガウスの法則を適用し，微分形で表現すると，

が得られる。

（4）また任意の閉曲面上で磁場を測りその値を閉曲面Sについて積分すると，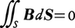

となる事実が得られるが，この式にもガウスの定理を適用すると，

　divB＝0　……（4）　

が得られる。また（4）は，磁荷は存在しないという一つの表現にもなっている。

　ふつう（1），（2），（3），（4）の四つの式を合わせてマクスウェルの方程式と呼ぶ。なかでも（1），（2）は電場，磁場の間の相互的因果関係を表していて，とくに重要な式である。マクスウェルの方程式はすべての電磁現象の基本となっている。しかも時空の1階微分量の間の線形的関係で表現されているという特徴をもっている。
執筆者：清水 忠雄

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

マクスウェルの方程式
マクスウェルのほうていしき
Maxwell's equation

電磁気現象を支配する基礎方程式。 J.C.マクスウェルは電磁気に関する諸法則を次の1組の基礎方程式に定式化した。
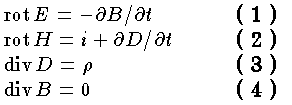ここで E は電場，H は磁場，D は電束密度，B は磁束密度，i は電流密度，ρは電荷密度，t は時間を表わす。 (1) 式は電磁誘導の法則，(2) 式は電流のつくる磁場に関するアンペールの法則を変位電流 ∂D/∂t を加えて一般化したもの。この2つの式で電場と磁場が関係づけられ，これにクーロンの法則に由来する (3) ，(4) 式が補足されている。 (3) ，(4) 式はもともと定常状態で導かれたものであるが，非定常状態においても成り立つと考えられた。等方性の媒質中では，誘電率をε，透磁率をμとすれば，D＝εE ，B＝μH である。 (2) 式で変位電流 ∂D/∂t をつけ加えたのは電荷の保存についての連続の式 divi＝－∂ρ/∂t を考慮したからである。変位電流を導入したことによりマクスウェルはこの基礎方程式から電磁波の存在を理論的に予言したが，これは数年後 H.R.ヘルツにより実験的に証明された。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

マクスウェルの方程式
まくすうぇるのほうていしき
Maxwell's equations

電磁場の時間的、空間的変化を記述するもっとも基本的な方程式である。1864年にイギリスのマクスウェルによって提出されたので、この名でよばれるが、それ以前の多数の実験家によって得られたいくつかの実験事実に基づいている。ドイツのH・R・ヘルツが発展させたので、マクスウェル‐ヘルツの電磁方程式Maxwell-Hertz's electromagnetic equationsともいう。自然界におけるほとんどの電磁気現象は、この方程式から出発して説明できる。古典的電磁気現象に関しては完全であるが、量子力学的現象が関与してくる現象においては完全ではなくなる場合がある。物質中においては、量子力学的現象が関与してくるが、現象を巨視的にとらえる場合には物質中でも成り立つように拡張されたマクスウェルの方程式を適用することができる。

　マクスウェルの方程式は次の4個の方程式から成り立っている。

　　rotE=∂B/∂t……(1)
　　rotH=(∂D/∂t)+i……(2)
　　divD=ρ……(3)
　　divB=0……(4)
ここで、Eは電場、Bは磁束密度である。EとBはローレンツ力によって定義される。iは電流密度である。DはEを使って定義されるが、物質中においては物質の電気的性質に依存する。一般にD=εEと書いてεをその物質の誘電率とよぶ。HはBを使って定義されるが、物質中においては物質の磁気的性質に依存する。一般にB=μHと書いてμをその物質の透磁率とよぶ。マクスウェルの方程式のうち(3)と(4)は、それぞれ(2)と(1)に対する初期条件の意味をもっている。こうして6個の未知関数EとBに対して、時間的変化を記述する6個の方程式が与えられていることになる。

［安岡弘志］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

マクスウェルの方程式【マクスウェルのほうていしき】

電磁場の性質を記述する基本的な微分方程式。マクスウェルが定立，H.ヘルツがさらに発展させたもので，電磁気学の基礎をなす。電場の強さ，磁場の強さ，電流密度，電束密度，磁束密度の各ベクトルをE，H，I，D，B，電荷密度をρとすると，単位系によって表現に差があるが，MKSA単位系では，rotE＝∂B/∂trotH＝∂D/∂t＋IdivD＝ρdivB＝０rotは回転，divは発散の記号。上式は順に，電磁誘導，電流の磁気作用，静電場，静磁場の諸現象を表す。
→関連項目電気力学｜ローレンツ変換

出典　株式会社平凡社

法則の辞典

マクスウェルの方程式【Maxwell's equation】

「マクスウェルの粘弾性の方程式」ともいう．粘弾性体においては，応力の時間変化は，完全弾性体におけるフックの法則＊で表される項に，応力が時間とともに減少していく項を付加する必要がある．したがって

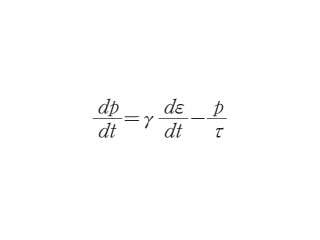
のようになる．ここで γ はフックの法則における弾性率，p は応力，τ は緩和時間を表す．

この式は，別名を「マクスウェルの微分方程式」ということもあるが，フォークトの式＊と並んで粘弾性の基礎方程式である．

マクスウェルの方程式【Maxwell's equation】

「マクスウェル‐ヘルツの電磁方程式」のページをご覧ください。

マクスウェルの方程式【Maxwell's equations】

「マクスウェルの熱力学方程式」のページをご覧ください。

出典　朝倉書店

世界大百科事典（旧版）内のマクスウェルの方程式の言及

【電磁気学】より

…電流は電荷の運動の集りであるから，電流が磁場から受ける力は上のローレンツ力から導かれる。
［マクスウェルの方程式］
　前述の(1)に答えるのがマクスウェルの方程式である。これは電場，磁場の時間的および空間的変化を，電荷と電流の分布から定める式で，それまでに知られていた電磁気学の法則をマクスウェルが集大成し，一般化したものである。…

【マクスウェル】より

…このとき用いたアナロジーの手法には師であるG.G.ストークスの流体力学の研究成果も役だった。《ファラデーの力線について》(1856)，《物理的力線について》(1861‐62)，《電磁場の動力学理論》(1864)の三つの論文で，今日〈マクスウェルの方程式〉と呼ばれる電磁場の基本方程式を導出し，この中で変位電流という新しい概念を提案して電磁作用が空間を伝搬する可能性を検討し，光が電磁波であることを推論した。これらの成果を集大成した《電磁気学Treatise on Electricity and Magnetism》(1873)は物理学史上の画期を成した。…

※「マクスウェルの方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」