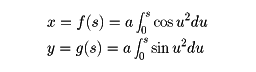クロソイド（読み）くろそいど（英語表記）clothoid

デジタル大辞泉

クロソイド（clothoid）

螺線らせんの一。曲線の長さと曲率半径とが逆比例する、渦巻き形の曲線。1744年オイラーが発見、M＝コルニュが物理光学の回折現象の幾何学的表現として用いた。コルニュの螺線。

出典　小学館

改訂新版　世界大百科事典

クロソイド
clothoid

フレネル積分，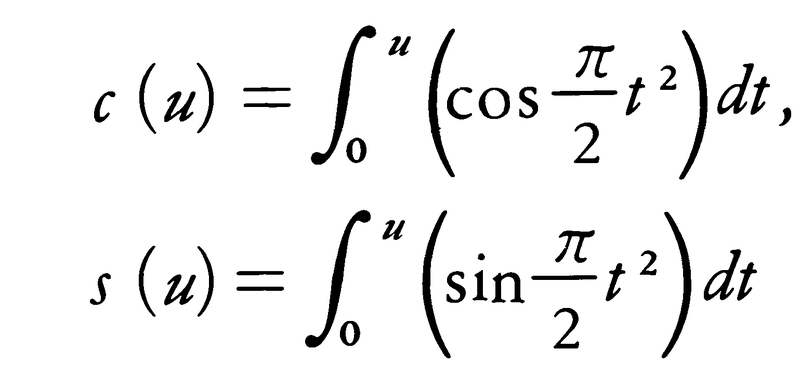

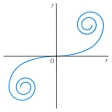
を考えるとき，媒介変数uを用いて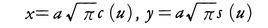，で表される曲線をクロソイドという。弧長がsである点における曲率がa²/sである曲線はクロソイドの一部をなす。コルニュM.A.Cornu（1841-1902）が，物理光学における回折現象の表現のためにこの曲線を用いたので〈コルニュの螺旋〉とも呼ばれる。一定の速さで走る車のハンドルを一定の角速度で回転したとき，この車の走る道筋はこの曲線になる。そのためこの曲線の一部が高速道路などに応用される。
執筆者：中岡 稔

図－クロソイド

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

クロソイド
くろそいど
clothoid

平面曲線の一つ。コルニュCornuの螺線(らせん)ともよばれる。これは、媒介変数sを使って、

で表される。このとき、sは原点から測った曲線の長さであり、その点における曲率半径をρとすれば、ρs＝2aという関係がある。

　この曲線上を定速で走る車については、進行方向の変化率が一定となるので、運転者はハンドルを一定の角速度で回せばよい。このため、この曲線は高速道路のカーブの所の曲線として、しばしば用いられる。

［竹之内脩］

クロソイド

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

クロソイド
clothoid

オイラーのスパイラル，コルニュのスパイラルともいう。 L.オイラーによって発見され (1744) ，また M.コルニュ (1841～1902) が光学における回折現象を幾何学的に表現するために用いた曲線で， sin (x²) ， cos (x²) の積分値を座標とする曲線である。この曲線は，その曲率変化の性質から，高速道路のカーブをつける場合にも利用される。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

クロソイド

らせん曲線の一つ。曲線上の任意の点でそこの曲率半径（曲率）と原点よりの曲線長の積が一定の曲線。一定の速さで走る自動車が，ハンドルを一定速度で回転して進んだときの走行軌跡がこの曲線。緩和曲線としてこの曲線の一部が高速道路等に使用。
→関連項目高速道路

出典　株式会社平凡社

世界大百科事典（旧版）内のクロソイドの言及

【曲線】より

…とくに，r＝aθ,r＝ae^bθ,r＝a/θ(a,bは定数)で表される曲線をそれぞれアルキメデスの螺線Archimedes’ spiral，対数螺線logarithmic spiral(等角螺線equiangular spiral)，双曲螺線hyperbolic spiralという(図21)。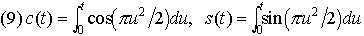とおくとき，tを媒介変数として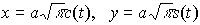，で表される曲線をコルニュの螺線Cornu’s spiralまたはクロソイドclothoidという(図22)。【中岡 稔】。…

【曲線】より

…とくに，r＝aθ,r＝ae^bθ,r＝a/θ(a,bは定数)で表される曲線をそれぞれアルキメデスの螺線Archimedes’ spiral，対数螺線logarithmic spiral(等角螺線equiangular spiral)，双曲螺線hyperbolic spiralという(図21)。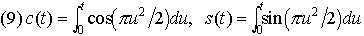とおくとき，tを媒介変数として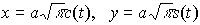，で表される曲線をコルニュの螺線Cornu’s spiralまたはクロソイドclothoidという(図22)。【中岡 稔】。…

【高速道路】より

…(3)線形　高速道路の線形は，自動車の高速連続走行に適するように，連続的で流れるような形に設計される。平面線形は，一般に直線，円，クロソイドの3要素で構成され，曲率の徐々に変わるらせん形の一種であるクロソイドを，補助的にではなく，円，直線と並ぶ主要線形要素として用いることによって，視覚的にも滑らかで運転しやすく，また地形になじみ，経済的で自然環境を損なうことの少ない道路が作られている。円曲線の最小限度は設計速度によって定められ100km/hでは，特別の場合を除いて最小半径460mである。…

【螺旋(螺線)】より

…(d)方程式r²θ＝a²(aは定数)で表される曲線はリチュスと呼ばれる(図4)。(e)方程式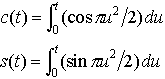，とおくとき，直交座標系に関して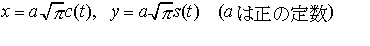，と媒介変数表示される曲線をコルニュの螺線またはクロソイドという。弧長がsである点における曲率がa²/sである平面曲線はコルニュの螺線の一部である。…

※「クロソイド」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」