螺旋（読み）ラセン

デジタル大辞泉

ら‐せん【^×螺旋】

１ 巻き貝の殻のようにぐるぐると巻いているもの。「螺旋を描く」「螺旋状」「螺旋形」
２ 「螺子ねじ」に同じ。
[補説]書名別項。→らせん
[類語]渦・渦巻き・とぐろ

らせん［書名］

鈴木光司のホラー小説。「リング」の続編に当たる。平成7年（1995）刊行。平成8年（1996）第17回吉川英治文学新人賞受賞。平成10年（1998）飯田譲治監督により映画化。テレビドラマや漫画化作品もある。

出典　小学館

精選版 日本国語大辞典

ら‐せん【螺旋】

1. 〘 名詞 〙
2. ① 巻き貝の殻の線のようにぐるぐる回った筋。また、そのような構造。
   1. [初出の実例]「龍尾車は河浜にて水を引揚るの器なり、〈略〉此のもの内に螺旋の孔道あり」(出典：成形図説（1804‐06）一二（古事類苑・産業一）)
3. ② ＝らせん（螺線）②
   1. [初出の実例]「夫を螺旋(ラセン)の締棒の下に押込んで、把をぐるぐると廻し始める」(出典：満韓ところどころ（1909）〈夏目漱石〉一七)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

螺旋（線） (らせん)

〈螺〉はすなわち巻貝の殻のことで，巻貝の殻のようにぐるぐるとねじれた形態の総称。この語は，渦，ねじを含めて多様なものを指すので，まず幾何学的な整理が必要である。

数学におけるらせん

幾何学的におけるらせんには平面曲線と空間曲線の二つがある。

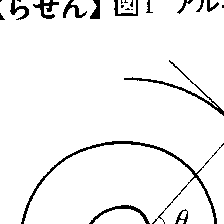
（1）螺線spiral　1点のまわりをぐるぐるまわる平面曲線を総称して螺線，渦巻線，スパイラルなどと呼ぶ。その多くは，極座標（r，θ）を用いて，方程式r＝f（θ）（fは単調関数）の形で表される。次にその代表例を五つあげておく。（a）方程式r＝aθ（aは正の定数）で表される曲線，すなわち半直線が点Oのまわりを一様な速さで回転し，同時に点Pがこの半直線上をOから一様な速さで遠ざかるときに点Pの描く曲線は，その接線と面積を詳しく調べたアルキメデスにちなんで，アルキメデスの螺線と呼ばれる（図1）。動径OPとPにおけるこの曲線の接線とのなす角をαとすればtanα＝θで，したがってθ→∞ならばα→π/2となる。（b）方程式r＝a/θ（aは正の定数）で表される曲線を双曲螺線という（図2）。この曲線は原線と平行で原線との距離がaである一つの直線を漸近線にもつ。（c）方程式r＝ke^aθ（k，aは正の定数）で表される曲線を対数螺線と呼ぶ（図3）。動径とその端におけるこの曲線の接線とのなす角は一定であるので，この曲線はまた等角螺線とも呼ばれる。さらに，この曲線の伸開線，縮閉線はともに元の曲線に合同であることを発見したヨハン・ベルヌーイ（1667-1748）にちなんで，この曲線はベルヌーイの螺線とも呼ばれる。弧長がsである点における曲率がas＋b（a，bは定数，a≠0）である平面曲線は対数螺線である。（d）方程式r²θ＝a²（aは定数）で表される曲線はリチュスと呼ばれる（図4）。（e）方程式，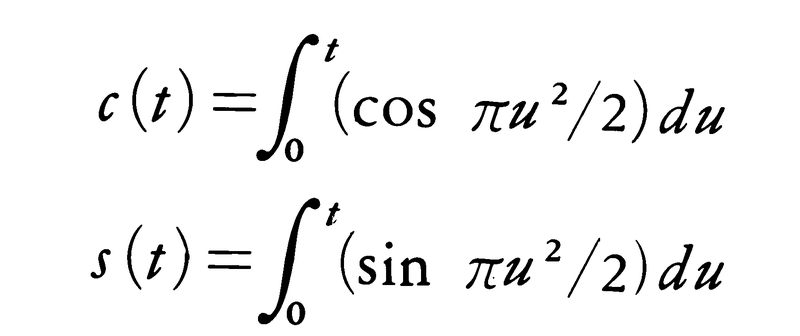

とおくとき，直交座標系に関して，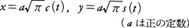

と媒介変数表示される曲線をコルニュの螺線またはクロソイドという。弧長がsである点における曲率がa²/sである平面曲線はコルニュの螺線の一部である。

（2）螺旋helix　ヘリックスともいう。直円柱の母線を一定の角度で切る空間曲線を常螺旋またはつる巻き線という（図5）。直円柱の底面の半径がaで，一定の角度がαであれば，直円柱の軸をz軸とする直交座標系に関して，常螺旋はx＝a cos t，y＝εa sin t，z＝at tan α（ε＝±1）と媒介変数表示される。常螺旋はその上の各点における曲率および捩れ率が点のとり方によらず一定（≠0）であるような曲線ということができる。常螺旋の主法線はそれがのる直円柱の軸に直交する。常螺旋の主法線の描く曲面を常螺旋面という（図6）。空間曲線上の各点における接線がつねに一定方向と定角をなすとき，この曲線を一般螺旋または定傾曲線という。一般螺旋はその上の各点における曲率と捩れ率の比が点のとり方によらず一定であるような曲線ということができる。一つの曲線が1直線のまわりを一定の角速度で回転しながらその直線の方向に一定の速度で移動するときにできる曲面を螺旋面という。
執筆者：中岡 稔

自然界におけるらせん

人工物および流体における各種の渦を除けば，自然界におけるらせんはほとんど生命と結びついている。平面曲線としての螺線は，動物では巻貝の殻，牛や羊の角，象の牙や齧歯（げつし）類の門歯，毛の巻き（つむじ），植物では集散花序のうちのかたつむり花序，シダ植物の若い芽の先端などさまざまのものが見られる。貝殻や角や牙など，硬くて段階的に成長していく器官は典型的な対数螺線であり，成長につれて大きさの異なる相似の形態がつけ加わることによってでき上がる。巻いた象の鼻やカメレオンの尾も対数螺線であるが，こちらはもともと円錐状のものを巻くことによってできたものである。これに対して，蛇の体や体毛のように太さの一様なものが巻けばつる巻き線ができる。一般にこの種の平面螺線は成長部における成長速度の不均衡の結果として形成される。

　空間曲線としての螺旋は，その構造上の支持性，安定性が多くの生物で利用されている。植物のつるや猿の尾，ネコザメの卵殻などに見られるように，このらせんは他物にからみつく場合に強力な支持体となる。らせんどうしがからみあって二重，三重になれば，その安定性，強度は非常に高まる。これは縄やロープと同じ原理であるが，生体内にもDNAの二重らせん，ペプチドのα-らせん，各種のタンパク質，染色体のヌクレオソーム構造の多重らせんなど多くのらせん構造が見られる。

　螺旋平面の実例としては，らせん階段などがあるが，われわれの日常生活にもっともかかわりの深いのはねじである。生物でもリスやムササビの陰茎はねじ状になっており，生殖器官としての適応性を高めている。

　らせんを圧縮すればばねになる。つまり平面曲線の場合は渦巻ばねいわゆる〈ぜんまい〉に，空間曲線の場合はコイルばねないしつる巻きばねになる。ばねの力を生かした生物の構造としては刺胞動物の刺糸がある。

　一方，らせん構造は限られた容積の中で表面積を大きくすることが可能なので，軟骨魚類の結腸内部のらせん弁，オタマジャクシの腸などでは吸収表面積の拡大に利用されている。電熱器のニクロムコイルや電球のフィラメントなども同じ原理によっている。またこれは逆にいえば長いものを小さく折りたたむのに適した構造ともいえるわけで，チョウやガがみつを吸うときの口吻（こうふん）はその典型的な構造である。

　なお，らせんには左巻き，右巻きの問題がつきまとうが，それについては〈右と左〉の項目を参照されたい。
執筆者：森 三男

シンボリズム

らせんは，一般的にいって宇宙の誕生と進化にかかわる象徴的図形であり，成長，上昇と下降，統合と多様化，収縮と拡張などを意味する。渦巻形など類似の図形と同様，右回りと左回りが対照的な意味をになうことが多い。ギリシアでは右回りのらせんはアテナ神の属性で創造的，前進的であり，その反対の左回りのらせんはポセイドン神の属性とされ，竜巻や海の渦のように破壊的，退行的なものと考えられていた。またエジプトのトート神は，しばしば手にらせん状のものをもっていたり，頭上に渦巻状のものをつけているが，これは霊魂や生命の息吹を示すものといわれる。らせんはまたしばしば杖（つえ）にからむ蛇の形であらわされ，生命力，権威などの力の象徴である。ギリシアの医療神アスクレピオスのもつ杖や，ヘルメス神の持物のカドゥケウスにおける二重の蛇の螺旋は，いずれも超自然的な力を示す。インドのヨーガにおける性力（シャクティ）の根源であるクンダリニーも同様の表象といえよう。またらせんは迷路の象徴的主題ともかかわり，本能的な力，母の子宮への退行，または中心への道を表す図形として，天国や聖地への巡礼路を示すこともある。
執筆者：秋山 さと子

図1～図6

出典　株式会社平凡社「改訂新版　世界大百科事典」

普及版 字通

【螺旋】らせん

うずまきにまく。〔大唐西域記、一、畢試国〕如來(によらい)の髮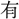り。髮の色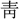紺、螺旋して右に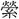(めぐ)る。引けば長さ尺餘、卷けば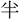寸可(ばかり)なり。

字通「螺」の項目を見る。

出典　平凡社「普及版 字通」

百科事典マイペディア

螺旋(螺線)【らせん】

（１）渦巻線とも。極座標でr＝f（θ）（fは単調連続関数）と表される平面曲線。r＝aθ（aは正の定数）で表されるアルキメデスの螺線，r＝ke(a/)θの対数螺線，r＝a/θの双曲螺線等がある。（２）つるまき線とも。直円柱の側面に含まれる空間曲線で円柱の母線と一定角度で交わるものを常螺旋という。tを媒介変数としてx＝acos t，y＝asin t，z＝bt（a，bは定数）で表される。

出典　株式会社平凡社

世界大百科事典（旧版）内の螺旋の言及

【曲線】より

…通俗には直線でない線を曲線と呼び，数学の古典であるユークリッドの《ストイケイア》もこの立場をとっている。しかしながら，現今の数学では曲線は線の同義語で，直線をもその中に含める。ユークリッドは〈線とは幅のない長さで，その端は点である〉と述べ，線すなわち曲線の一応の説明をしている。しかしこれは完全な定義とはいえない。ユークリッド以後は19世紀後半まで，曲線は自明な概念として定義も与えられず使われてきたが，今日では曲線を解析的表示によって定義する。…

※「螺旋」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」